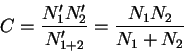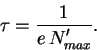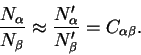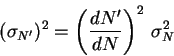|
Астронет: А. В. Миронов/ГАИШ Прецизионная фотометрия http://www.astronet.ru/db/msg/1169494/node43.html |
<< 6.1 Журнал наблюдений | Оглавление | 6.3 Учет атмосферной экстинкции >>
- 6.2.1 Лабораторный метод суммы потоков
- 6.2.2 Mетод максимума сигнала
- 6.2.3 Метод диафрагмирования главного зеркала
- 6.2.4 Метод поиска отклонений от пуассоновского распределения.
6.2 Учет нелинейности в методе счета фотонов
Первое, что нужно сделать при редукциях - это учесть нелинейность. При
работе с усилителями постоянного тока этот вопрос довольно сложен.
Остановимся на порядке учета нелинейности при измерениях по методу
счета фотонов. В гл. III для учета этого эффекта мы получили формулы
(3.9), и (3.11). Задача только в том, чтобы
определить величину параметра ``мертвого времени'' ![]() . Это можно
сделать разными методами.
. Это можно
сделать разными методами.
6.2.1 Лабораторный метод суммы потоков
При испытаниях фотоумножителей в лабораторных условиях
несложно определить параметр ![]() , имея специально
сконструированный осветитель. В этом осветителе имеется два
источника света и есть возможность освещать фотокатод ФЭУ либо
одним источником, либо вторым, либо двумя вместе. Разумеется,
нужно позаботиться о том, чтобы за время измерений освещенность,
создаваемая каждым из источников была постоянной.
, имея специально
сконструированный осветитель. В этом осветителе имеется два
источника света и есть возможность освещать фотокатод ФЭУ либо
одним источником, либо вторым, либо двумя вместе. Разумеется,
нужно позаботиться о том, чтобы за время измерений освещенность,
создаваемая каждым из источников была постоянной.
Пусть на первый источник ФЭУ реагирует выдачей сигнала
![]() имп/с, а на второй, соответственно,
имп/с, а на второй, соответственно, ![]() имп/с.
Из формулы (3.6) следует:
имп/с.
Из формулы (3.6) следует:
Если осветить ФЭУ суммарным светом двух источников, то зарегистрированному отсчету
Три уравнения (6.1), (6.2) и (6.3) образуют систему с тремя неизвестными
не зависит от значения
6.2.2 Mетод максимума сигнала
Продифференцируем обе части формулы (3.6) по ![]() . Получим
. Получим
При увеличении освещенности фотокатода ФЭУ сначала отсчеты
растут, затем этот рост замедляется и, наконец, отсчеты начинают
уменьшаться. Если зарегистрировать этот максимум, то
6.2.3 Метод диафрагмирования главного зеркала
Когда ваш фотометр висит на телескопе, лабораторные методы
неудобны. Нужно уметь контролировать ![]() по звездам, не снимая
аппаратуру. Для этого в районе зенита выбираются две близкие по
расположению звезды (чтобы атмосфера влияла на них одинаково),
различающиеся по звездной величине на
по звездам, не снимая
аппаратуру. Для этого в районе зенита выбираются две близкие по
расположению звезды (чтобы атмосфера влияла на них одинаково),
различающиеся по звездной величине на ![]() -
-![]() . Обычно стараются
подобрать звезды одинакового спектрального класса, или наблюдают
их через узкополосный светофильтр.
. Обычно стараются
подобрать звезды одинакового спектрального класса, или наблюдают
их через узкополосный светофильтр.
Несущественно, во сколько раз будут различаться потоки от них, но существенно, что при различных значениях апертуры телескопа отношение их внеатмосферных потоков есть постоянная величина. Изменять апертуру можно разными способами. Например, у телескопов АЗТ-14 есть очень удобное устройство: ирисовая диафрагма на главном зеркале. При разных раскрытиях диафрагмы вы получите разный поток от обеих звезд.
Обозначим две выбранные звезды буквами ![]() и
и ![]() . Заметим, что
при малых раскрытиях диафрагмы потоки будут малы, и нелинейность
практически не будет влиять на отсчеты и при этом можно измерить
истинное отношение потоков от двух звезд
. Заметим, что
при малых раскрытиях диафрагмы потоки будут малы, и нелинейность
практически не будет влиять на отсчеты и при этом можно измерить
истинное отношение потоков от двух звезд
Уравнения (6.7), (6.8) и (6.9) составляют систему с тремя неизвестными, решая которую получаем значение
6.2.4 Метод поиска отклонений от пуассоновского распределения.
Нетрадиционный метод определения ![]() был выдвинут
В.Г.Корниловым. Представим, что мы получили большое количество
измерений постоянного светового потока. Эффект нелинейности
искажает не только измеренную среднюю величину, но и другие
статистические характеристики, в частности дисперсию. Дисперсия
реально регистрируемого числа импульсов связана с дисперсией для
идеально линейной приемной аппаратуры следующим соотношением:
был выдвинут
В.Г.Корниловым. Представим, что мы получили большое количество
измерений постоянного светового потока. Эффект нелинейности
искажает не только измеренную среднюю величину, но и другие
статистические характеристики, в частности дисперсию. Дисперсия
реально регистрируемого числа импульсов связана с дисперсией для
идеально линейной приемной аппаратуры следующим соотношением:
или
Уравнение (6.12) в сочетании с уравнением (3.11) решается численно одним из итерационных методов. Метод удобен, если регистрация результатов измерений производится с помощью ЭВМ.
<< 6.1 Журнал наблюдений | Оглавление | 6.3 Учет атмосферной экстинкции >>