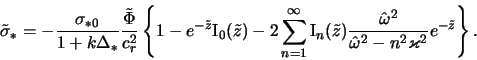 |
Астронет: А. Г. Морозов, А. В. Хоперсков Физика Дисков http://variable-stars.ru/db/msg/1168623/node36.html |
<< 6.1 Возбуждение грав. волн плотности | Оглавление | 6.3 Сложные спиральные узоры >>
6.2 Гидродинамическая концепция образования спиральной структуры
На протяжении этой книги не раз упоминалось о гидродинамической концепции образования спиральных структур плоских галактик. Согласно этой концепции, предложенной А.М. Фридманом в 1972 г., спиральные рукава представляют собой волны плотности, нарастающие до нелинейных амплитуд из-за развития гидродинамических (неджинсовских) неустойчивостей в газовом галактическом диске. Различным аспектам этой концепции посвящен ряд обзорных статей и монографий [2,354,503-505].
В основе этой концепции лежит следующий факт. Газовый диск
галактики, как правило, обладает массой, много меньшей массы
звездного диска (см. п. 1.2.1) и, следовательно,
. Из этого,
казалось бы, должен следовать вывод, что газ не вносит заметного
вклада в гравитационный потенциал. Это справедливо для
осесимметричных моделей. Однако необходимо учитывать, что в
бесстолкновительной плазме звезд везде, кроме центральных
областей 
галактик, амплитуда плотности неосесимметричных
особенностей значительно меньше полной плотности звездного диска
(
), тогда как в силу
столкновительности газа
распространяющиеся в нем возмущения плотности могут достигать
значительных амплитуд
(значком
" 
" помечены возмущенные
величины). Если значения величин 
и
составляют несколько
процентов от 
, то возможна ситуация
, или даже
(см. [349,504]).
Пусть в газовом диске возникло возмущение плотности. Для
оценок (см. подробнее работу Фридмана [349]) воспользуемся
выражением (4.2.11)
для возмущенного гравитационного потенциала с
учетом конечной толщины газового диска
Принимая во внимание условие
, которое выполняется для
Галактики [349], можно для оценок принять
.
Последнее соотношение совместно с (6.2.1) дает
В окрестности Солнца для длины волны спирального узора
кпк и значений
M
/пк
, 
км/с, 
пк,
пк получаем
В области внутреннего максимума на кривой вращения (
кпк)
это отношение оказывается еще меньше [349]. Как видим, при
исследовании гидродинамических механизмов генерации спиральной
структуры можно в первом приближении не учитывать возмущение
звездной подсистемы.
Наиболее вероятным претендентом на роль генератора спиральной структуры (по времени развития и параметрам возникающих спиралей в рамках линейного анализа) среди гидродинамических неустойчивостей является центробежная. Эта неустойчивость возбуждается в области отрицательного градиента скорости в галактиках с двугорбыми кривыми вращения (в разд. 4.5 в рамках различных моделей подробно проанализированы условия возникновения центробежной неустойчивости и свойства возникающего спирального узора).
Обсуждаемая здесь проблема допускает уникальную возможность лабораторного моделирования ("галактика на кухонном столе"). Незлин и Снежкин [505] подробно описали как методику экспериментов на установке с вращающейся "мелкой водой", так и результаты. Поэтому ниже мы кратко остановимся только на основных моментах.
В основе возможности лабораторного моделирования спирального
галактического узора лежит эквивалентность систем уравнений,
описывающих динамику обширных центральных областей газовых дисков
плоских галактик и тонкого слоя вращающейся несжимаемой жидкости.
При этом толщина слоя жидкости 
соответствует поверхностной
плотности сжимаемого газа, а роль скорости звука в газе играет
характерная скорость волн на мелкой воде
[327].
Для моделирования двугорбой кривой вращения ("скачка" скорости)
можно использовать два параболоида, вращающихся с различной
угловой скоростью. Проведенные опыты показали, что развитие
неустойчивости приводит к возникновению спиральных волн
поверхностной плотности различных азимутальных мод (
). Спирали являются отстающими. Вращение спирального
узора происходит со скоростью, промежуточной между скоростями
вращения центральной части и периферии. Для определенной моды
угловая скорость вращения спирального узора 
является монотонно
возрастающей функцией от числа Маха (рис. 6.5). Каждая мода может
существовать только в определенном диапазоне параметров. Так, в
условиях рис. 6.5 моды 
могут реализоваться, если
число Маха не превышает значений соответственно
. Когда при плавном увеличении 
система проходит через
эти границы, наблюдается перестройка данной моды в более
крупномасштабную (
уменьшается). Перестройка мод является
существенно нелинейным процессом -- это видно уже из того, что
переходы между модами имеют скачкообразный и гистерезисный
характер. Общая закономерность заключается в том, что число
спиралей на периметре системы уменьшается при увеличении числа .
Сравнение результатов лабораторных экспериментов с выводами
линейной теории (речь не идет, разумеется, об амплитуде)
свидетельствует о различиях, не превышающих 30%.
 |
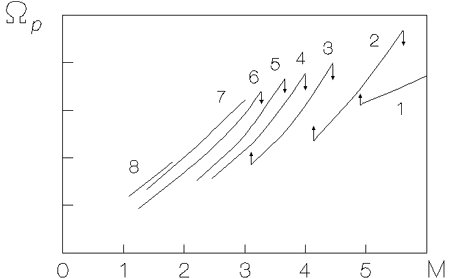Рис. 6.5. Угловая скорость
вращения спирального узора
|
Помимо центробежной неустойчивости в рамках
гидродинамической концепции исследуются и другие. Между краем
центрального молекулярного диска и особенностью на кривой
вращения (излом или скачок) образуется волноводный слой, в
котором могут "раскачиваться" неустойчивости резонансного типа,
аналогичные обсуждавшимся в разд. 5.3 [506]. Другой возможный
механизм -- резонансно-центробежный, обсуждается в разд. 4.5 и
6.3. К появлению крупномасштабного спирального узора должно
приводить и развитие мод неустойчивости Папалойзу-Прингла с
низшими азимутальными номерами 
даже в диске без
особенностей на кривой вращения (см. п. 5.3.3). Предлагались и
другие гидродинамические механизмы [507].
<< 6.1 Возбуждение грав. волн плотности | Оглавление | 6.3 Сложные спиральные узоры >>