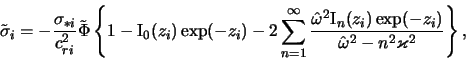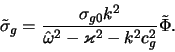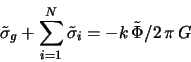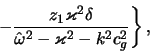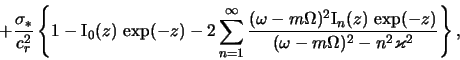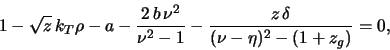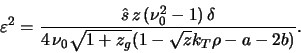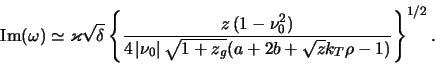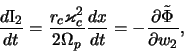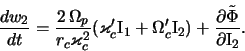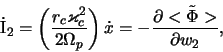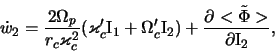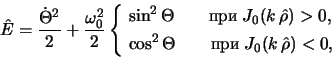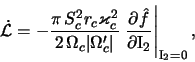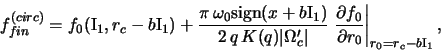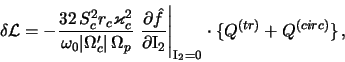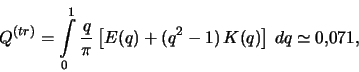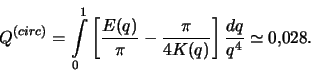|
Астронет: А. Г. Морозов, А. В. Хоперсков Физика Дисков http://www.astronet.ru/db/msg/1168623/node35.html |
<< 6. Природа спирального узора | Оглавление | 6.2 Гидродинамическая концепция ... >>
- 6.1.1 Механизм гравитационной неустойчивости на периферии богатого газом диска
- 6.1.2 Роль звездообразования
- 6.1.3 Резонанс радиального потока газа с гравитационной спиральной волной
- 6.1.4 Нелинейное насыщение резонансного усиления спиральных волн на коротационном радиусе
6.1 Проблемы возбуждения гравитационных волн плотности
6.1.1 Механизм гравитационной неустойчивости на периферии богатого газом диска
Население дисков галактик неоднородно по своим динамическим характеристикам -- парциальным вкладам в полную поверхностную плотность диска и дисперсиям скоростей составляющих его объектов. Так, подсистемы довольно молодых звезд ранних спектральных классов (O, B, A) характеризуются малой поверхностной плотностью и малыми дисперсиями скоростей, в то время как подсистемы старых звезд гораздо более массивны и дисперсии их радиальных скоростей велики [53]. Относительный же вклад газовой подсистемы в полную плотность диска растет с удалением от центра при практически постоянной дисперсии скоростей газовых облаков (много меньшей дисперсии скоростей старых звезд).
Исследуем динамику малых возмущений гравитационного типа в
плоскости такого многокомпонентного диска, пренебрегая в первом
приближении радиальной неоднородностью его равновесных параметров
(![]() , где
, где ![]() -- волновое число,
-- волновое число, ![]() -- масштаб радиальной
неоднородности диска). Это
приближение позволяет исключить из рассмотрения ветви
градиентного типа и тем самым изучить независимо важные для теории
Лина и Шу [196,197] дисперсионные свойства гравитационных
спиральных волн плотности.
Эта задача была впервые поставлена Лином
и Шу [197] (ими был исследован двухкомпонентный звездно-газовый
диск с
-- масштаб радиальной
неоднородности диска). Это
приближение позволяет исключить из рассмотрения ветви
градиентного типа и тем самым изучить независимо важные для теории
Лина и Шу [196,197] дисперсионные свойства гравитационных
спиральных волн плотности.
Эта задача была впервые поставлена Лином
и Шу [197] (ими был исследован двухкомпонентный звездно-газовый
диск с
![]() ), а излагаемые ниже
результаты получены в [486].
), а излагаемые ниже
результаты получены в [486].
Равновесные функции распределения звезд полагаем
шварцшильдовскими (см. п. 2.1.2) с парциальными
поверхностными плотностями звездных подсистем
![]()
![]() и соответствующими дисперсиями радиальных
скоростей
и соответствующими дисперсиями радиальных
скоростей ![]() . Газовую подсистему характеризуем аналогичными
параметрами
. Газовую подсистему характеризуем аналогичными
параметрами ![]() ,
, ![]() . В принятом приближении возмущенная плотность
. В принятом приближении возмущенная плотность
![]() -й звездной подсистемы
-й звездной подсистемы
![]() связана с возмущенным
гравитационным потенциалом
связана с возмущенным
гравитационным потенциалом ![]() соотношением (см. п. 2.2.2)
соотношением (см. п. 2.2.2)
Подставляя затем в уравнение Пуассона для многокомпонентного диска
выражения (6.1.1), (6.1.2), получим искомое дисперсионное уравнение
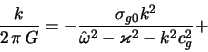
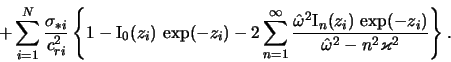
Дальнейший анализ проведем в рамках модели двухкомпонентного звездного диска
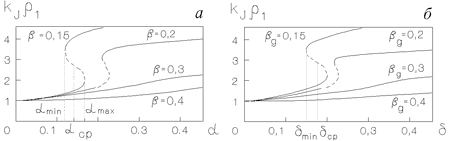 |
Рис. 6.1. Зависимость обратного
джинсовского масштаба |
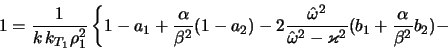
где
Граница гравитационной устойчивости рассматриваемой модели
диска определяется из условия
![]() в минимуме дисперсионной
кривой
в минимуме дисперсионной
кривой
![]() . Условие
. Условие
![]() получаем непосредственно из (6.1.5):
получаем непосредственно из (6.1.5):
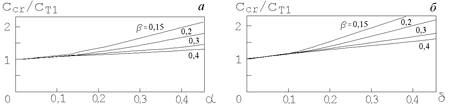 |
Рис. 6.2. Зависимость
необходимой для маргинальной
устойчивости диска как целого
дисперсии радиальных скоростей
в массивной подсистеме старых
звезд (
|
Совместное решение системы (6.1.6), (6.1.7) определяет
джинсовский масштаб
![]() (масштаб маргинально устойчивых
возмущений) и условие маргинальной устойчивости диска. В
частности, для однокомпонентного звездного диска (
(масштаб маргинально устойчивых
возмущений) и условие маргинальной устойчивости диска. В
частности, для однокомпонентного звездного диска (
![]() ) из
этой системы вытекает известный результат Тоомре [202]
) из
этой системы вытекает известный результат Тоомре [202]
В качестве первого примера рассмотрим модель, в которой диск-I
представляет собой массивную и "горячую" подсистему
старых звезд, диск-II -- маломассивную и "холодную"
подсистему молодых звезд (![]() ,
, ![]() ), а газовой подсистемы
нет (
), а газовой подсистемы
нет (![]() ). Результаты решения системы (6.1.6), (6.1.7) в рамках
этой модели представлены на рис. 6.1,а и 6.2,а. Из
рис. 6.1,а видно, что при
). Результаты решения системы (6.1.6), (6.1.7) в рамках
этой модели представлены на рис. 6.1,а и 6.2,а. Из
рис. 6.1,а видно, что при
![]() зависимость
зависимость
![]() однозначна, и с ростом
однозначна, и с ростом
![]() и уменьшением
и уменьшением
![]() граница устойчивости диска смещается в коротковолновую область,
но незначительно. При переходе к меньшим значениям
граница устойчивости диска смещается в коротковолновую область,
но незначительно. При переходе к меньшим значениям
![]() происходит качественное изменение -- зависимость
происходит качественное изменение -- зависимость
![]() становится неоднозначной: в некоторой области по параметру
становится неоднозначной: в некоторой области по параметру ![]() [
[
![]() ] уравнение (6.1.7)
имеет три вещественных корня. Два из них соответствуют двум минимумам на
дисперсионной кривой
] уравнение (6.1.7)
имеет три вещественных корня. Два из них соответствуют двум минимумам на
дисперсионной кривой
![]() , а третий -- максимуму
между ними (на рис. 6.1,а -- пунктиром). Длинноволновый минимум
обусловлен массивной подсистемой старых звезд, и он определяет маргинальную
устойчивость диска с
, а третий -- максимуму
между ними (на рис. 6.1,а -- пунктиром). Длинноволновый минимум
обусловлен массивной подсистемой старых звезд, и он определяет маргинальную
устойчивость диска с
![]() (см. рис. 6.1,а). Коротковолновый
же минимум создается "холодной" подсистемой молодых звезд. При
(см. рис. 6.1,а). Коротковолновый
же минимум создается "холодной" подсистемой молодых звезд. При
![]() дисперсионная кривая
дисперсионная кривая
![]() вновь имеет один минимум, лежащий уже в коротковолновой области и
обусловленный маломассивной "холодной" подсистемой звезд.
вновь имеет один минимум, лежащий уже в коротковолновой области и
обусловленный маломассивной "холодной" подсистемой звезд.
Рис. 6.1,а ярко демонстрирует интересную особенность составной
(двухкомпонентной) модели гравитирующего диска: если одна из
подсистем достаточно "холодна" (
![]() ), то даже будучи
весьма маломассивной (
), то даже будучи
весьма маломассивной (
![]() ) именно она
определяет величину джинсовского масштаба
) именно она
определяет величину джинсовского масштаба ![]() и
устойчивость диска в целом. В связи с
этим следует отметить, что если обе подсистемы будут в достаточной
мере "охлажденными", то в обоих минимумах дисперсионной кривой
может оказаться
и
устойчивость диска в целом. В связи с
этим следует отметить, что если обе подсистемы будут в достаточной
мере "охлажденными", то в обоих минимумах дисперсионной кривой
может оказаться
![]() . Таким обpазом могут возникать
две изолиpованные
. Таким обpазом могут возникать
две изолиpованные ![]() -области (два кольца на
-области (два кольца на ![]() -плоскости) неустойчивых
возмущений. Это означает, что в таком диске смогут возбуждаться
структуры с двумя сильно различающимися пространственными
масштабами (
-плоскости) неустойчивых
возмущений. Это означает, что в таком диске смогут возбуждаться
структуры с двумя сильно различающимися пространственными
масштабами (
![]() ). В общем же
случае
). В общем же
случае ![]() -компонентного диска при определенных ограничениях на
значения параметров подсистем могут возникнуть
-компонентного диска при определенных ограничениях на
значения параметров подсистем могут возникнуть ![]() изолированных
изолированных
![]() -областей гравитационно неустойчивых возмущений [355].
-областей гравитационно неустойчивых возмущений [355].
Значение величины
![]() , необходимой для маргинальной
устойчивости диска как целого при фиксированном
, необходимой для маргинальной
устойчивости диска как целого при фиксированном
![]() ,
является, очевидно, такой функцией параметра
,
является, очевидно, такой функцией параметра ![]() , что
, что
![]() . Эта функциональная
зависимость изображена на рис. 6.2,а. Видно, что в области
параметров
. Эта функциональная
зависимость изображена на рис. 6.2,а. Видно, что в области
параметров
![]() эта зависимость оказывается достаточно слабой:
эта зависимость оказывается достаточно слабой:
![]() , т.е. в соответствии с
результатом Тоомре [202] величина
, т.е. в соответствии с
результатом Тоомре [202] величина
![]() .
Однако если одна из подсистем достаточно "холодна" (
.
Однако если одна из подсистем достаточно "холодна" (
![]() ),
то в области
),
то в области
![]() величина
величина ![]() растет гораздо
быстрее с увеличением параметра
растет гораздо
быстрее с увеличением параметра ![]() . Тем не менее важно отметить,
что устойчивость диска с довольно массивной холодной подсистемой II
(
. Тем не менее важно отметить,
что устойчивость диска с довольно массивной холодной подсистемой II
(
![]() ) может быть обеспечена достаточно горячей подсистемой
старых звезд.
) может быть обеспечена достаточно горячей подсистемой
старых звезд.
Рассмотрим теперь другую составную модель -- двухкомпонентный
звездно-газовый диск, состоящий из подсистемы старых звезд
(
![]() ) и газовой подсистемы (
) и газовой подсистемы (
![]() ;
;
![]() ). На первый
взгляд может показаться, что результаты исследования такой модели
будут идентичны результатам, полученным для двухкомпонентного
звездного диска, с точностью до переобозначений
). На первый
взгляд может показаться, что результаты исследования такой модели
будут идентичны результатам, полученным для двухкомпонентного
звездного диска, с точностью до переобозначений
![]() ,
,
![]() . Однако это не так, поскольку динамика
возмущений в газовом диске описывается гидродинамическими уравнениями, а
в звездном -- бесстолкновительным кинетическим уравнением, и как раз в
области длин волн
. Однако это не так, поскольку динамика
возмущений в газовом диске описывается гидродинамическими уравнениями, а
в звездном -- бесстолкновительным кинетическим уравнением, и как раз в
области длин волн
![]() (или
(или
![]() )
эти способы описания не эквивалентны. Последнее обстоятельство оказывается
существенным, потому что даже для наиболее "холодных" подсистем молодых звезд
и газа
)
эти способы описания не эквивалентны. Последнее обстоятельство оказывается
существенным, потому что даже для наиболее "холодных" подсистем молодых звезд
и газа
![]() (здесь
(здесь
![]() ;
;
![]() -- длина волны спирального узора).
-- длина волны спирального узора).
Результаты вычислений в модели звездно-газового диска
изображены на рис. 6.1,б, 6.2,б. Качественно эти результаты не
отличаются от описанных выше для модели двухкомпонентного
звездного диска. Количественные же различия состоят в следующем.
Во-первых, появление коротковолнового минимума происходит при
большей относительной доле "холодной" (газовой) подсистемы:
![]() (ср.
рис. 6.1,а и
6.1,б). Во-вторых, величина необходимой для маргинальной
устойчивости диска
как целого
(ср.
рис. 6.1,а и
6.1,б). Во-вторых, величина необходимой для маргинальной
устойчивости диска
как целого
![]() с ростом параметра
с ростом параметра ![]() увеличивается существенно быстрее, чем с ростом параметра
увеличивается существенно быстрее, чем с ростом параметра
![]() в модели двухкомпонентного звездного диска
(ср. рис. 6.2,а и 6.2,б).
в модели двухкомпонентного звездного диска
(ср. рис. 6.2,а и 6.2,б).
Прежде чем перейти к конкретным оценкам в приложении к
Галактике, остановимся еще на трехкомпонентной модели диска
(старые звезды ![]() молодые звезды
молодые звезды ![]() газ) и роли конечной толщины
подсистем. Будем считать, что легкая подсистема молодых звезд (О,
В -- спектральных типов) обладает той же величиной дисперсии
радиальных скоростей, что и газ, т.е.
газ) и роли конечной толщины
подсистем. Будем считать, что легкая подсистема молодых звезд (О,
В -- спектральных типов) обладает той же величиной дисперсии
радиальных скоростей, что и газ, т.е.
![]() [53,70]. Тогда рассматриваемая модель характеризуется тремя
параметрами:
[53,70]. Тогда рассматриваемая модель характеризуется тремя
параметрами: ![]() ,
, ![]() ,
, ![]() . Результаты исследования этой
модели в наиболее интересном пределе
. Результаты исследования этой
модели в наиболее интересном пределе
![]() можно представить в
следующем виде. Зависимость обратного (нормированного) джинсовского
масштаба
можно представить в
следующем виде. Зависимость обратного (нормированного) джинсовского
масштаба ![]() от параметров модели практически соответствует
изображенной на рис. 6.1,б, если по горизонтальной оси откладывать не
от параметров модели практически соответствует
изображенной на рис. 6.1,б, если по горизонтальной оси откладывать не
![]() , а сумму
, а сумму
![]() . Величина
. Величина
![]() близка к изображенной на рис. 6.2,б,
но несколько меньше.
близка к изображенной на рис. 6.2,б,
но несколько меньше.
Однако наиболее существенное влияние на приведенные выше
результаты оказывает учет конечной толщины подсистем диска. Способ
учета этих величин известен (см. пп. 2.3.2, 4.2.2), и
соответствующие вычисления [487] показали, что при разумных
значениях
![]() и
и
![]() величина
величина
![]() (коротковолновый минимум становится глубже
длинноволнового, и именно он определяет границу гравитационной
устойчивости диска при
(коротковолновый минимум становится глубже
длинноволнового, и именно он определяет границу гравитационной
устойчивости диска при
![]() ). Близкие
результаты были также получены Джогом и Соломоном [488], исследовавшими
гравитационную неустойчивость двухкомпонентной модели диска, в которой и
звездная, и газовая подсистемы описывались в рамках
гидродинамического приближения.
). Близкие
результаты были также получены Джогом и Соломоном [488], исследовавшими
гравитационную неустойчивость двухкомпонентной модели диска, в которой и
звездная, и газовая подсистемы описывались в рамках
гидродинамического приближения.
На основании этих результатов сделаем предварительные оценки
для Галактики в окрестности Солнца (где и был сформулирован
"парадокс Тоомре":
![]() -- см. введение к настоящей
главе. По данным наиболее правдоподобной модели Галактики [24],
-- см. введение к настоящей
главе. По данным наиболее правдоподобной модели Галактики [24],
![]() М
М![]() /пк
/пк![]() ;
; ![]() кпк;
кпк;
![]() (км/с)/кпк и, следовательно, только по
старым звездам
(км/с)/кпк и, следовательно, только по
старым звездам
![]() кпк
(отличие от оценки Тоомре
кпк
(отличие от оценки Тоомре
![]() кпк связано в
основном с тем, что им использовалась модель Шмидта [291], в которой
кпк связано в
основном с тем, что им использовалась модель Шмидта [291], в которой
![]() М
М![]() /пк
/пк![]() ). Плотность газа [70]
). Плотность газа [70]
![]() М
М![]() /пк
/пк![]() . Отсюда
. Отсюда
![]() ,
а
,
а
![]() (здесь параметр
(здесь параметр ![]() учитывает только О,В -- звезды с
учитывает только О,В -- звезды с
![]() км/с). По старым звездам
км/с). По старым звездам
![]() км/с [53], а по газу
км/с [53], а по газу
![]() км/с [84].
Таким образом, нижняя оценка
км/с [84].
Таким образом, нижняя оценка
![]() ,
и согласно рис. 6.2,б
,
и согласно рис. 6.2,б
![]() , а из
рис. 6.1,б следует,
что наиболее близкий к границе устойчивости минимум дисперсионной
кривой
, а из
рис. 6.1,б следует,
что наиболее близкий к границе устойчивости минимум дисперсионной
кривой
![]() -- длинноволновый с
-- длинноволновый с
![]() . Отсюда получаем старый результат
. Отсюда получаем старый результат
![]() км/с и "парадокс Тоомре" в
окрестности Солнца не снимается. Аналогичные оценки не позволяют
надеяться на преодоление "парадокса Тоомре" и в области
км/с и "парадокс Тоомре" в
окрестности Солнца не снимается. Аналогичные оценки не позволяют
надеяться на преодоление "парадокса Тоомре" и в области ![]() .
Таким образом, для возбуждения спиральных волн плотности
коротковолновой гравитационной неустойчивостью в Галактике нет
необходимой доли "холодных" (газа и молодых звезд) подсистем.
Подобный вывод будет, по-видимому, справедлив и для большинства
других не слишком богатых газом галактик.
.
Таким образом, для возбуждения спиральных волн плотности
коротковолновой гравитационной неустойчивостью в Галактике нет
необходимой доли "холодных" (газа и молодых звезд) подсистем.
Подобный вывод будет, по-видимому, справедлив и для большинства
других не слишком богатых газом галактик.
6.1.2 Роль звездообразования
Для достаточно богатых газом плоских галактик рассмотренная
выше коротковолновая гравитационная неустойчивость может,
по-видимому, возбуждать структуры, характерные масштабы которых
порядка длины волны спирального узора. Неясным, однако, остается
механизм возбуждения неустойчивости, поскольку гравитационная
неустойчивость имеет тенденцию к достаточно быстрому
самоподавлению [189]. Обсудим с этой точки зрения возможность
возбуждения гравитационной неустойчивости процессом
звездообразования. Впервые на эту возможность указал Като
[489]. Им, в частности, было показано, что в модели двухкомпонентного
звездно-газового диска с
![]() и
и
![]() рождение звезд из газа приводит
к раскачке гравитационной неустойчивости, инкремент которой максимален для
возмущений джинсовского масштаба (
рождение звезд из газа приводит
к раскачке гравитационной неустойчивости, инкремент которой максимален для
возмущений джинсовского масштаба (
![]() ).
).
Исследуем этот вопрос в рамках рассмотренной выше
трехкомпонентной модели звездно-газового диска. Предположим, что в
начальный момент времени диск был маргинально устойчив, т.е.
![]() . Затем в течение промежутка времени
. Затем в течение промежутка времени ![]() часть газа превратилась в молодые звезды с
часть газа превратилась в молодые звезды с ![]() , т.е.
, т.е. ![]() и
и
![]() получили приращения, связанные соотношением
получили приращения, связанные соотношением
В системе с измененными ![]() и
и ![]() должна сместиться граница
устойчивости по длине волны на
должна сместиться граница
устойчивости по длине волны на ![]() от
от ![]() и
и ![]() измениться на
величину
измениться на
величину ![]() . Если при
. Если при ![]() окажется
окажется ![]() , то система
в целом станет неустойчивой, так как
, то система
в целом станет неустойчивой, так как
![]() . Таким образом,
обусловленная звездообразованием неустойчивость возникает, если
. Таким образом,
обусловленная звездообразованием неустойчивость возникает, если
Таким образом, процесс звездообразования приводит к раскачке гравитационной неустойчивости в первоначально устойчивом многокомпонентном галактическом диске. При этом, по-видимому, в диске галактики будут протекать релаксационные процессы, увеличивающие дисперсии скоростей объектов составляющих диск подсистем и, следовательно, стремящиеся возвратить систему к устойчивому состоянию. Однако продолжающиеся звездообразование и запаздывание релаксационных процессов будут поддерживать такую "тлеющую" неустойчивость вплоть до выхода диска на такое стационарное состояние, в котором процессы звездообразования и разрушения звезд окажутся взаимно скомпенсированными. Таким образом, процесс звездообразования оказывается постоянно действующим генератором структур джинсовского масштаба в многокомпонентном диске. Величина джинсовского масштаба зависит от доли "холодных" подсистем в диске и их "температуры".
6.1.3 Резонанс радиального потока газа с гравитационной спиральной волной
Интересным механизмом возбуждения гравитационных спиральных
волн плотности может быть механизм, обусловленный неустойчивостями
в системе с относительным движением ее подсистем. Неустойчивости
этого типа обычно называют пучковыми. Впервые, по-видимому, такой
механизм был изучен [490] в гидродинамических моделях
многокомпонентного диска с вращающимися с существенно различными
угловыми скоростями подсистемами. Позднее Като [491] рассмотрел
более реалистичную модель звездно-газового диска, в котором газ
помимо участия в общем вращении диска испытывает еще
макроскопическое движение в радиальном направлении. Дисперсионное
уравнение этой модели имеет вид [ср. с (6.1.4)]
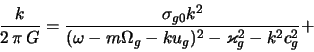
где
Дисперсионное уравнение (6.1.10) было решено Като [491] численно лишь при нескольких значениях входящих в него параметров, что не позволяет использовать полученные результаты для выяснения роли пучкового механизма в возбуждении спирального узора различных галактик. Приведем аналитическое исследование уравнения (6.1.10) и сделаем соответствующие оценки для Галактики [492].
Будем считать, что
![]() . Тогда
. Тогда
и тем самым можно положить
где
В соответствии с данными наблюдений полагаем
Так как
![]() и в устойчивом по Тоомре [202] диске
и в устойчивом по Тоомре [202] диске
![]() , искомая резонансная пучковая
неустойчивость (
, искомая резонансная пучковая
неустойчивость (
![]() ) имеет место при
) имеет место при
![]() (
(![]() ). Условие раскачки этой неустойчивости (условие резонанса) имеет вид
). Условие раскачки этой неустойчивости (условие резонанса) имеет вид
Для оценки необходимой для возбуждения наблюдаемой в
Галактике спиральной структуры величины радиальной скорости
газового потока ![]() используем приведенные в п. 6.1.1 данные
наблюдений и полагаем
используем приведенные в п. 6.1.1 данные
наблюдений и полагаем
![]() кпк [493]. Считая спираль
отстающей и двухрукавной (
кпк [493]. Считая спираль
отстающей и двухрукавной (![]() ,
, ![]() ), из (6.1.12) получаем
), из (6.1.12) получаем
![]() (знак
(знак ![]() выбран в соответствии с теорией Лина и
Шу [482]), а из (6.1.14) -- необходимую для возбуждения спиралей
выбран в соответствии с теорией Лина и
Шу [482]), а из (6.1.14) -- необходимую для возбуждения спиралей
![]() км/с. Полагая затем
км/с. Полагая затем
![]() (см. п. 6.1.1),
из (6.1.15) получаем
(см. п. 6.1.1),
из (6.1.15) получаем
![]() . Таким образом, даже при наличии
необходимой для раскачки исследуемой неустойчивости
. Таким образом, даже при наличии
необходимой для раскачки исследуемой неустойчивости
![]() характерное время возбуждения спирального узора, оцененное
по максимальному инкременту, равно
характерное время возбуждения спирального узора, оцененное
по максимальному инкременту, равно ![]() оборотов диска, что почти в
два раза превышает время сноса волнового спирального пакета к
центру Галактики [453].
оборотов диска, что почти в
два раза превышает время сноса волнового спирального пакета к
центру Галактики [453].
Радиальных потоков газа в окрестности Солнца с
![]() км/с, по-видимому, нет. Отсюда следует, что механизм резонансной
пучковой неустойчивости радиального потока газа в окрестности
км/с, по-видимому, нет. Отсюда следует, что механизм резонансной
пучковой неустойчивости радиального потока газа в окрестности ![]() не может быть генератором гравитационных спиральных волн
плотности. Отметим также, что в рамках теории Лина и Шу
согласно (6.1.14) резонансная пучковая неустойчивость может иметь
место только в случае направленного к центру Галактики радиального
потока газа.
не может быть генератором гравитационных спиральных волн
плотности. Отметим также, что в рамках теории Лина и Шу
согласно (6.1.14) резонансная пучковая неустойчивость может иметь
место только в случае направленного к центру Галактики радиального
потока газа.
Нетрудно видеть, что минимально необходимая для раскачки
резонансной пучковой неустойчивостью гравитационных спиральных
волн плотности величина
![]() может быть достигнута на коротационном радиусе, где
может быть достигнута на коротационном радиусе, где ![]() .
Абсолютный минимум
.
Абсолютный минимум
![]() достигается,
если в этой области
достигается,
если в этой области
![]() .
Такая оценка показывает, что пучковый механизм
вряд ли перспективен как механизм возбуждения спирального узора в
плоских галактиках.
.
Такая оценка показывает, что пучковый механизм
вряд ли перспективен как механизм возбуждения спирального узора в
плоских галактиках.
6.1.4 Нелинейное насыщение резонансного усиления спиральных волн на коротационном радиусе
Благодаря дифференциальности вращения диска спиральной
галактики
![]() на некотором расстоянии от ее центра
на некотором расстоянии от ее центра
![]() угловая скорость спирального узора равна
угловая скорость спирального узора равна
![]() (величину
(величину ![]() называют коротационным радиусом).
Поэтому звезды диска,
локализованные в окрестности коротационного радиуса, оказываются в
резонансе со спиральной волной. Линден-Белл и Калнайс [494]
показали, что в рамках линейной теории такое резонансное
взаимодействие волны со звездами диска приводит к усилению волны
(физика этого процесса подробно описана Фридманом и Поляченко [2]).
называют коротационным радиусом).
Поэтому звезды диска,
локализованные в окрестности коротационного радиуса, оказываются в
резонансе со спиральной волной. Линден-Белл и Калнайс [494]
показали, что в рамках линейной теории такое резонансное
взаимодействие волны со звездами диска приводит к усилению волны
(физика этого процесса подробно описана Фридманом и Поляченко [2]).
Усиливающаяся таким образом волна должна оказывать влияние на динамику резонансных звезд, меняя их функцию распределения и тем самым условия усиления волны. Поэтому ясно, что исследование эффективности механизма резонансного усиления спиральных гравитационных волн на коротационном радиусе в нелинейном режиме является весьма актуальным. Проведем изучение этого вопроса, следуя работе [495].
В системе отсчета, вращающейся с угловой скоростью
спирального узора ![]() , величину энергии отдельной звезды можно
представить в виде
, величину энергии отдельной звезды можно
представить в виде
где
Уравнения движения отдельной звезды вытекают из уравнений
Гамильтона:
![]() ;
;
![]() . Ограничиваясь малой окрестностью коротационного радиуса
. Ограничиваясь малой окрестностью коротационного радиуса
Из (6.1.20), (6.1.22) видно, что условие резонанса звезды в плоскости (
Из уравнений (6.1.21), (6.1.22) следует, что ![]() . Это
обстоятельство позволяет упростить задачу, перейдя от системы
(6.1.19)-(6.1.22), описывающей движение отдельной звезды, к
уравнениям, описывающим движение центра ее эпицикла. Такой переход
может быть выполнен с помощью метода усреднения по "быстрой" фазе
. Это
обстоятельство позволяет упростить задачу, перейдя от системы
(6.1.19)-(6.1.22), описывающей движение отдельной звезды, к
уравнениям, описывающим движение центра ее эпицикла. Такой переход
может быть выполнен с помощью метода усреднения по "быстрой" фазе
![]() , разработанного Боголюбовым и Митропольским
[496]6.2. Для этого
представим переменные "действие-угол" в виде
, разработанного Боголюбовым и Митропольским
[496]6.2. Для этого
представим переменные "действие-угол" в виде
![]() ;
;
![]() , где
, где
![]() ,
,
![]() описывают "дрожательное" движение с
быстрой фазой
описывают "дрожательное" движение с
быстрой фазой ![]() , а
, а ![]() ,
, ![]() -- плавное движение с
медленной фазой
-- плавное движение с
медленной фазой ![]() . Оставляя в дальнейших вычислениях для плавно меняющихся
величин прежние обозначения (без знака усреднения), из системы
(6.1.19)-(6.1.22) получим
. Оставляя в дальнейших вычислениях для плавно меняющихся
величин прежние обозначения (без знака усреднения), из системы
(6.1.19)-(6.1.22) получим
и, кроме того,
Представим гравитационный потенциал спиральной волны во
вращающейся с угловой скоростью ![]() системе отсчета в виде
системе отсчета в виде
где величина
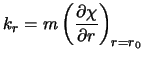 ;
;
Полагая затем без ограничения общности
![]() и
обозначая фазу спиральной волны
и
обозначая фазу спиральной волны
![]() , приведем систему
(6.1.23), (6.1.24) к уравнению
, приведем систему
(6.1.23), (6.1.24) к уравнению
где в соответствии с наблюдениями считалось ![]() , a связь
координат центра эпицикла
, a связь
координат центра эпицикла ![]() ,
, ![]() с фазой
с фазой ![]() определяется
соотношениями
определяется
соотношениями
Уравнение (6.1.28), к решению которого свелась задача о
движении центра эпицикла звезды в поле спиральной волны, имеет
интеграл энергии
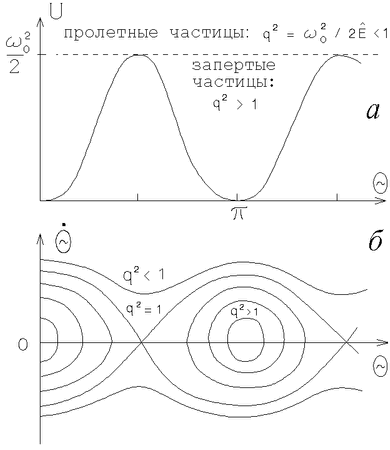 |
Рис. 6.3. а -- эффективный
потенциал
|
Решение (6.1.28) может быть получено как в эллиптических
функциях, так и в более наглядном виде -- асимптотическом. Однако
даже не решая это уравнение, можно получить качественное
представление о характере движения центров эпициклов (в дальнейшем
для краткости -- частиц). Эффективный потенциал [см. (6.1.30)], в
котором движутся такие частицы, изображен на рис. 6.3,а. Видно, что
все частицы можно разделить на запертые в волне, для которых
![]() , и пролетные, для которых
, и пролетные, для которых ![]() .
Траектории этих частиц на фазовой плоскости (
.
Траектории этих частиц на фазовой плоскости (
![]() ) изображены
на рис. 6.3,б.
) изображены
на рис. 6.3,б.
Запертые частицы благодаря тому, что эффективный потенциал
(см. рис. 6.3,а) не является квадратичным, в зависимости от
величины параметра ![]() обладают различными периодами движения по
координате
обладают различными периодами движения по
координате ![]() . Таким образом, в окрестности коротационного радиуса
возникает перемешивание частиц в фазовом пространстве, в
результате чего на функции распределения этих частиц должно
возникать плато за промежуток времени порядка
. Таким образом, в окрестности коротационного радиуса
возникает перемешивание частиц в фазовом пространстве, в
результате чего на функции распределения этих частиц должно
возникать плато за промежуток времени порядка
![]() (известны аналогичные нелинейные эффекты в плазме,
физика этого
процесса прекрасно описана Кадомцевым [497]).
(известны аналогичные нелинейные эффекты в плазме,
физика этого
процесса прекрасно описана Кадомцевым [497]).
Если охарактеризовать интенсивность волны безразмерной
амплитудой гравитационной силы
![]() , то характерное
время
, то характерное
время
![]() , где
, где
![]() (по параметрам спиральных волн в
Галактике
(по параметрам спиральных волн в
Галактике
![]() ). После возникновения плато рост амплитуды
волны, обусловленный градиентом функции распределения в фазовом
пространстве, должен прекратиться. Поэтому для проверки
эффективности предложенного Линден-Беллом и Калнайсом [494]
механизма усиления спиральных волн необходимо вычислить амплитуду
насыщения волны к моменту "выключения" этого механизма и уточнить
величину промежутка времени его работы.
). После возникновения плато рост амплитуды
волны, обусловленный градиентом функции распределения в фазовом
пространстве, должен прекратиться. Поэтому для проверки
эффективности предложенного Линден-Беллом и Калнайсом [494]
механизма усиления спиральных волн необходимо вычислить амплитуду
насыщения волны к моменту "выключения" этого механизма и уточнить
величину промежутка времени его работы.
Спиральная волна, будучи волной отрицательной энергии в
области ![]() , должна резонансным образом усиливаться в
окрестности коротационного радиуса за счет передачи момента
, должна резонансным образом усиливаться в
окрестности коротационного радиуса за счет передачи момента ![]() и
энергии
и
энергии ![]() резонансным звездам. Темп такой передачи в рамках
линейной теории определяется следующими соотношениями:
резонансным звездам. Темп такой передачи в рамках
линейной теории определяется следующими соотношениями:
где
а
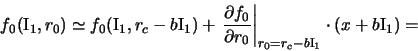
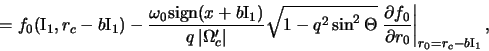
где в
а функция распределения пролетных частиц примет вид
где
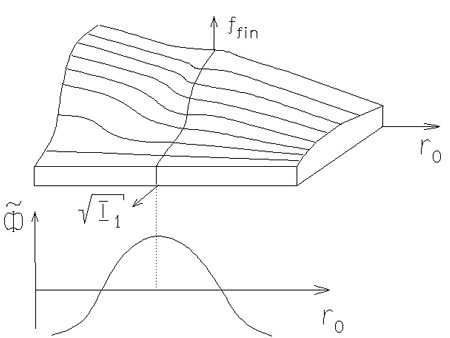 |
Рис. 6.4. Конечная
функция распределения
звезд в направлении |
Наглядное представление о функции распределения (6.1.36),
(6.1.37) можно получить из рис. 6.4. В качестве начальной функции
распределения
![]() при построении этого рисунка была взята
шварцшильдовская (2.1.44) с
при построении этого рисунка была взята
шварцшильдовская (2.1.44) с
![]() ;
;
![]() ;
;
![]() ;
; ![]() и параметрами волны
и параметрами волны
![]() ;
;
![]() [498]. Рис. 6.4 представляет
[498]. Рис. 6.4 представляет ![]() в
направлении
в
направлении ![]() в спиральном гравитационном потенциале
(6.1.26) с
в спиральном гравитационном потенциале
(6.1.26) с
![]() .
.
Величину переданного волне момента от резонансных частиц
где величины
характеризуют вклады в передачу момента и энергии спиральной волне от запертых и пролетных частиц соответственно [
Из сравнения (6.1.32) с (6.1.39) следует
Предположим теперь, что в Галактике возникли спиральные волны
бесконечно малой амплитуды, и оценим амплитуду их насыщения
благодаря работе механизма резонансного усиления таких волн на
коротационном радиусе. Для этого необходимо приравнять момент,
который может быть передан волне резонансными звездами (6.1.39),
моменту волны [194]
Тогда по порядку величины
Полагая в (6.1.39) функцию распределения звезд шварцшильдовской, получаем оценку амплитуды насыщения волны
где
Для обычно принимаемого в Галактике значения
![]() [498,500] это дает
[498,500] это дает
![]() , что по крайней
мере на порядок
меньше значений, получающихся в результате сравнения расчетных и
наблюдаемых кинематических эффектов, связанных с динамикой
спиральных волн в Галактике.
, что по крайней
мере на порядок
меньше значений, получающихся в результате сравнения расчетных и
наблюдаемых кинематических эффектов, связанных с динамикой
спиральных волн в Галактике.
Решенная здесь задача близка по смыслу к задаче о нелинейном
взаимодействии системы заряженных частиц с волной электрического
потенциала [497]. В то же время в отличие от плазмы, где в
резонансе с волной оказывается малая доля частиц в пространстве
скоростей, в нашем случае волна находится в резонансе почти со
всеми частицами скоростного пространства, локализованными, однако,
в малой окрестности коротационного радиуса. Этот фактор "портит"
пространственное распределение гравитационного потенциала, и для
того, чтобы его влиянием можно было пренебречь, ширина
образующегося плато ![]() должна быть мала по сравнению с длиной
волны
должна быть мала по сравнению с длиной
волны
![]() . Из (6.1.29)-(6.1.31) следует оценка
. Из (6.1.29)-(6.1.31) следует оценка
![]() , и поэтому
, и поэтому
![]() по параметрам
спиральной структуры Галактики.
по параметрам
спиральной структуры Галактики.
Необходимо также отметить, что, согласно Галееву и Сагдееву [501],
результаты задачи о нарастании волны до конечной амплитуды в
отличие от результатов задачи о затухании волны конечной амплитуды
следует рассматривать лишь как оценку, поскольку при вычислении
движения частиц ростом потенциала пренебрегали. Тем не менее
полученный здесь вывод о неэффективности резонансного усиления
спиральной волны на коротационном радиусе верен, так как оценка
амплитуды насыщения волны (6.1.46) показывает, что
![]() .
.
Заметим еще, что в похожей на плазменную постановке в [502] была решена задача о нелинейном взаимодействии пучка звезд, движущегося вдоль оси самогравитирующего цилиндра с волной, распространяющейся в том же направлении.
<< 6. Природа спирального узора | Оглавление | 6.2 Гидродинамическая концепция ... >>