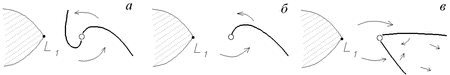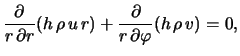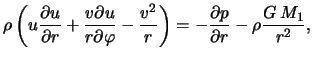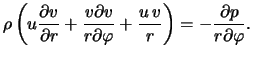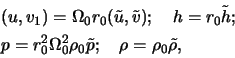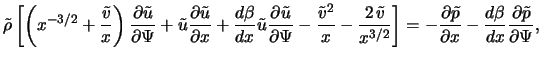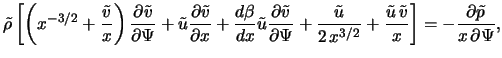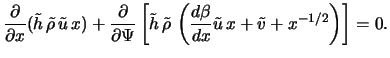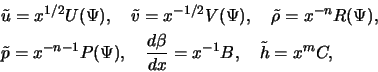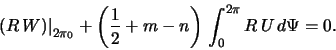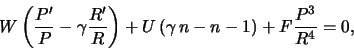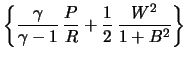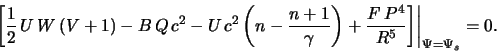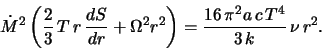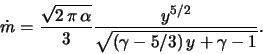|
Астронет: А. Г. Морозов, А. В. Хоперсков Физика Дисков http://www.astronet.ru/db/msg/1168623/node32.html |
<< 5.1 Осесимметричная дисковая аккреция | Оглавление | 5.3 Неустойчивости аккреционных ... >>
- 5.2.1 Газодинамическое моделирование перетекания вещества в ТДС. Условия образования диска
- 5.2.2 Автомодельные ударные волны
- 5.2.3 Спиральные ударные волны в ТДС. Газодинамическое моделирование
5.2 Неосесимметричная дисковая аккреция
5.2.1 Газодинамическое моделирование перетекания вещества в ТДС. Условия образования диска
Как мы увидели в разд. 5.1, в рамках осесимметричных моделей удается понять многие наблюдаемые проявления АД. В то же время в тесных двойных системах аккреционные диски являются принципиально неосесимметричными в силу гравитационного влияния со стороны нормальной звезды и того, что вещество попадает в АД в форме струи через внутреннюю лагранжеву точку. Если изучаются достаточно длительные промежутки времени, существенно превышающие период обращения, то, казалось бы, стандартные модели АД являются хорошим приближением. Поскольку вещество при своем движении к аккрецирующему объекту делает много оборотов, то за это время происходит перемешивание вещества по углу. Гравитационная сила нормальной компоненты при приближении к компактному объекту становится сколь угодно малой по сравнению с силой, обусловленной центральной массой.
Возникает ряд интересных вопросов: при каких условиях в ТДС возникает АД? Какая часть вещества теряется системой? Будет ли вещество аккрецировать без вязкости? Задачи такого рода являются для любителей аналитических решений практически неразрешимыми в силу нестационарности и неодномерности. И почти единственный выход -- численное моделирование.
Вещество может покидать оптическую звезду в форме звездного ветра, т.е. со всей поверхности звезды. Другой режим может возникать при заполнении нормальной звездой своей критической области Роша, когда вещество истекает в форме струи через достаточно малую окрестность внутренней точки Лагранжа. При этом если скорость газа достаточно велика, то трудно ожидать образования диска.
Из самых общих соображений ясно, что при аккреции в ТДС возможно возникновение ударных волн. Бирман [436], по-видимому, был первым, кто в рамках гидродинамического подхода рассмотрел течение газа в близкой двойной системе в режиме звездного ветра. Методом характеристик было рассмотрено только сверхзвуковое течение. Заведомо такое решение не может содержать ударных волн. В работе [437] получена коническая ударная волна за аккрецирующим объектом. Однако используемый метод конечных разностей, имеющий первый порядок точности, приводит к слишком большой численной вязкости. Кроме того, декартова сетка не позволяет правильно задать граничные условия на поверхности обеих звезд.
В работах [438-444] применялись численные схемы
второго порядка на криволинейной сетке, координатные линии которой
близки к изолиниям эффективного потенциала системы, состоящей из
двух тел (
![]() ), находящихся на расстоянии
), находящихся на расстоянии ![]() друг от друга
и вращающихся с угловой скоростью
друг от друга
и вращающихся с угловой скоростью ![]() . Одна из звезд заполняет свою
критическую область Роша, а радиус другой не превышает
. Одна из звезд заполняет свою
критическую область Роша, а радиус другой не превышает ![]() .
Эффекты, связанные с охлаждением, нагревом,
вязкостью5.7 и
магнитными полями, не принимались во внимание. На поверхности
нормальной звезды задавались значения плотности
.
Эффекты, связанные с охлаждением, нагревом,
вязкостью5.7 и
магнитными полями, не принимались во внимание. На поверхности
нормальной звезды задавались значения плотности ![]() и скорости
звука
и скорости
звука ![]() .
.
Исследованию течений при различных
![]() посвящены работы
[439,442] для
посвящены работы
[439,442] для ![]() . Если скорость звука мала (
. Если скорость звука мала (
![]() ),
то вокруг компактного объекта возникает диск с двумя спиральными ударными
волнами5.8(рис. 5.5, а). Максимальное число Маха
),
то вокруг компактного объекта возникает диск с двумя спиральными ударными
волнами5.8(рис. 5.5, а). Максимальное число Маха
![]() не
превышает
не
превышает ![]() . В случае
. В случае
![]() происходит
перестройка течения:
диск становится менее выраженным, при этом остается только одна
спиральная ударная волна (рис. 5.5, б). При значениях
происходит
перестройка течения:
диск становится менее выраженным, при этом остается только одна
спиральная ударная волна (рис. 5.5, б). При значениях ![]() , лежащих в
области
, лежащих в
области
![]() , возникает коническая ударная волна
(рис. 5.5, в), внутри конуса течение становится существенно
дозвуковым. При дальнейшем увеличении скорости звука
(
, возникает коническая ударная волна
(рис. 5.5, в), внутри конуса течение становится существенно
дозвуковым. При дальнейшем увеличении скорости звука
(
![]() )
образуется ярко выраженный режим звездного ветра. С ростом
скорости звука на поверхности звезды-донора угол между ударными
волнами становится меньше. Проходя через коническую ударную волну,
скорость газа сильно уменьшается и часть его аккрецирует на
компактный объект. Большая часть вещества из системы уходит.
Похожие результаты получены в работе [445].
)
образуется ярко выраженный режим звездного ветра. С ростом
скорости звука на поверхности звезды-донора угол между ударными
волнами становится меньше. Проходя через коническую ударную волну,
скорость газа сильно уменьшается и часть его аккрецирует на
компактный объект. Большая часть вещества из системы уходит.
Похожие результаты получены в работе [445].
Таким образом, тип аккрецирующего течения (истечение с
образованием диска или в форме звездного ветра с возникновением
конической ударной волны) в системе с заполнившей свою полость
Роша звездой-донором определяется значением параметра
![]() . Типичной для рассматриваемых систем является оценка
. Типичной для рассматриваемых систем является оценка
![]() см/с, что соответствует температуре
см/с, что соответствует температуре ![]() К.
В отсутствие звездной короны температура истекающего из звезды вещества
много меньше
К.
В отсутствие звездной короны температура истекающего из звезды вещества
много меньше ![]() K. Следовательно, наиболее вероятен режим истечения
через внутреннюю точку Лагранжа с образованием аккреционного диска
вокруг компактного объекта. При перетекании вещества через
внутреннюю точку Лагранжа велик удельный угловой момент вещества,
что приводит к образованию диска. В случае звездного ветра
удельный угловой момент достаточно мал и диск не образуется [144].
K. Следовательно, наиболее вероятен режим истечения
через внутреннюю точку Лагранжа с образованием аккреционного диска
вокруг компактного объекта. При перетекании вещества через
внутреннюю точку Лагранжа велик удельный угловой момент вещества,
что приводит к образованию диска. В случае звездного ветра
удельный угловой момент достаточно мал и диск не образуется [144].
5.2.2 Автомодельные ударные волны
Предположение о том, что в газовых дисках, вращающихся вокруг
компактных объектов, могут возникать спиральные ударные волны,
высказывалось неоднократно [446,447]. Притягательность их изучения
связана с тем, что спиральные ударные волны могут переносить
угловой момент из внутренних областей диска во внешние. В тонких
аккреционных дисках (![]() ) течение является сверхзвуковым, что
допускает возможность возникновения ударных волн. Причинами
возникновения ударных волн могут являться вторая компонента в
системе либо асимметричная магнитосфера вокруг компактного
объекта [448]. Благодаря диссипативным процессам на фронте волны
вещество может по спирали падать на центр.
) течение является сверхзвуковым, что
допускает возможность возникновения ударных волн. Причинами
возникновения ударных волн могут являться вторая компонента в
системе либо асимметричная магнитосфера вокруг компактного
объекта [448]. Благодаря диссипативным процессам на фронте волны
вещество может по спирали падать на центр.
Рассмотрим стационарное течение, содержащее две и более
спиралевидные ударные волны, в рамках автомодельного подхода [449].
Запишем стационарные уравнения газодинамики в следующей форме:
Будем полагать, что полутолщина
Первый случай соответствует строго двумерному течению в плоскости диска. Во-втором принимается, что газ находится в гидростатическом равновесии в
где
В случае термодинамического равновесия для большой оптической толщины
Считаем, что непрозрачность
Пользуемся безразмерными величинами, которые пометим сверху значком ``
где
функция
С учетом (5.2.9)-(5.2.12) уравнения (5.2.1)-(5.2.3) примут вид
Решения ищем в автомодельном виде
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() -- постоянные. Если
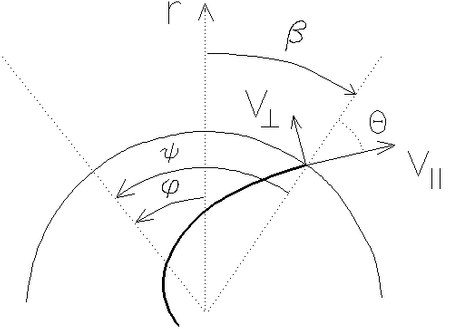
-- постоянные. Если ![]() есть угол между касательной к спирали (
есть угол между касательной к спирали (![]() const) и радиальным
направлением (рис. 5.6), то
const) и радиальным
направлением (рис. 5.6), то
Как видим, параметр
здесь
Первое слагаемое в (5.2.23) равно нулю. Второй член определяет темп аккреции, который отличен от нуля в случае наличия ударных волн. Следовательно,
Итак, в случае
Для сохранения автомодельности уравнения (5.2.6) с учетом (5.2.7), (5.2.8), (5.2.13) необходимо положить
где
Здесь
Систему уравнений (5.2.20 ![]() 5.2.22), (5.2.26) относительно
неизвестных
5.2.22), (5.2.26) относительно
неизвестных ![]() ,
, ![]() ,
, ![]() ,
, ![]() необходимо дополнить граничными условиями.
Рассмотрим
необходимо дополнить граничными условиями.
Рассмотрим ![]() одинаковых ударных волн, разделенных фиксированным
углом
одинаковых ударных волн, разделенных фиксированным
углом ![]() , тогда решения должны быть периодичны с периодом
, тогда решения должны быть периодичны с периодом
![]() . Запишем выражения для нормальной и касательной
к линии
. Запишем выражения для нормальной и касательной
к линии ![]() компонент скорости (рис. 5.6)
компонент скорости (рис. 5.6)
Таким образом, нормальная компонента потока вещества пропорциональна величине
Здесь через
где
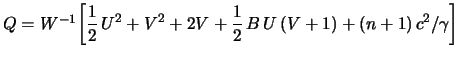 ,
,
Условия (5.2.31)-(5.2.33), (5.2.35) определяют постоянные интегрирования уравнений (5.2.20), (5.2.21), (5.2.25), (5.2.26).
В предельном случае большого числа ударных волн можно решить
задачу аналитически [449]. Рассмотрим только адиабатическое
течение [![]() в (5.2.26)]. Если исходить из малости параметра
в (5.2.26)]. Если исходить из малости параметра
![]() и предположения о том, что функции
и предположения о том, что функции ![]() являются линейными между ударными волнами, то можно записать соотношение
между
являются линейными между ударными волнами, то можно записать соотношение
между ![]() и углом спирали
и углом спирали ![]() [449]:
[449]:
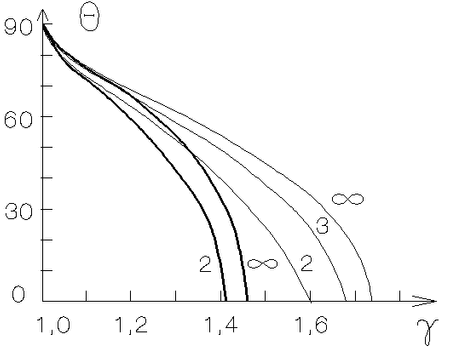 |
Рис. 5.7. Зависимость угла |
Численный подход к решению сформулированной выше задачи
позволяет рассматривать произвольное число ударных волн, в том
числе с учетом радиационных потерь. Результаты такого рода
расчетов приведены на рис. 5.7. Включение радиационных потерь
позволяет оценить эффективный ![]() -параметр, фигурирующий в "вязких
осесимметричных моделях" (см. разд. 5.1). Если определить средний
радиальный поток
-параметр, фигурирующий в "вязких
осесимметричных моделях" (см. разд. 5.1). Если определить средний
радиальный поток
то, сравнивая с результатом, вытекающим из стандартной модели АД
получим
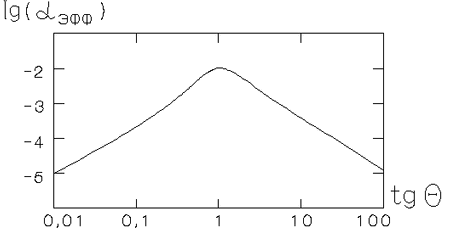
На рис. 5.8 показан коэффициент
![]() как функция угла
как функция угла ![]() .
В случае двух ударных волн (
.
В случае двух ударных волн (![]() ) имеется максимум при
) имеется максимум при
![]() и
и
![]() .
.
5.2.3 Спиральные ударные волны в ТДС. Газодинамическое моделирование
В п. 5.2.1 уже упоминались некоторые результаты численного газодинамического моделирования перетекания вещества в тесной двойной системе. Обсудим здесь подробнее проблему спиральных ударных волн в газовом диске, инициированных гравитационным потенциалом спутника -- нормальной звездой.
Прежде всего, в работах [438,439] было показано, что:
- газ теряется нормальной звездой через окрестность точки
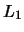 в
форме сверхзвуковой струи (см. рис. 1.2);
в
форме сверхзвуковой струи (см. рис. 1.2);
- основная часть вещества вращается вокруг компактного объекта в
форме аккреционного кольца/диска;
- в результате приливного взаимодействия образуется две или три
спиралевидные ударные волны (УВ);
- газ нагревается в УВ, теряет свой угловой момент относительно
аккрецирующей звезды. Количество углового момента, теряемого в УВ,
больше, чем из-за численной (схемной) вязкости;
- система может терять значительную часть вещества через точку
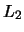 ;
;
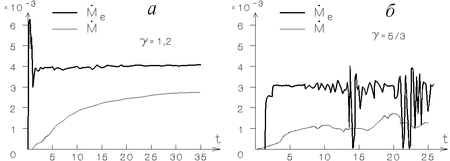
- величина темпа потери вещества оптической звездой
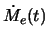 может
достаточно сильно осциллировать, в то время как темп аккреции
может
достаточно сильно осциллировать, в то время как темп аккреции
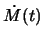 является более гладкой функцией (рис. 5.9);
является более гладкой функцией (рис. 5.9);
- отношение
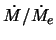 сильно зависит от параметров системы и
составляет
сильно зависит от параметров системы и
составляет 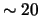 -90%.
-90%.
Причиной возникновения ударных волн является вторая
компонента, т.е. генератор находится на периферии АД, тем самым
возникает вопрос о том, как близко к аккрецирующему объекту могут
простираться УВ. Для решения этой проблемы была проведена серия
экспериментов [440], в которых размер компактного объекта равнялся
![]() . Поскольку для тесных двойных с периодом от нескольких
часов до дней величина
. Поскольку для тесных двойных с периодом от нескольких
часов до дней величина ![]() составляет
составляет
![]() см, то
см, то
![]() см, что соответствует радиусу белого карлика.
Если компактным объектом является нейтронная звезда с магнитным полем
см, что соответствует радиусу белого карлика.
Если компактным объектом является нейтронная звезда с магнитным полем ![]() Гс, то диск разрушается на расстоянии
Гс, то диск разрушается на расстоянии
![]() см
[451]. Расчеты убедительно продемонстрировали, что ударные волны
простираются вплоть до
см
[451]. Расчеты убедительно продемонстрировали, что ударные волны
простираются вплоть до ![]() .
.
Обсудим влияние численной вязкости. Используемые численные
схемы для решения уравнений газодинамики имеют II порядок точности
и дают схемное число Рейнольдса
![]() (
(![]() -- размер ячейки). Вблизи компактного объекта
-- размер ячейки). Вблизи компактного объекта ![]() . Таким
образом, угловой момент отводится наружу и газ падает на центр
даже в случае осесимметричного потенциала (без ударных волн). Эффект
численной вязкости можно снизить, уменьшая величину
. Таким
образом, угловой момент отводится наружу и газ падает на центр
даже в случае осесимметричного потенциала (без ударных волн). Эффект
численной вязкости можно снизить, уменьшая величину ![]() .
Для ответа на вопрос: какая часть углового момента теряется в УВ, был
поставлен эксперимент [438], в котором в момент времени
.
Для ответа на вопрос: какая часть углового момента теряется в УВ, был
поставлен эксперимент [438], в котором в момент времени
![]() (диск находится в состоянии квазистационара) каждая пространственная
ячейка в радиальном направлении делилась пополам и расчет
продолжался до
(диск находится в состоянии квазистационара) каждая пространственная
ячейка в радиальном направлении делилась пополам и расчет
продолжался до
![]() . В целом глобальная структура течения не
изменялась, а усредненная величина
. В целом глобальная структура течения не
изменялась, а усредненная величина
![]() уменьшалась от
уменьшалась от
![]() до
до ![]() . Таким образом, по оценкам авторов около 60
. Таким образом, по оценкам авторов около 60![]() 70 % общих потерь углового момента связаны с ударными волнами.
70 % общих потерь углового момента связаны с ударными волнами.
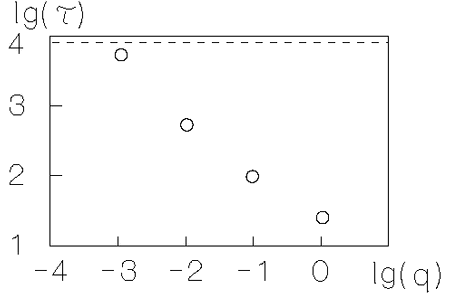
Процесс аккреции удобно характеризовать временем аккреции
![]() (
(![]() -- масса диска). На рис. 5.10 показана
экспериментальная зависимость величины
-- масса диска). На рис. 5.10 показана
экспериментальная зависимость величины ![]() от отношения масс компонент
от отношения масс компонент
![]() [443]. Горизонтальная линия соответствует осесимметричной
модели (
[443]. Горизонтальная линия соответствует осесимметричной
модели (![]() ), в которой аккреция полностью обусловлена численной
вязкостью. В рамках вязкой стандартной модели АД величина
), в которой аккреция полностью обусловлена численной
вязкостью. В рамках вязкой стандартной модели АД величина
![]() (п. 5.1.1). Для вязкости
(п. 5.1.1). Для вязкости
![]() имеем
имеем
В перечисленных выше работах в расчеты не включались радиационные потери, что приводило к высокой температуре, близкой к вириальной. Учет процессов охлаждения должен, с одной стороны, увеличить характерное число Маха. С другой стороны, в рамках автомодельного подхода (п. 5.2.2) с уменьшением температуры уменьшается амплитуда ударных волн. Выяснение роли этих факторов еще требует анализа.
Обсудим результаты, вытекающие из описанного выше
газодинамического моделирования, в сравнении с автомодельными
решениями (п. 5.2.2). Из рис. 5.7 видно, что стационарные
автомодельные решения, содержащие две спиральные УВ в диске
постоянной толщины, невозможны для
![]() . Численное
моделирование при
. Численное
моделирование при ![]() приводит к сильно осциллирующим течениям
(см. рис. 5.9), т.е. стационарные решения также не получаются. При
приводит к сильно осциллирующим течениям
(см. рис. 5.9), т.е. стационарные решения также не получаются. При
![]() осцилляции малы (рис. 5.9), и непосредственное
сопоставление угла спирали
осцилляции малы (рис. 5.9), и непосредственное
сопоставление угла спирали ![]() автомодельной волны с
экспериментальными результатами дает удовлетворительное согласие.
Сравнению результатов численного моделирования ударных волн,
автомодельных решений и стандартной теории дисковой аккреции
посвящена работа [444]. Зависимость угла закрутки УВ
автомодельной волны с
экспериментальными результатами дает удовлетворительное согласие.
Сравнению результатов численного моделирования ударных волн,
автомодельных решений и стандартной теории дисковой аккреции
посвящена работа [444]. Зависимость угла закрутки УВ ![]() от
показателя адиабаты5.9 показана на
рис. 5.11. Измерения
от
показателя адиабаты5.9 показана на
рис. 5.11. Измерения ![]() относятся к внутренней зоне АД, где влияние
второй компоненты минимально. В области
относятся к внутренней зоне АД, где влияние
второй компоненты минимально. В области
![]() имеется
хорошее согласие. В численных экспериментах при
имеется
хорошее согласие. В численных экспериментах при
![]() две стационарные ударные волны не появлялись, автомодельный
подход также запрещает их существование при
две стационарные ударные волны не появлялись, автомодельный
подход также запрещает их существование при
![]() (см.
рис. 5.7, 5.11). В области
(см.
рис. 5.7, 5.11). В области
![]() возможны стационарные
решения с числом УВ больше двух. На рис. 5.12 показаны радиальные зависимости
числа Маха ударной волны
возможны стационарные
решения с числом УВ больше двух. На рис. 5.12 показаны радиальные зависимости
числа Маха ударной волны ![]() . Наблюдается существенное различие по
сравнению с автомодельными решениями во внешней области АД, которое
уменьшается при приближении к центру. Такое поведение, по-видимому, вызвано
тем, что приливное взаимодействие при построении автомодельных решений
не учитывалось.
. Наблюдается существенное различие по
сравнению с автомодельными решениями во внешней области АД, которое
уменьшается при приближении к центру. Такое поведение, по-видимому, вызвано
тем, что приливное взаимодействие при построении автомодельных решений
не учитывалось.
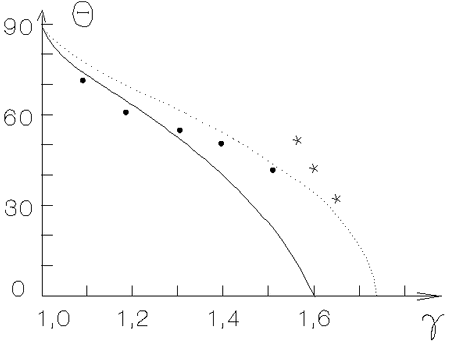 |
Рис. 5.11. Зависимости угла |
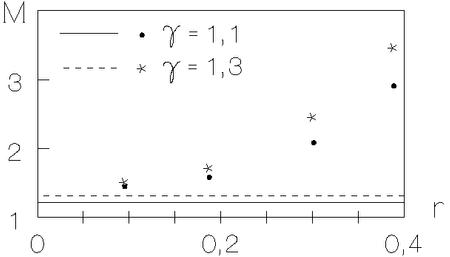 |
Рис. 5.12. Зависимость числа Маха ударной волны от радиальной координаты. Линиями показаны автомодельные решения. |
Удивительным, на первый взгляд, аспектом вышеописанных
результатов является возможность аккреции без радиационных потерь.
В противоположность этому в рамках стандартной дисковой аккреции
вся диссипирующая энергия высвечивается. В связи с этим рассмотрим
автомодельные волны с радиацией (п. 5.2.2). Зависимость температуры
от темпа аккреции в случае гидростатического равновесия в
![]() -направлении показана на рис. 5.13. Здесь безразмерный темп
аккреции
-направлении показана на рис. 5.13. Здесь безразмерный темп
аккреции ![]() определен следующим образом
определен следующим образом
 |
Рис. 5.13. Зависимость
безразмерной температуры
|
Уравнение (5.1.17), выражающее баланс энергии, запишем для
стационарного случая в виде
Если предположить
где
Зависимости
Из (5.2.47) следует, что адиабатическая аккреция возможна только для
Совершенно очевидно, что обсуждаемые здесь ударные волны весьма сходны с рассматриваемыми в теории спиральной структуры галактик. Рассмотрим (возможно слабый) источник неосесимметричных возмущений во внешней области диска. Им может являться не только вторая компонента, но и, например, какая-либо неустойчивость. Такое возмущение распространяется по диску, принимая спиральную форму благодаря дифференциальности вращения. Волны в такой ситуации переносят угловой момент, взаимодействуя с веществом диска. Эта проблема широко обсуждалась в приложении к галактикам [453,454,455].
В заключение отметим, что выбор механизма отвода углового момента (турбулентная вязкость или спиральные ударные волны) из АД на основе наблюдений в принципе возможен. Наибольшие различия должны возникать в ультрафиолетовой части спектра, однако могут быть обнаружены только достаточно сильные ударные волны [456].
<< 5.1 Осесимметричная дисковая аккреция | Оглавление | 5.3 Неустойчивости аккреционных ... >>