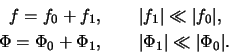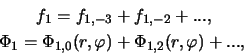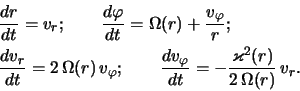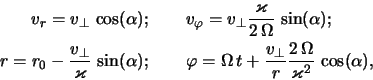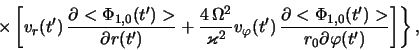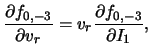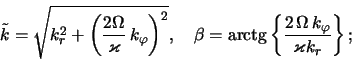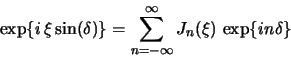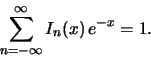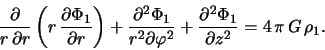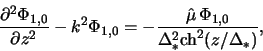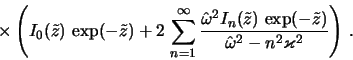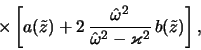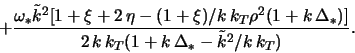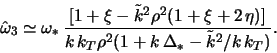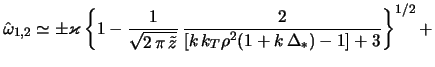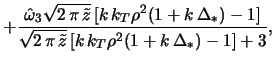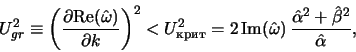Астронет: А. Г. Морозов, А. В. Хоперсков Физика Дисков http://variable-stars.ru/db/msg/1168623/node12.html

---

<< 2.1 Равновесие | Оглавление | 2.3 Гравитационная неустойчивость >>

Разделы

• 2.2.1 Постановка задачи
• 2.2.2 Возмущенная плотность звездного диска
• 2.2.3 Дисперсионное уравнение
• 2.2.4 Гравитационные и градиентные неосесимметричные возмущения

---

2.2 Динамика возмущений в плоскости диска

В предыдущем разделе построена модель стационарного равновесного звездного диска. Отклонения параметров диска (функции распределения, потенциала и др.) от равновесных значений будем называть возмущениями той или иной величины. Предположение о малой величине амплитуд отклонений от равновесного состояния весьма привлекательно для теоретического рассмотрения, поскольку исчезает одна из главных проблем при решении кинетического уравнения -- его нелинейность. Изучение возможных пространственных структур на фоне осесимметричного стационарного состояния весьма популярно. В то же время для реальных систем предположение о малой величине амплитуд возмущений часто нарушается. Достижения в построении нелинейных моделей (речь не идет о численных, см. гл. 3) невелики. Однако линейный подход позволяет весьма успешно решать классическую задачу об устойчивости равновесной системы, отвечая на вопрос о причинах роста со временем тех или иных первоначально сколь угодно малых по амплитуде возмущений. В основе анализа линейной устойчивости лежит дисперсионное уравнение, определяющее временную динамику малых возмущений в зависимости от их пространственной структуры. Из-за стационарности исходного диска возмущения пропорциональны и будущее системы определяется наличием и знаком мнимой части частоты (инкрементом). Рост со временем амплитуды в случае свидетельствует о неустойчивости системы.

В данном разделе мы получим дисперсионное уравнение, учитывающее неоднородность распределения равновесных параметров звездного диска.

2.2.1 Постановка задачи

Следуя Вандервоорту [192], получим кинетическое уравнение, описывающее динамику возмущений малой амплитуды в плоскости тонкого звездного диска. Для этого представим полные функции распределения звезд и гравитационный потенциал диска в виде суммы равновесных () и возмущенных () величин:

Линеаризованное по возмущенным величинам , кинетическое уравнение (2.1.7) в эпициклическом приближении имеет вид

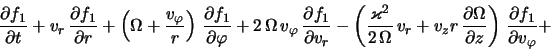
Для вычисления возмущенных величин , так же, как и при определении , , будем использовать приближение диска малой толщины ( ). Очевидно, что, как и равновесная , величина возмущенной поверхностной плотности . Поэтому возмущенная объемная плотность , и зависящая от -координаты часть возмущенного гравитационного потенциала пропорциональна . В соответствии с этим разложим , в ряды по степеням малого параметра [ср. с (2.1.18), (2.1.19)]:

где и . Тогда в рамках двух главных порядков по параметру уравнение (2.2.2) может быть расщеплено на систему двух уравнений

где операторы и определены соотношениями (2.1.23) и (2.1.17) соответственно.

Для решения этой системы так же, как и в п. 2.1.2, перейдем к переменным действие-угол , (2.1.25), (2.1.26). Поскольку , где , то

и уравнение (2.2.4) приобретает вид

Общее решение этого уравнения в случае, если равновесная функция распределения определена соотношением (2.1.44), можно записать в виде

где символ означает усреднение по фазе -движения:

Для определения величины усредним (2.2.5) по фазе -движения в соответствии с правилом (2.2.9). В результате получим

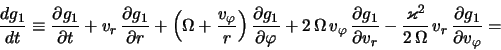
Структура этого уравнения не описывает эффекты, связанные с движением звезд по -координате. Тем самым удается сформулировать один из этапов решения задачи как задачу определения возмущенной функции распределения в модели тонкого ( ) звездного диска. Соответствующее вычисление величины , а затем и возмущенной объемной плотности диска конечной толщины проведено в следующем пункте.

2.2.2 Возмущенная плотность звездного диска

Уравнение (2.2.10) является линейным дифференциальным уравнением в частных производных. Его характеристики, определяющие невозмущенные траектории звезд в плоскости диска, описываются уравнениями

В рамках эпициклического приближения решение этих уравнений имеет вид

где , -- постоянные интегрирования, , , -- фаза движения звезды по эпициклической траектории ( -- начальная фаза). Из (2.2.12) нетрудно видеть, что невозмущенное движение звезды в эпициклическом приближении представляет собой движение по эллипсу (эпициклу), одна из полуосей которого, ориентированная на центр диска, равна , а другая, ориентированная в азимутальном направлении, равна . Центр этого эллипса (эпицикла) движется вокруг центра диска по круговой орбите радиусом с угловой скоростью .

Для вычисления возмущенной функции распределения запишем уравнение (2.2.10) в виде, удобном для применения в дальнейшем метода интегрирования по траекториям [193]:

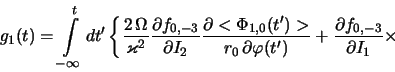
где ; -- интегралы движения звезды в плоскости диска в эпициклическом приближении и учтено, что [см. (2.1.31)]

Представление в виде (2.2.13) предполагает, что возмущение включается в момент времени с амплитудой пренебрежимо малой по сравнению с ее уровнем в момент времени .

Коэффициенты уравнения (2.2.10) в связи со стационарностью и осесимметричностью равновесного состояния диска не зависят явно от времени и азимутальной координаты. Это позволяет представить зависимость возмущенных величин , от времени и угла в экспоненциальном виде , где -- частота возмущений, -- номер моды по азимуту, -- азимутальное число. Такое представление, в частности, означает, что предполагавшийся выше при переходе от (2.2.10) к (2.2.13) рост амплитуды возмущений во времени эквивалентен наличию у частоты малой положительной мнимой части -- инкремента.

В радиальном направлении равновесный звездный диск неоднороден. Однако мы можем ограничиться рассмотрением коротковолновых в этом направлении возмущений -- таких, характерный масштаб изменения которых мал по сравнению с минимальным масштабом радиальной неоднородности диска. Роль последнего в галактиках за пределами их центральных областей обычно играет величина . Для изучения свойств таких возмущений используют ВКБ-приближение, в котором радиальная зависимость возмущенных величин полагается , где -- упоминавшийся выше характерный масштаб изменения возмущенных величин в радиальном направлении ( -- радиальное волновое число). Таким образом, сформулированное выше условие применимости ВКБ-приближения можно записать в виде^2.6

Такой подход позволяет преобразовать все дифференциальные операторы в подынтегральном выражении в (2.2.13) в алгебраические и тем самым связать величины , , алгебраическим уравнением

обычно называемым дисперсионным. Результаты его решения можно трактовать следующим образом. Возмущения, характеризуемые конкретными , , эволюционируют по закону , где -- вообще говоря, комплексная величина. И если корни дисперсионного уравнения (2.2.17) при некоторых значениях , таковы, что , то амплитуда таких возмущений экспоненциально растет со временем (вообще говоря, необязательно в каждой точке пространства). Заметим также, что, зная решения (2.2.17), мы в общем случае можем изучать и эволюцию произвольных возмущений, если в начальный момент времени нам будет известен фурье-спектр такого возмущения в -пространстве.

Для дальнейшего важно отметить, что мы не связываем решение рассматриваемой здесь задачи изучения динамики малых возмущений в звездном диске с исследованием поведения каких-либо глобальных структурных особенностей диска (например, спирального узора). Поэтому в отличие от подхода Лина и Шу [196,197] не будем пренебрегать в (2.2.10) и (2.2.13) возмущенными азимутальными силами. Такой подход позволяет нам изучить дисперсионные свойства неосесимметричных возмущений в неоднородном звездном диске и получить условие его устойчивости относительно неосесимметричных возмущений в его плоскости [198,199].

Вычислим фазу возмущений . Для этого перейдем в двумерном пространстве волновых векторов (, ) к величинам

здесь . Тогда с помощью уравнений (2.2.12), описывающих невозмущенные траектории звезд, нетрудно получить

Используя этот результат, приводим (2.2.13) к виду

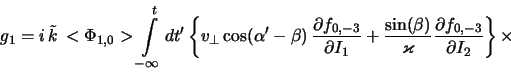
где ; ; . Затем с помощью разложения производящей функции [200]

в ряд по функциям Бесселя первого рода интегрируем (2.2.20) по времени . В результате получаем

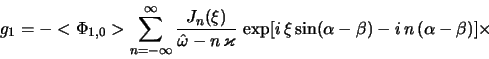
Объемная плотность диска, создаваемая возмущенной функцией распределения (2.2.8) с определяемой по (2.2.22) величиной , может быть получена интегрированием последней по пространству скоростей. В случае равновесного диска [см. (2.1.44)] эта операция с учетом разложения (2.2.21) приводит к следующему выражению:

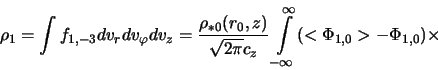
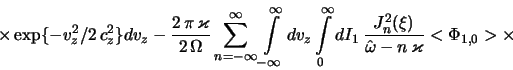
Поляченко и Фридман [1] показали, что возмущения в плоскости диска, исследованию свойств которых и посвящен этот раздел, в рамках линейной теории в модели тонкого диска отщепляются от изгибных (мембранных) колебаний диска. В последних локальная поверхностная плотность не возмущается, а возмущения объемной плотности имеют "дипольный" вид. Поэтому при описании свойств возмущений в плоскости диска в выражении (2.2.23) необходимо отбросить члены, не дающие вклада в возмущенную поверхностную плотность:

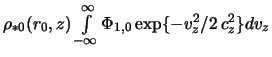Нетрудно видеть, что именно первый член в (2.2.23) не дает вклада в . Действительно, интегрируя по -координате с учетом (2.1.45) величину , получим

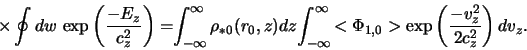
Для вычисления возмущенной объемной плотности, обусловленной вторым членом в (2.2.23), используем конкретный вид равновесной функции распределения звезд (2.1.44). Кроме того, в соответствии с данными наблюдений (см. разд. 1.1), показывающими, что характерные толщины звездных дисков галактик слабо меняются вдоль радиальной координаты, будем считать const. В этом случае с учетом (2.1.42) имеем три независимых параметра звездного диска, в качестве которых выберем величины , , . Тогда из (2.1.35)

Интегрируя затем (2.2.24) по , и отбрасывая в соответствии со сказанным выше члены, не дающие вклада в возмущенную поверхностную плотность диска, получим

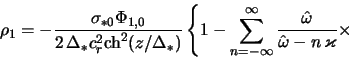
где ; -- модифицированные функции Бесселя первого рода,

и учтено, что [200]

2.2.3 Дисперсионное уравнение

Возмущения плотности диска приводят к возмущениям гравитационного потенциала , и связь между этими величинами определяется уравнением Пуассона [см. (2.1.3)]:

В рассматриваемом нами ВКБ-приближении это уравнение для гармоник возмущенного потенциала, характеризуемых волновым числом , приобретает вид

где величина определяется из (2.2.28) и тождества

Уравнение (2.2.34) похоже на уравнение Шредингера, описывающее движение частицы в потенциальной яме вдоль -координаты [201]. Однако для (2.2.34) задача поставлена несколько по-иному: для фиксированного значения "энергии" () необходимо найти "глубину потенциальной ямы" ( ), в которой может существовать заданный "уровень энергии" (). Нетрудно видеть, что минимальная глубина такой ямы определяется безузловой в -направлении собственной функцией

а соответствующее ей значение "глубины ямы" -- соотношением^2.7

Используя затем этот результат и определение по (2.2.28), (2.2.35), получаем искомое дисперсионное уравнение, описывающее динамику возмущений в звездном диске с волновым вектором, лежащим в его плоскости:

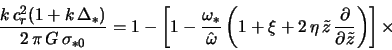
Нетрудно видеть, что это дисперсионное уравнение в пределе осесимметричных ( и, следовательно, ) возмущений в модели тонкого () диска тождественно совпадает с дисперсионным уравнением Лина и Шу [197] (см. также в монографии Фридмана и Поляченко [2]).

2.2.4 Гравитационные и градиентные неосесимметричные возмущения

Исследуем дисперсионные свойства возмущений, описываемых уравнением (2.2.38), частота которых в системе отсчета, вращающейся вместе с веществом диска, меньше эпициклической ( ). Для приближенного вычисления этих частот в (2.2.38) можно опустить члены ряда с . Упрощенное таким образом дисперсионное уравнение приобретает вид

где ; ; ; .

Если рассматривать только осесимметричные возмущения ( и, следовательно, ), то (2.2.39) описывает две гравитационные (джинсовские) ветви колебаний звездного диска, частоты которых различаются знаком:

В приближении тонкого () диска Тоомре было показано, что такие возмущения устойчивы [ ] при выполнении условия

В тонком диске, обладающем дисперсией радиальных скоростей , радиальный масштаб маргинально устойчивых осесимметричных возмущений может быть определен из соотношения

Учет стабилизирующего влияния конечной толщины звездного диска, предварительный анализ которого был проведен еще в работе Тоомре [202], показывает, что в рамках модели (2.1.44) такой диск устойчив при выполнении условия [192]

Перейдем к изучению спектра неосесимметричных возмущений. Предварительно заметим, что . С учетом того, что для наиболее близких к порогу неустойчивости возмущений в маргинально устойчивом по Тоомре-Вандервоорту диске , а также условия (2.2.16) это означает, что для таких возмущений

В длинноволновой части спектра () в маргинально устойчивом по Тоомре диске условие (2.2.44) тоже выполняется и, следовательно, эффекты неоднородности диска малы. В этом пределе законы дисперсии двух гравитационных ветвей колебаний звездного диска согласно (2.2.39) имеют вид

Кроме этих ветвей дисперсионное уравнение (2.2.39) предсказывает существование еще одной -- градиентной ветви^2.8 неосесимметричных возмущений, закон дисперсии которой имеет вид

По порядку величины в длинноволновой () области ; .

В коротковолновой же части спектра (), используя асимптотику модифицированных функций Бесселя, из (2.2.39) получим

В этой области длин волн тоже ; .

Таким образом, как в длинноволновой, так и в коротковолновой частях спектра градиентная ветвь является низкочастотной и хорошо отделена от гравитационных ветвей. Все три ветви в этих частях спектра оказываются устойчивыми в маргинально устойчивом относительно осесимметричных возмущений диске.

Иной результат получается в промежуточной области длин волн . Чтобы продемонстрировать это, рассмотрим простую модель тонкого () твердотельно вращающегося ( ) неоднородного диска, в котором (тем самым масштабы неоднородностей и одинаковы и, следовательно, ). В малой окрестности маргинально устойчивых по Тоомре возмущений с [см.(2.2.42)] дисперсионное уравнение (2.2.39) принимает вид

где ; ; , а величина в соответствии с данными наблюдений полагалась убывающей к периферии диска. В (2.2.49) мы ограничились разложением членов уравнения (2.2.39) в ряды по степеням до второй включительно, имея в виду кроме вычисления частот колебаний диска определить еще и тип неустойчивости.

Полагаем диск слабонеоднородным: . Тогда в главном порядке по из (2.2.49) для частот колебаний диска следует

Неустойчивость рассматриваемой модели в области джинсовских длин волн () очевидна. В чем же ее причина?

Известно, что в маргинально устойчивом по Тоомре диске в окрестности точки частоты обеих гравитационных ветвей осесимметричных возмущений пропорциональны . Ясно, что в некоторой малой (в силу ) окрестности частота градиентных возмущений окажется сравнимой с частотой одной из гравитационных ветвей неосесимметричных возмущений. Тогда взаимовлияние этих ветвей, искажая спектры возмущений, приведет к неустойчивости неосесимметричных возмущений. Таким образом, причиной гравитационно-градиентной неустойчивости (2.2.50) является неоднородность диска. Природа же этой неустойчивости, очевидно, гравитационная.

Гравитационно-градиентная неустойчивость принадлежит к типу "абсолютных", т.е. таких, при возбуждении которых амплитуда возмущений растет в каждой точке пространства, движущейся вместе с веществом диска. Действительно, неустойчивость является "абсолютной", а не "конвективной" (в этом случае неустойчивое возмущение сносится течением так быстро, что в каждой точке пространства возмущения со временем стремятся к нулю), если выполняется условие [203]

где ; . Нетрудно видеть, что для возмущений с и . Тем самым условие (2.2.52) для гравитационно-градиентной неустойчивости выполняется.

Впервые градиентная ветвь была получена Хантером [204] в модели холодного () гравитирующего диска. Описанные здесь результаты относятся к достаточно горячему ( ) бесстолкновительному диску. Тем не менее результат Хантера вытекает из дисперсионного уравнения (2.2.38) при выполнении цепочки неравенств (в реальных системах ).

---

<< 2.1 Равновесие | Оглавление | 2.3 Гравитационная неустойчивость >>