Полный Архив предыдущих выпусков обзоров astro-ph.
Полезные астрономические ссылки.
Короткое эссе об электронных препринтах.
Обзорные статьи в astro-ph с 2001 г.
Авторы проекта
Сергей Попов
Михаил Прохоров
Новостные ленты
Новости астрономии от ПРАО
Текущие открытия в ФЭЧ
Новости космонавтики
Новости от УФН
Информнаука
Перст
Подписка на рассылку обзоров на Subscribe.Ru
31.08.2003. Где находится последняя устойчивая круговая орбита в сверхкритических аккреционных потоках?
из работы Кен-я Ватараи и Шина Минешиги (Ken-ya Watarai, Shin Mineshige)
astro-ph/0308391
В ньютоновских полях тяготения любые круговые (и не только круговые) орбиты устойчивы. Т.е. без дополнительных воздействий (атмосфера, приливы и т.п.) тело может вращаться сколь угодно долго на орбите любого радиуса. Для шварцшильдовской черной дыры это уже не так. Круговые орбиты с радиусом меньшим 3rg становятся неустойчивыми (rg=2GM/c2 т.н. гравитационный, или шварцшильдовский, радиус. Фактически именно его в популярной литературе чаще всего называют "радиус черной дыры"). У вращающихся (керровских) черных дыр круговые орбиты возможны только в плоскости их экватора. Для этих черных дыр также существует граница устойчивости орбит, но радиус последней устойчивой круговой орбиты зависит от углового момента черной дыры и от направления движения частицы по орбите: орбиты частиц движущихся в сторону вращения черной дыры остаются устойчивыми на более близких расстояниях, чем в шварцшильдовском случае, а при противоположно направлении движения теряют устойчивость при r>3rg. Существование устойчивой круговой орбиты хорошо иллюстрирует эффективный потенциал - зависимость от радиуса энергии частицы с фиксированным моментом импульса. Круговая орбита проходит там, где на эффективном потенциале расположен минимум. Если же минимума нет (потенциал имеет "гладкую" форму), то круговые орбиты с данным моментом неустойчивы.
А как ведет себя вещество в аккреционных дисках вокруг черных дыр. Обычно полагают, что внутренний край диска совпадает с последней устойчивой орбитой. Однако, считать частицы вещества в диске свободными уже нельзя: на них действуют вязкие силы от соседних частиц и градиент давления. Это не отменяет само существование границы между устойчивыми и неустойчивыми орбитами, но смещает ее положение. Особенно сильны эти эффекты в сверхкритических дисках (когда темп втока вещества, например, от второй звезды в двойной системе, очень велик). Во внутренних частях таких дисков важную роль играет не только газовое давление, но и давление излучения.
Авторы данной работы численными методами показали, что при высоких темпах аккреции
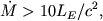
(здесь LE - Эддингтоновская светимость) в эффективном
потенциале исчезает минимум, причем этот эффект сохраняется даже при
слабой вязкости
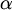 ~0.01,
поскольку основную роль в
нем играет градиент давления.
~0.01,
поскольку основную роль в
нем играет градиент давления.
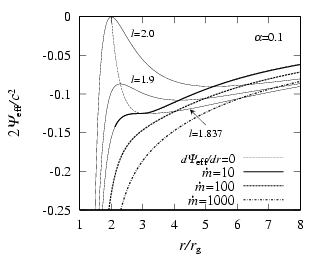
На рисунке вверху показаны профили эффективного потенциала для
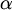 =0.1.
Толстые линии (сплошная, штриховая и точечная) показывают рассчитанные
профили для темпов аккреции равных, соответственно, 10, 100 и 1000
Эддингтоновских.
(Эддингтоновский темп аккреции равен LE/c2.)
Тонкие линии показывают аналитические профили эффективных потенциалов для
одиночных частиц с заданным моментом импульса
l/rgc = 2.0, 1.9 и 1.837 (последнее значение
соответствует пределу устойчивости круговых орбит).
=0.1.
Толстые линии (сплошная, штриховая и точечная) показывают рассчитанные
профили для темпов аккреции равных, соответственно, 10, 100 и 1000
Эддингтоновских.
(Эддингтоновский темп аккреции равен LE/c2.)
Тонкие линии показывают аналитические профили эффективных потенциалов для
одиночных частиц с заданным моментом импульса
l/rgc = 2.0, 1.9 и 1.837 (последнее значение
соответствует пределу устойчивости круговых орбит).