Уважаемые коллеги!
Нужен совет относительно того возможно ли взять интеграл и как это сделать:

Нажмите для просмотра прикрепленного файла

Спасибо заранее.

Ухх, кто же таким злобным образом картинки-то выкладывает. Тьфу!

Скорее всего, аналитически так просто не берется, а при определенных соотношениях параметров и вовсе расходится. Если же все хорошо в этом плане, то основная надежда на что-нибудь типа вычетов, но я без понятия, как тут контур организовать, особенно с учетом того, что по левому пределу интеграл несобственный. Хотя леший его знает, вдруг и можно накреативить что-нибудь безумное (ну, не знаю, оттянуть левый предел какой-то очень хитрой заменой на минус бесконечность и сварганить с помощью леммы Жордана, хотя это только на словах).

Если Вы мне таки объясните, как тут формулами пользоваться, буду признательна


У меня пока основная надежда на справочник по интегралам

>Если Вы мне таки объясните, как тут формулами пользоваться, буду признательна

Вот так, например:



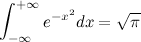
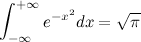
PS Картинка не очень няшная вышла, но что-то лень возиться, при желании можно и покрасивей сделать, тут больших проблем нет.

Тег [img] + онлайн-сервисы рулят.

>У меня пока основная надежда на справочник по интегралам

Это вряд ли, боюсь... Я насчет экспонент с корнями ничего толкового вообще не припомню.

Вряд ли такой интеграл берется аналитически. Это-то и хорошо. Функцию f(a,b ) можно назвать спецфункцией Дженни, а исследование ее свойств назвать серьезной наукой. Опасности, что она вдруг потом выразится через какую-нибудь пошлость вроде элементарных функций, практически никакой.