Мы рассмотрели пока лишь вопрос о траектории луча в оптически неоднородной среде и сформулировали алгоритм расчета этой траектории. Теперь рассмотрим, как определяется траектория материальной точки массы m, движущейся в потенциальном поле U(x, y, z). Ее полная энергия складывается из кинетической и потенциальной и сохраняется (в силу закона сохранения энергии) в процессе движения
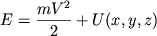 , , | (6) |
где V - абсолютная величина мгновенной скорости.
Напомним, что потенциальная энергия определяется как работа по перемещению тела из данного положения в некоторую другую точку, в которой потенциальная энергия принимается за нуль. В простейшем, известном из школьного курса случае для потенциальной энергии в однородном поле тяжести имеем
U(z) = mgz.
Здесь координата z определяет высоту подъема над поверхностью Земли, принимаемую за уровень, для которого потенциальная энергия полагается равной нулю. Более точное выражение для потенциальной энергии тела над поверхностью Земли следует из закона всемирного тяготения
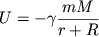 , , | (8) |
где 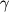 - постоянная всемирного тяготения, m - масса тела, M - масса Земли, R - радиус Земли, r - расстояние от поверхности Земли. В данном случае нуль потенциальной энергии выбирается в бесконечно удаленной точке.
Для нас будет важно в дальнейшем, что при движении в потенциальном поле при заданном начальном значении энергии абсолютная величина скорости однозначно определяется, согласно (6), положением материальной точки в пространстве: - постоянная всемирного тяготения, m - масса тела, M - масса Земли, R - радиус Земли, r - расстояние от поверхности Земли. В данном случае нуль потенциальной энергии выбирается в бесконечно удаленной точке.
Для нас будет важно в дальнейшем, что при движении в потенциальном поле при заданном начальном значении энергии абсолютная величина скорости однозначно определяется, согласно (6), положением материальной точки в пространстве:
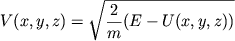 . . | (9) |
Для простоты дальнейшего изложения рассмотрим случай, когда сила, действующая на материальную точку, всюду имеет одинаковое направление, как в первом примере, но может изменяться по величине, как во втором примере. В этом случае потенциальная энергия будет зависеть только от одной координаты, которая отсчитывается вдоль направления, по которому направлена сила.
Аналогично тому, как мы делали при рассмотрении траектории луча, разобьем пространство на слои в направлении, перпендикулярном направлению силы. В каждом слое скорость материальной точки будем считать приближенно постоянной.
Пусть материальная точка массы m, имеющая скорость 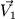 , пересекает границу первого и второго слоев. Во втором слое скорость частицы , пересекает границу первого и второго слоев. Во втором слое скорость частицы 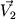 . Согласно второму закону Ньютона, . Согласно второму закону Ньютона,
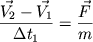 , , | (10) |
где 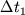 - время прохождения первого слоя.
Заметим, что, согласно (10), составляющая скорости, перпендикулярная силе, не изменяется. Поэтому движение частицы будет происходить в одной плоскости, проходящей через направление начальной скорости и направление силы. Это утверждение представляет собой аналог первой части закона преломления.
Выберем в плоскости движения декартову систему координат (x, y), причем ось Oy выберем вдоль направления силы. Тогда из (10) следует - время прохождения первого слоя.
Заметим, что, согласно (10), составляющая скорости, перпендикулярная силе, не изменяется. Поэтому движение частицы будет происходить в одной плоскости, проходящей через направление начальной скорости и направление силы. Это утверждение представляет собой аналог первой части закона преломления.
Выберем в плоскости движения декартову систему координат (x, y), причем ось Oy выберем вдоль направления силы. Тогда из (10) следует
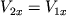 , , |
(11) |
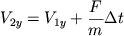 , , |
где V1x , V1y , V2x , V2y - проекции скорости в первом и втором слоях на выбранные оси координат, F - составляющая силы вдоль оси Oy. Первое уравнение (11) можно заменить на
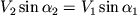 , , | (12) |
где 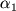 и и 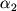 - углы, которые образуют скорости в первом и втором слоях с направлением силы. А это как раз аналог второй части закона преломления, выражаемой формулой (1а).
Напомним еще раз, что в каждом слое абсолютная величина скорости однозначно определена. Поэтому угол - углы, которые образуют скорости в первом и втором слоях с направлением силы. А это как раз аналог второй части закона преломления, выражаемой формулой (1а).
Напомним еще раз, что в каждом слое абсолютная величина скорости однозначно определена. Поэтому угол 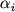 , под которым скорость направлена к действующей силе в каждом слое, может быть найден с помощью закона преломления (12) по углу , под которым скорость направлена к действующей силе в каждом слое, может быть найден с помощью закона преломления (12) по углу 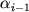 . Таким образом, для определения траектории материальной точки получается тот же алгоритм, что и для определения траектории луча (рис. 4). . Таким образом, для определения траектории материальной точки получается тот же алгоритм, что и для определения траектории луча (рис. 4).
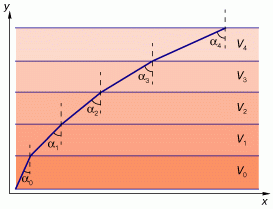 |
| Рис. 4. Построение траектории движения материальной точки методом геометрической оптики. Каждый слой характеризуется определенным значением скорости Vi. Угол падения для i-го слоя находится по углу падения для (i-1)-го слоя с помощью закона преломления (12)
|
Отметим, что роль показателя преломления в рассматриваемом случае играет величина скорости. Очевидно, что траектория луча и траектория частицы будут в точности совпадать, если показатель преломления пропорционален скорости и направление луча в начальной точке совпадает с направлением скорости. Согласно (9), первое условие может быть выражено равенством
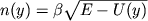 , , | (13) |
где 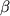 - произвольный положительный коэффициент пропорциональности.
Если мы хотим найти одно из возможных потенциальных полей, в котором частица движется по такой же траектории, что и луч в заданной неоднородной среде, то это проще сделать для случая E = 0. Тогда - произвольный положительный коэффициент пропорциональности.
Если мы хотим найти одно из возможных потенциальных полей, в котором частица движется по такой же траектории, что и луч в заданной неоднородной среде, то это проще сделать для случая E = 0. Тогда
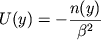 . . | (14) |
При этом потенциальная энергия U(y) должна быть отрицательной. Величина 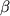 произвольна. Из сказанного выше следует, что она не должна влиять на траекторию. На что же она влияет? Так как показатель преломления является безразмерной величиной, то очевидно, что произвольна. Из сказанного выше следует, что она не должна влиять на траекторию. На что же она влияет? Так как показатель преломления является безразмерной величиной, то очевидно, что 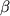 зависит от выбираемой единицы энергии. Если масштаб координаты фиксирован, то изменение единиц энергии можно достичь изменяя единицы массы и времени. Таким образом, изменение зависит от выбираемой единицы энергии. Если масштаб координаты фиксирован, то изменение единиц энергии можно достичь изменяя единицы массы и времени. Таким образом, изменение 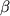 можно интерпретировать как переход к случаям движения частиц с другими массами или при фиксированной массе в другом масштабе времени (быстрее или медленнее). При определенном выборе единиц величину можно интерпретировать как переход к случаям движения частиц с другими массами или при фиксированной массе в другом масштабе времени (быстрее или медленнее). При определенном выборе единиц величину 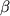 можно положить равной 1.
Таким образом, сформулированная выше оптико-механическая аналогия доказана. Правда, она доказана для случая силы, имеющей постоянное направление в пространстве. Но это не умаляет общности результата, поскольку в достаточно малой окрестности направление силы можно считать фиксированным, а оптическую среду - слоисто-однородной.
Мы не будем углубляться в подробности геометрической оптики и классической механики, чтобы не затушевать главный результат, заключающийся в том, что классическую механику можно рассматривать как аналог геометрической оптики. Это открытие У.Р. Гамильтона объяснило, в частности, почему волновая теория Гюйгенса и корпускулярная теория Ньютона одинаково хорошо описывали явления отражения и преломления света. Отметим только, что еще до работ Гамильтона начиная с XVII века настойчивые поиски оптико-механической аналогии такими выдающимися учеными, как Р. Декарт, П. Ферма, Х. Гюйгенс, И. Ньютон и др., способствовали активному развитию как оптики, так и классической механики [Меркин Д.Р.,1994, Л.С. Полак, 1959]. Так, известный вариационный принцип Ферма в оптике был использован Я. Бернулли для формулировки первого вариационного принципа в механике, что в конце концов привело к созданию такой важной области математики, как вариационное исчисление. Подробнее мы расскажем об этом в другой статье.
Гамильтон не только установил конструктивную связь между геометрической оптикой и классической механикой, но и выяснил соответствие между геометрической оптикой и волновой оптикой. К сожалению, первоначально работы Гамильтона были опубликованы в малоизвестных "Трудах Ирландской академии наук", и поэтому идеи Гамильтона не сразу оказали влияние на развитие физики. Только немногие из английских физиков, в частности Дж.К. Максвелл и Рэлей, знали работы Гамильтона по оптике и применяли его методы. Фактически в исследованиях Гамильтона содержалось предсказание возможности волновой механики. В 20-х годах нашего века эти идеи Гамильтона были развиты Луи де Бройлем и Э. Шредингером при создании концепции корпускулярно-волнового дуализма, что в итоге привело к созданию современной квантовой механики. можно положить равной 1.
Таким образом, сформулированная выше оптико-механическая аналогия доказана. Правда, она доказана для случая силы, имеющей постоянное направление в пространстве. Но это не умаляет общности результата, поскольку в достаточно малой окрестности направление силы можно считать фиксированным, а оптическую среду - слоисто-однородной.
Мы не будем углубляться в подробности геометрической оптики и классической механики, чтобы не затушевать главный результат, заключающийся в том, что классическую механику можно рассматривать как аналог геометрической оптики. Это открытие У.Р. Гамильтона объяснило, в частности, почему волновая теория Гюйгенса и корпускулярная теория Ньютона одинаково хорошо описывали явления отражения и преломления света. Отметим только, что еще до работ Гамильтона начиная с XVII века настойчивые поиски оптико-механической аналогии такими выдающимися учеными, как Р. Декарт, П. Ферма, Х. Гюйгенс, И. Ньютон и др., способствовали активному развитию как оптики, так и классической механики [Меркин Д.Р.,1994, Л.С. Полак, 1959]. Так, известный вариационный принцип Ферма в оптике был использован Я. Бернулли для формулировки первого вариационного принципа в механике, что в конце концов привело к созданию такой важной области математики, как вариационное исчисление. Подробнее мы расскажем об этом в другой статье.
Гамильтон не только установил конструктивную связь между геометрической оптикой и классической механикой, но и выяснил соответствие между геометрической оптикой и волновой оптикой. К сожалению, первоначально работы Гамильтона были опубликованы в малоизвестных "Трудах Ирландской академии наук", и поэтому идеи Гамильтона не сразу оказали влияние на развитие физики. Только немногие из английских физиков, в частности Дж.К. Максвелл и Рэлей, знали работы Гамильтона по оптике и применяли его методы. Фактически в исследованиях Гамильтона содержалось предсказание возможности волновой механики. В 20-х годах нашего века эти идеи Гамильтона были развиты Луи де Бройлем и Э. Шредингером при создании концепции корпускулярно-волнового дуализма, что в итоге привело к созданию современной квантовой механики.
Написать комментарий
|

