Предыдущая: Кто же прав?

Образование двойных звезд

Звезды образуются из газа и пыли вследствие гравитационной неустойчивости. В применении к Солнцу эта идея на гуманитарном уровне была высказана еще Иммануилом Кантом в 1755 г. и поддержана позднее Лапласом. Образование звезд "окутано туманом", но лишено всякой "чертовщины". "Туман" появляется оттого, что сжимающееся облако газа непрозрачно для электромагнитных волн. Противники этой гипотезы часто в качестве аргумента высказывали тезис, что, мол, никто никогда не видел сжатия облаков газа, а наоборот, всюду наблюдаются сплошные взрывы. Здесь работает мощный эффект селекции. Звезды образуются в местах, где много газа и пыли. Но именно там видимость особенно плохая. Впрочем, в последние годы, когда появились мощные инфракрасные телескопы - ученые уже "воочию" увидели сжатие облаков. Что же заставляет сжиматься облака газа? На этот вопрос строгий математический ответ дал английский астроном Джеймс Джинс в начале XX века. Допустим, что бесконечное пространство заполнено однородным газом. Возмутим слегка параметры газа в какой-нибудь малой области, например слегка сожмем газ. Если бы не было гравитации, сжатие сменилось бы расширением, возмущая соседние участки газа. По газу побежала бы волна возмущений - звук. В межзвездном пространстве размеры облаков велики, и наряду с силами давления, большую роль начинают играть силы гравитации. Выделим из межзвездной среды шарообразную область и слегка ее сожмем. Сила, с которой облако притягивает само себя, пропорциональна 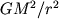(М и r - масса и радиус облака). Внешние силы не учитываются, так как они взаимно компенсируют друг друга. 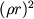Значит, давление силы гравитации пропорционально (см. примечание). А давление одноатомного газа при адиабатическом сжатии зависит от плотности по закону 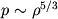. Отсюда видно, что если мы будем брать все большее и большее облако, то сила гравитации при некотором r станет больше силы давления газа и облако неминуемо начнет сжиматься. Этот процесс называется джинсовской неустойчивостью.

Минимальный размер, начиная с которого облако становится неустойчивым по отношению к сжатию, называется джинсовской длиной волны. "Волны" - потому, что точный ответ получается при решении задачи о распространении волн в самогравитирующем газе. Приближенно джинсовскую длину можно найти, приравняв давление газа в шаре радиуса r давлению силы гравитации. Давление газа вычисляется по формуле Менделеева-Клапейрона. Давление сил гравитации прикинем мысленно, разделив шар пополам и вычислив силу притяжения двух половинок друг к другу. Итак, получаем примерное равенство

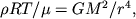
из которого находим приближенное значение джинсовской длины волны:

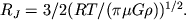
Здесь Т - температура газа, R - газовая постоянная, 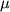- молекулярная масса газа.

Конечно, газ в Галактике распределен отнюдь не однородно. Как выяснилось в конце 70-х годов, почти весь газ сосредоточен в гигантских молекулярных облаках с массами в сотни тысяч и миллионы масс Солнца. Почему, спрашивается, из одного облака не образуется одна гигантская звезда? Потому, что и облака неоднородны: звездообразование идет в самых плотных центральных частях этих облаков. Кроме того, в облаках газ не покоится, а участвует в различных хаотических движениях. Такие движения называются турбулентностью. Отдельные ячейки облака вращаются в различных направлениях. Причем вихри встречаются на всех масштабах - от размера самого облака до самых малых его частей.

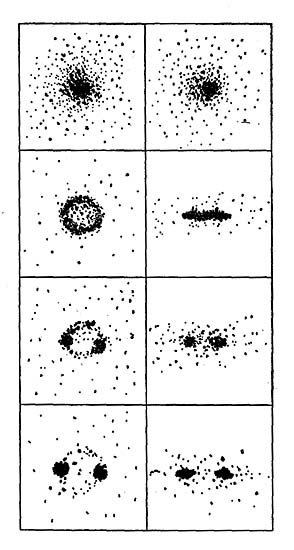
Рис. 17 Возможная картина образования двойной системы из вращающегося облака, вид с полюсов (слева) и с экватора вращения (справа).

Итак, турбулентность, по-видимому, является причиной возникновения двойных систем. Результаты расчетов, проведенных на самых крупных вычислительных машинах, качественно представлены на рис. 17. Облако вначале сжимается по оси вращения, а потом превращается в тор. Тор разбивается на отдельные сгустки, из которых и образуются двойные звезды. На самом деле часто образуются системы не двух, а большего числа звезд (кратные звезды). В Галактике очень много кратных звезд. Наша книга посвящена двойным звездам, хотя звезды, о которых мы будем говорить, могут быть, например, и тройными. Это упрощение вполне оправдано Нас будет интересовать кратность системы только с точки зрения влияния звезд друг на друга. Природа так устроена, что любая кратная система в этом смысле сводится к двойной. Три звезды не могут устойчиво существовать совместно и равноправно. Система, состоящая из трех звезд, расстояния между которыми сравнимы друг с другом, рано или поздно выбрасывает из себя одну из звезд. Виной этому своеобразный кумулятивный эффект, известный из гидродинамики. Он применялся в годы войны в специальных противотанковых снарядах. Суть его иллюстрируется опытом Покровского.

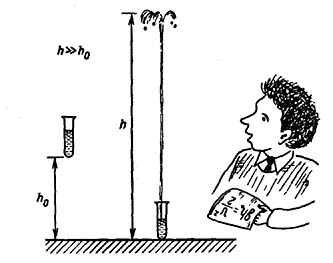
Возьмите пробирку, наполненную водой. Если вертикально сбросить ее на пол с небольшой высоты (например, несколько дециметров), то из нее вырвется струя воды, направленная вверх на несколько метров (рис. 18).

Рис. 18. Опыт Покровского, иллюстрирующий кумулятивный эффект

Кажется, не выполняется закон сохранения энергии. В действительности с энергией все в порядке. Просто происходит перераспределение энергии и импульса между частями воды. Большая часть воды остается в пробирке, вообще не выливаясь, а свою кинетическую энерию передает меньшей части воды, которая поднимается на высоту, много большую начальной.

С кумулятивным эффектом нам приходится сталкиваться в метро. Инженер, спроектировавший разменный автомат, четко согласовал высоту, с которой падают пятачки, с высотой окошечка, откуда мы их берем. Каждый отдельный пятачок не в состоянии перелететь через заградительную стенку, не хватит начальной потенциальной энергии. Тем не менее, пятачки время от времени вылетают на пол. Виной тому тот же кумулятивный эффект. Вылетевший на пол пятачок отобрал часть импульса у своих соседей. Чем больше монет, тем легче это делать. Именно поэтому чаще приходится нагибаться после размена двадцатикопеечных монет.

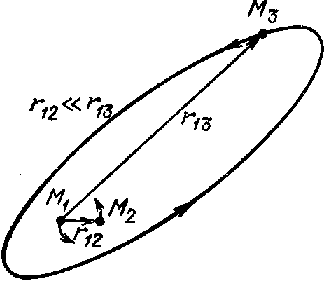
Рис. 19. В тройных системах расстояние между двумя звездами, как правило, много меньше расстояния до третьей.

В результате кумулятивного эффекта система либо становится двойной, либо остается тройной, но при этом одна из звезд движется по орбите на расстоянии, много большем, чем расстояние между близкими звездами. Наиболее существенным оказывается притяжение двух близких звезд. Поэтому кратные системы сводятся к двойным (рис. 19).

Примечание: Действительно, заметив, что 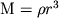, получаем для давления силы гравитации .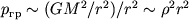

Продолжение следует

Обозрение "Физические явления на небесах" профессора В.М.Липунова.