Ионная связь характерна для соединений, у которых один элемент является металлом, а другой близок к последней группе Периодической системы элементов, например для щелочно-галоидных соединений (NaCl, KBr, LiF) ионная связь представляет собой кулоновское взаимодействие разноименно заряженных ионов. Однако электростатические силы не в состоянии удержать систему в равновесии, поэтому ионная связь никогда не бывает "чистой". При сближении ионов возникают силы отталкивания неэлектростатической природы. Это квантовомеханические силы, обусловленные принципом Паули.
Согласно этому фундаментальному принципу квантовой механики, два электрона с одинаково направленными спинами (спин - внутренняя квантовая степень свободы, собственный момент вращения частицы) не могут находиться в одном и том же квантовом состоянии, то есть на одном и том же энергетическом уровне. Поэтому электронные оболочки атомов не могут проникать друг в друга, они отталкиваются. Общий характер зависимости энергии связи от межатомного расстояния для ионного типа связи показан на рис. 1. Такой вид энергии означает, что на больших расстояниях между атомами действуют силы притяжения, медленно стремящиеся к нулю при 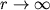 (кулоновское притяжение разноименных ионов), а на достаточно близких расстояниях превалируют силы отталкивания, быстро стремящиеся к бесконечности при (кулоновское притяжение разноименных ионов), а на достаточно близких расстояниях превалируют силы отталкивания, быстро стремящиеся к бесконечности при 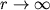 (квантовомеханические силы, определяемые принципом Паули). r0 определяет положение устойчивого равновесия и является постоянной решетки. (квантовомеханические силы, определяемые принципом Паули). r0 определяет положение устойчивого равновесия и является постоянной решетки.
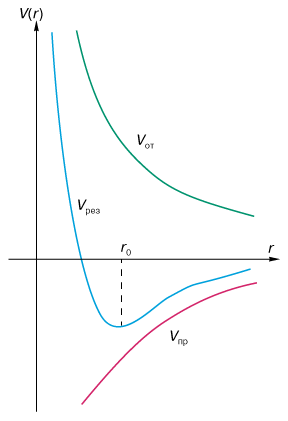 |
Рис. 1. Энергия связи ионного соединения. Vрез(r) - результирующая энергия связи, Vот - энергия отталкивания, Vпр - энергия притяжения, r0 - равновесное межатомное расстояние, соответствующее минимуму энергии связи.
|
Даже в тех атомах и молекулах, электрический дипольный момент которых равен нулю, будет существовать флуктуирующий дипольный момент, связанный с мгновенным положением электрона в атоме. Мгновенное электрическое поле, связанное с этим моментом, приведет к возникновению индуцированного дипольного момента в соседних атомах. В среднем взаимодействие дипольного момента исходного атома с индуцированными дипольными моментами соседних атомов приведет к притяжению между атомами, что выгодно энергетически, так как понижается энергия системы. Энергия ван-дер-ваальсова взаимодействия убывает с расстоянием как 1/r6: случайно возникший дипольный момент 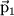 создает электрическое поле создает электрическое поле 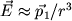 . Это поле поляризует соседний атом, создавая диполь . Это поле поляризует соседний атом, создавая диполь 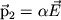 ( (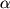 - диэлектрическая восприимчивость). Энергия взаимодействия этих диполей равна потенциальной энергии диполя - диэлектрическая восприимчивость). Энергия взаимодействия этих диполей равна потенциальной энергии диполя 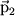 в поле в поле 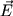 , , 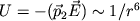 . Более строгий квантовомеханический расчет приводит к тому же результату.
Величина энергии связи для кристаллов с ван-дер-ваальсовым взаимодействием на один-два порядка меньше, чем у ионных, поэтому соответствующие вещества имеют низкую точку плавления и кипения. Ван-дер-ваальсова связь преобладает в благородных газах, кристаллизующихся при температурах порядка 10-100 K, в молекулярных кристаллах, которые построены не из отдельных атомов, а из молекул. Таковыми являются водород, в узлах решетки которого находятся молекулы H2, фуллерены - кристаллы, состоящие из молекул, содержащих шестьдесят атомов углерода (C60), и др.
Классический пример ковалентной связи - молекула водорода H2 (два электрона и два протона), главную роль в образовании которой играют обменные силы. Это силы квантовомеханической природы. Возникают они из-за того же самого кулоновского взаимодействия электронов и принципа Паули, учитывающего корреляцию в движении электронов, обусловленную наличием спина. Уравнение Шредингера для молекулы водорода имеет два решения: симметричное относительно перестановки координат электронов (замена местами), соответствующее состоянию с антипараллельными спинами электронов и антисимметричное, когда спины параллельны. Энергия взаимодействия, соответствующая каждому из этих решений, показана на рис. 2, а. Устойчивое состояние молекулы получается только для симметричного решения (связующее состояние). На рис. 2, б показано распределение плотности электронов в молекуле водорода. Плотность электронов в центре линии, соединяющей оба ядра в случае симметричного решения, наибольшая, а в случае антисимметричного обращается в нуль. Симметричное (связующее) состояние энергетически более выгодно, так как электроны одновременно взаимодействуют с обоими ядрами и за счет этого понижается энергия системы. . Более строгий квантовомеханический расчет приводит к тому же результату.
Величина энергии связи для кристаллов с ван-дер-ваальсовым взаимодействием на один-два порядка меньше, чем у ионных, поэтому соответствующие вещества имеют низкую точку плавления и кипения. Ван-дер-ваальсова связь преобладает в благородных газах, кристаллизующихся при температурах порядка 10-100 K, в молекулярных кристаллах, которые построены не из отдельных атомов, а из молекул. Таковыми являются водород, в узлах решетки которого находятся молекулы H2, фуллерены - кристаллы, состоящие из молекул, содержащих шестьдесят атомов углерода (C60), и др.
Классический пример ковалентной связи - молекула водорода H2 (два электрона и два протона), главную роль в образовании которой играют обменные силы. Это силы квантовомеханической природы. Возникают они из-за того же самого кулоновского взаимодействия электронов и принципа Паули, учитывающего корреляцию в движении электронов, обусловленную наличием спина. Уравнение Шредингера для молекулы водорода имеет два решения: симметричное относительно перестановки координат электронов (замена местами), соответствующее состоянию с антипараллельными спинами электронов и антисимметричное, когда спины параллельны. Энергия взаимодействия, соответствующая каждому из этих решений, показана на рис. 2, а. Устойчивое состояние молекулы получается только для симметричного решения (связующее состояние). На рис. 2, б показано распределение плотности электронов в молекуле водорода. Плотность электронов в центре линии, соединяющей оба ядра в случае симметричного решения, наибольшая, а в случае антисимметричного обращается в нуль. Симметричное (связующее) состояние энергетически более выгодно, так как электроны одновременно взаимодействуют с обоими ядрами и за счет этого понижается энергия системы.
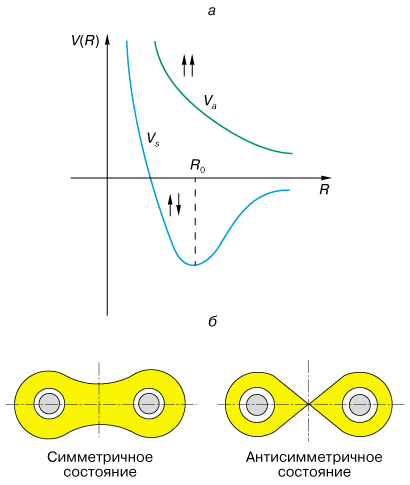 | Рис. 2. а - энергия связи молекулы водорода для состояний с параллельными и антипараллельными спинами; б - распределение электронной плотности в молекуле водорода для состояний с антипараллельными и параллельными спинами.
|
Для состояния, когда спины антипараллельны, происходит взаимная компенсация спинов внешних валентных электронов. Таким образом, при образовании молекулы электроны во внешних оболочках атомов перестраиваются так, что валентности атомов насыщаются, так как насыщение валентностей состоит во внешней компенсации спинов валентных электронов, поэтому химическую валентность следует определять числом электронов внешней оболочки с нескомпенсированным спином. По этой причине благородные газы не могут образовывать ковалентных кристаллов - обмена электронов с другими атомами нет, так как электронные оболочки заполнены полностью.
Классическим примером ковалентных кристаллов являются полупроводники алмаз, кремний, германий. У углерода есть два электрона в s-состоянии, два в р-состоянии. При сближении атомов электронные оболочки перестраиваются так, что все четыре электрона становятся неспаренными. Распределение электронной плотности оказывается сильно неоднородным, направленным и обладает тетраэдрической симметрией, характерной для структуры данных кристаллов. В полупроводниковых соединениях элементов III и V групп, а также II и VI групп Периодической системы, таких, как GaAs, ZnS, межатомная связь представляет уже смесь ковалентной и ионной составляющих.
В металлах много свободных электронов. Электроны могут перемещаться с одного атома на другой. Связь между атомами кристалла становится коллективизированной. Поэтому в простейшем случае металлическую связь можно рассматривать или как предел ковалентной связи, или как предел ионной (например, металлический натрий можно представить как Na++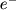 ). При всей искусственности такого подхода в этом есть что-то полезное. Рис. 3 демонстрирует распределение плотности электронного заряда в кристаллах с различным типом связи и переход от ковалентной связи к металлической. ). При всей искусственности такого подхода в этом есть что-то полезное. Рис. 3 демонстрирует распределение плотности электронного заряда в кристаллах с различным типом связи и переход от ковалентной связи к металлической.
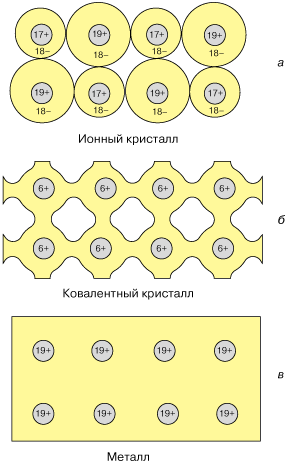 | Рис. 3. Схематическое двухмерное изображение распределения электронного заряда в твердых телах: а - ионный кристалл, б - ковалентный кристалл, в - металл.
|
С самого начала своего развития теория металлов основывалась на простейшей модели, в которой электроны проводимости рассматривались как идеальный газ свободных частиц. Первые работы, в которых электронный газ в металле описывался с помощью классической статистики, не смогли объяснить все свойства металлов. Однако положенная в их основу модель была настолько удачной, что дополнение ее принципом Паули привело к удивительно хорошему объяснению экспериментально наблюдаемых свойств, таких, как электропроводность, теплопроводность металлов и др. Успех модели свободных электронов был парадоксальным, поскольку в металле электроны движутся в поле сильного ионного кристаллического (периодического) потенциала. Учет периодичности действующего на электроны в кристалле ионного потенциала позволил показать, что их энергетический спектр имеет зонную структуру, а энергия электронов является функцией импульса (точнее, квазиимпульса - этим подчеркивается, что электрон движется в кристалле). Рассмотрим подробнее эти представления.
Назад | Вперед
Посмотреть комментарии[1]
|

