П.В. Кузьмин (Костромская Государственная Сельскохозяйственная
Академия)
Издательство КГСХА, 2002 г.
| Содержание |
Найдем период колебаний. Если упругое свойство симметрично относительно
среднего положения системы, то время движения маятника от крайнего положения
к среднему равно четверти периода колебаний. Тогда
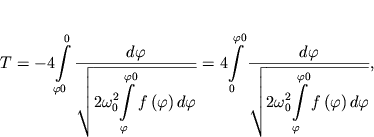 | (a) |
где крайнее положение (максимальное отклонение) имеет координату 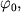 а среднее координату равную нулю. а среднее координату равную нулю.
Рассмотрим частный случай
Пусть имеется система, представляющая собой физический маятник.
Физический маятник - твердое тело, колеблющееся в вертикальной плоскости под действием силы
тяжести.
Момент, действующий на маятник, является некоторой функцией угла поворота.
тогда
Введем обозначение 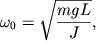 получим получим
Т.е. в данном случае 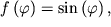 тогда, применив выражение (a), получим тогда, применив выражение (a), получим
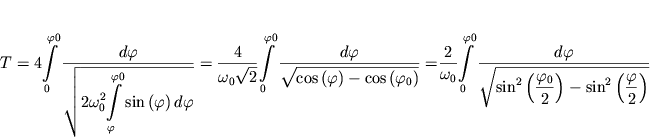 | (b) |
Вводя обозначение 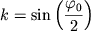 и
новую переменную и
новую переменную 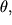 так что так что
Получим
Из выражения (b) получаем окончательно для периода колебаний
![$ T = {\displaystyle \frac{{\displaystyle 4}}{{\displaystyle \omega _{0} }}}{\displaystyle \int\limits_{0}^{{{\displaystyle \pi } / {\displaystyle 2}}} {{\displaystyle \frac{{\displaystyle d\theta }}{{\displaystyle \sqrt {{\displaystyle \left[ {\displaystyle 1 - k^{2}\sin ^{2}\theta } \right]}} }}}} } $](http://images.nature.web.ru/nature/2002/06/10/0001187014/tex/formula199.gif) | (c) |
Выражение (c) - это полный эллиптический интеграл Лежандра первого рода, численное решение которого можно взять из таблиц. [С.П. Тимошенко, 1959]
Однако, поскольку 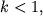 решение можно получить в виде бесконечного ряда
[Г. Корн, Т. Корн, 1984]. решение можно получить в виде бесконечного ряда
[Г. Корн, Т. Корн, 1984].
Тогда выражение (c) можно преобразовать к виду [М.М. Гернет, 1987]
![$ T = {\displaystyle \frac{{\displaystyle 2\pi }}{{\displaystyle \omega _{0} }}}{\displaystyle \left[ {\displaystyle 1 + \left( {{\displaystyle \frac{{\displaystyle 1}}{{\displaystyle 2}}}} \right)^{2}\sin ^{2}\left( {{\displaystyle \frac{{\displaystyle \varphi _{0} }}{{\displaystyle 2}}}} \right) + \left( {{\displaystyle \frac{{\displaystyle 1}}{{\displaystyle 2}}} \cdot {\displaystyle \frac{{\displaystyle 3}}{{\displaystyle 4}}}} \right)^{2}\sin ^{4}\left( {{\displaystyle \frac{{\displaystyle \varphi _{0} }}{{\displaystyle 2}}}} \right) + \ldots } \right]}. $](http://images.nature.web.ru/nature/2002/06/10/0001187014/tex/formula202.gif) | (d) |
Если 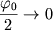 (мало), тогда можно считать, что (мало), тогда можно считать, что
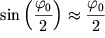 и выражение (d) принимает вид и выражение (d) принимает вид
Если выражением 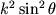 можно пренебречь, то при предельном
переходе получим можно пренебречь, то при предельном
переходе получим
формулу для периода колебаний физического маятника с линейной
восстанавливающей силой.
Из истории физики известно, что независимость периода колебаний от амплитуды
при малых колебаниях, была замечена Галилеем. Т.е. только малые колебания
являются гармоническими. Это связано с тем, что только при малых отклонениях
от положения равновесия можно считать, что возвращающая сила пропорциональна
смещению. Поэтому период колебаний (или частота) не будут зависеть от
амплитуды колебаний, а будут зависеть только от свойств системы.
- Свободные колебания возникают под действием внутренних сил в системе, которая была выведена из положения равновесия.
- Если восстанавливающая сила пропорциональна смещению системы из положения равновесия, то колебания будут гармоническими. Частота и период не зависят от амплитуды колебаний.
- Частота свободных колебаний зависит только от свойств системы.
- Амплитуда свободных колебаний зависит от начальных условий.
- Если в системе отсутствуют силы сопротивления, то колебания будут незатухающими, т.е. будут продолжаться сколь угодно долго.
- Если в системе действуют силы сопротивления, то колебания будут затухающими, т.е. не будут продолжаться сколь угодно долго. Их амплитуда будет уменьшаться с течением времени.
- Вид зависимости амплитуды от времени зависит от вида функции сопротивления. Подобная зависимость впервые была отмечена Ньютоном. Если
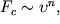 тогда тогда 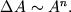 Т.е., если сила сопротивления пропорциональна скорости (первой производной координаты по времени), то амплитуда колебаний будет убывать по экспоненциальному закону. Т.е., если сила сопротивления пропорциональна скорости (первой производной координаты по времени), то амплитуда колебаний будет убывать по экспоненциальному закону.
- Коэффициент затухания зависит от свойств системы.
- Если восстанавливающая сила не является линейной функцией смещения системы из положения равновесия, то колебания будут негармоническими. Частота и период будут зависеть от амплитуды колебаний.
(На примере пружинного маятника.)
Пусть на пружинный маятник действует периодическая внешняя сила (см. рис.
2.1.1).
Тогда уравнение движения груза
в скалярной форме можно привести к виду
или
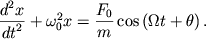 | (11) |
Выражение (11) - это дифференциальное уравнение вынужденных гармонических незатухающих колебаний.
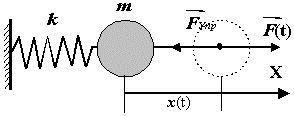 | | Рис. 2.1.1 |
Решение уравнения (11) будем искать в виде:
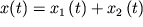 | (12) |
Где 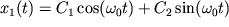 -
решение, соответствующее собственным гармоническим незатухающим колебаниям, -
решение, соответствующее собственным гармоническим незатухающим колебаниям,
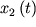 - решение, соответствующее вынужденным гармоническим колебаниям. - решение, соответствующее вынужденным гармоническим колебаниям.
Возможны три случая:
1. Случай отсутствия резонанса (условие 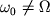 ) )
В этом случае частное решение следует искать в виде 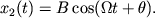 Подставим решение в уравнение (11) и определим Подставим решение в уравнение (11) и определим 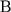 . .
Т.к. косинус переменного аргумента равен нулю не для всех значений времени,
то равенство выполняется только тогда, когда
Отсюда
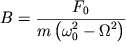 | (13) |
Назад| Вперед
Написать комментарий
| 
