Научная Сеть >> Колебания. Краткий конспект лекций.

Наука >> Физика >> Общая физика >> Колебания и волны >> Электрические колебания | Курсы лекций

Написать комментарий

Добавить новое сообщение

См. также

Б.А. Бахметев дипломат, политик, мыслитель

Колебания. Краткий конспект лекций.

П.В. Кузьмин (Костромская Государственная Сельскохозяйственная Академия)
Издательство КГСХА, 2002 г.

Содержание

Амплитуда силы тока имеет максимальное (резонансное) значение равное

$I_{0\max } = {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle 2L\beta }}}\quad или \quad I_{0\max } = {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle R}}}.$

Подставим в выражение (61) значения 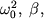$\omega _{0}^{2} ,\; \beta ,$ тогда получим

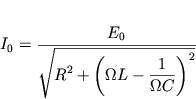$I_{0} = {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle \sqrt {\displaystyle R^{2} + \left( {\displaystyle \Omega L - {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \Omega C}}}} \right)^{2}} }}}$

(62)

Выражение (62) закон Ома для цепи переменного тока. Значения силы тока и ЭДС в законе можно брать мгновенные, амплитудные или действующие.

Дополнительно найдем

${\displaystyle \rm tg}\varepsilon = - {\displaystyle \frac{{\displaystyle R}}{{\displaystyle \Omega L - {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \Omega C}}}}}}.$

Выражение (60) для силы тока можно преобразовать к виду:

$I\left( {\displaystyle t} \right) = {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle \sqrt {\displaystyle R^{2} + \left( {\displaystyle \Omega L - {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \Omega C}}}} \right)^{2}} }}}\cos \left( {\displaystyle \Omega t + \theta + \varepsilon + {\displaystyle \frac{{\displaystyle \pi }}{{\displaystyle 2}}}} \right),$

где обозначим 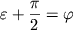$\varepsilon + {\displaystyle \frac{{\displaystyle \pi }}{{\displaystyle 2}}} = \varphi$ - сдвиг фаз между током и приложенным внешним напряжением (ЭДС) (см. рис. 7.2.2)

$tg\varphi = - {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle tg\varepsilon }}} = {\displaystyle \frac{{\displaystyle \Omega L - {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \Omega C}}}}}{{\displaystyle R}}}$

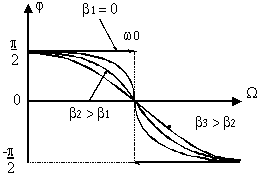Рис. 7.2.2

Напряжение на катушке при вынужденных колебаниях в электрическом контуре:

$U_{L} \left( {\displaystyle t} \right) = L{\displaystyle \frac{{\displaystyle \Omega E_{0} }}{{\displaystyle \sqrt {\displaystyle R^{2} + \left( {\displaystyle \Omega L - {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \Omega C}}}} \right)^{2}} }}}\cos \left( {\displaystyle \Omega t + \varphi + {\displaystyle \frac{{\displaystyle \pi }}{{\displaystyle 2}}}} \right)$

или

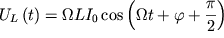$U_{L} \left( {\displaystyle t} \right) = \Omega LI_{0} \cos \left( {\displaystyle \Omega t + \varphi + {\displaystyle \frac{{\displaystyle \pi }}{{\displaystyle 2}}}} \right)$

(63)

Векторная диаграмма 2 показывает "взаимное расположение" напряжений на различных элементах контура в начальный момент времени. Для простоты начальная фаза приложенного напряжения выбрана равной нулю. Поскольку контур последовательный, т.е. все элементы соединены последовательно, то сила тока, текущего через каждый его элемент, будет одинакова. Напряжения же будут различны.

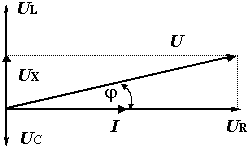Векторная диаграмма 2

При помощи векторной диаграммы удобно условно отражать напряжения и силы тока на различных элементах контура с учетом фазовых соотношений.

Векторная диаграмма 3 показывает, какие будут происходить изменения с течением времени. Вращение векторов происходит против часовой стрелки с циклической частотой 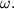$\omega .$ Текущая фаза колебаний будет изменяться линейно с течением времени. Силу тока и напряжение на каждом элементе контура в любой момент времени можно найти спроецировав соответствующий вектор на ось Re. Фазовые соотношения между напряжениями на различных элементах контура в процессе колебаний не изменяются.

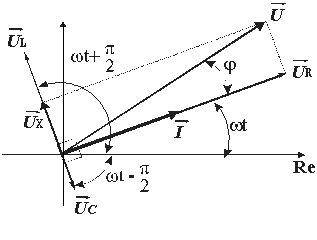Векторная диаграмма 3

7.3. Сопротивления в цепи переменного тока

Рассмотрим последовательный колебательный контур. Воспользуемся законом Ома для цепи переменного тока (62)

Рассмотрим участки, состоящие только из индуктивности или только емкости. Тогда для индуктивного участка (сравнить с (63))

$I_{0} = {\displaystyle \frac{{\displaystyle U_{L0} }}{{\displaystyle \Omega L}}}.$

Аналогично для емкостного участка

$I_{0} = U_{C0} \Omega C.$

Сравнивая полученные выражения с законом Ома для участка цепи постоянного тока, можно заключить, что катушка в цепи переменного тока обладает дополнительным сопротивлением, которое связано с наличием индуктивности, и равным 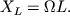$X_{L} = \Omega L.$ Это сопротивление называется индуктивным сопротивлением.

Конденсатор также обладает дополнительным сопротивлением, связанным с процессами зарядки-разрядки и равным 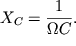$X_{C} = {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \Omega C}}}.$ Это так называемое емкостное сопротивление.

Общее название индуктивного и емкостного сопротивления - реактивное сопротивление. Реактивное сопротивление не приводит к потерям энергии, оно создает сдвиг фаз между током и напряжением в цепи переменного тока, что является нежелательным.

Окончательно можно сделать вывод, что в цепи переменного тока "сосуществуют" два типа сопротивления. Активное сопротивление, которое приводит к выделению тепла на элементах цепи. Реактивное сопротивление, состоящее из индуктивного и емкостного, которое приводит к сдвигу фаз между током и напряжением.

7.4. Замечания о резонансе в электрической цепи

1. Последовательный колебательный контур.

Контур, в котором все элементы подключены последовательно, называется последовательным колебательным контуром. В пунктах (7.1) и (7.2) был рассмотрен именно такой контур.

В последовательном колебательном контуре: резонанс явление резкого увеличения силы тока в контуре при приближении частоты внешнего воздействия к собственной частоте колебаний контура.

Амплитуда силы тока при резонансе

$I_{0\max } = {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle R}}}$

Индуктивное сопротивление контура при резонансе равно нулю!

Резонанс в последовательном контуре носит название резонанса напряжений.

(см. векторную диаграмму 4.)

Векторная диаграмма 4

Это связано с тем, что напряжения в таком контуре играют ключевую роль. На различных участках контура они различны по величине. Поскольку напряжение на индуктивности и напряжение на емкости колеблются в противофазе, максимальная сила тока достигается, когда они равны по модулю. Учитывая, что сила тока одинакова на всех элементах контура, от напряжений можно перейти к сопротивлениям, т.е. 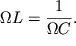$\Omega L = {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \Omega C}}}.$

Таким образом:

Максимальная сила тока при резонансе определяется только активным сопротивлением контура.
Резонанс происходит на частоте собственных незатухающих колебаний.
Суммарное реактивное сопротивление контура равно нулю. Сила тока и напряжение, подаваемое на контур, колеблются в одинаковой фазе (разность фаз равна нулю).
В состоянии резонанса можно передать от источника к приемнику максимальную при данном напряжении активную мощность.

2. Параллельный колебательный контур.

Контур, в котором электроемкость, индуктивность и активное сопротивление включены параллельно друг другу, называется параллельным колебательным контуром. (Схема 5.)

Схема 5

Воспользуемся первым правилом Кирхгофа, получим с учетом разности фаз токов (см. векторную диаграмму 5.)

$I = \sqrt {\displaystyle I_{R}^{2} + \left( {\displaystyle I_{C} - I_{L} } \right)^{2}} = U\sqrt {{\displaystyle \frac{{\displaystyle 1}}{{\displaystyle R^{2}}}} + \left( {\displaystyle \Omega C - {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \Omega L}}}} \right)^{2}} .$

Величина равная

$Z = {\displaystyle \frac{{\displaystyle U}}{{\displaystyle I}}} = {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \sqrt {{\displaystyle \frac{{\displaystyle 1}}{{\displaystyle R^{2}}}} + \left( {\displaystyle \Omega C - {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \Omega L}}}} \right)^{2}} }}}$

называется полным сопротивлением параллельного контура.

Векторная диаграмма 5

Сдвиг фаз можно найти из векторной диаграммы

$\cos \varphi = {\displaystyle \frac{{\displaystyle I_{R} }}{{\displaystyle I}}} = {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle R\sqrt {{\displaystyle \frac{{\displaystyle 1}}{{\displaystyle R^{2}}}} + \left( {\displaystyle \Omega C - {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \Omega L}}}} \right)^{2}} }}}$

При приближении частоты внешней ЭДС к собственной частоте колебаний контура наблюдается резкое уменьшение силы тока, потребляемого от источника. Это явление называется резонанс токов.

Это связано с тем, что сила тока, текущего через индуктивность и сила тока, текущего через емкость колеблются в противофазе, минимальная сила тока в неразветвленной части цепи достигается, когда они равны по модулю. (см. рис.7.4.1) Учитывая, что напряжение одинаково на всех элементах контура, от силы тока можно перейти к проводимостям (величинам обратным сопротивлениям), т.е. 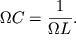$\Omega C = {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \Omega L}}}.$

Рис. 7.4.1

В таком контуре энергия, потребляемая при резонансе от источника питания, идет на компенсацию тепловых потерь при прохождении тока через активное сопротивление.

Таким образом:

Минимальная сила тока в неразветвленной части цепи при резонансе определяется только активным сопротивлением контура.
Резонанс происходит на частоте собственных незатухающих колебаний.
Суммарный "реактивный" ток контура равен нулю. "Реактивный" ток - это ток через индуктивность + ток через емкость. Сила тока и напряжение,
подаваемое на контур, колеблются в одинаковой фазе (разность фаз равна нулю).
В состоянии резонанса можно передать от источника к приемнику максимальную при данном напряжении активную мощность. [О.Ф. Кабардин и др., 1979]

Назад| Вперед

П.В.Кузьмин

Написать комментарий