Научная Сеть >> Механика твердого тела. Лекции.

Наука >> Физика >> Общая физика >> Механика | Курсы лекций

Посмотреть комментарии[3]

Добавить новое сообщение

См. также

Механика сплошных сред: Лекция 1

Красота физики в уродливом мире.

Антон Дмитриевич Билимович

Колебания и волны: Лекция 1

Виктор Антонович САДОВНИЧИЙ "Математическое образование. Настоящее и будущее.": Московский университет

Механика твердого тела. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 1997 г.

Содержание

Необходимость введения тензорных величин связана с различного рода анизотропией свойств физических макроскопических объектов. Тензор связывает две векторные величины, которые пропорциональны друг другу по модулю, но в силу анизотропии свойств объекта не совпадают друг с другом по направлению. В случае L и 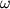$\omega$ решающую роль играет "анизотропия" формы тела (отсутствие определенной симметрии относительно осей xyz). В других случаях это может быть анизотропия, например, электрических или магнитных свойств вещества. Так, векторы поляризации вещества Р и напряженности электрического поля Е связаны тензором поляризуемости $\hat {\displaystyle \alpha }$ : $\bf P} = \varepsilon _{0} \hat {\displaystyle \alpha }{\displaystyle \bf E} (\varepsilon _{0$ - электрическая постоянная). Это означает, что в силу анизотропии электрических свойств вещество поляризуется "не по полю", то есть "не по полю" смещаются положительные и отрицательные заряды в молекулах вещества. Примерами других, в общем случае тензорных величин являются диэлектрическая проницаемость и магнитная проницаемость вещества. Важную роль в механике играют тензоры деформаций и напряжений. С этими и другими тензорными величинами вы познакомитесь при изучении соответствующих разделов курса общей физики.

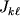Замечание. Если ${\displaystyle \bf r}_{i} , \omega$ и L в выражении (2.3) проектировать на оси лабораторной системы XYZ, то компоненты тензора $J_{k\ell }$ оказались бы зависящими от времени. Такой подход в принципе возможен; он, в частности, используется в Берклеевском курсе физики [Ч. Киттель и др., 1983].

Главные оси инерции.

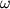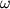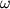Возникает вопрос: возможен ли для произвольного твердого тела случай, когда векторы L и $\omega$ совпадают? Оказывается, что для всякого тела и любой точки О имеются по крайней мере три взаимно перпендикулярных направления $\omega$ (или, другими словами, три взаимно перпендикулярных оси вращения), для которых направления L и $\omega$ совпадают. Такие оси называются главными осями инерции тела.

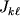Если оси Ox, Oy и Oz совместить с главными осями инерции тела, то матрица $J_{k\ell }$ будет иметь диагональный вид:

$\hat {\displaystyle J}_{0} = \left( {\displaystyle {\displaystyle \begin{array}{*{20}c} {\displaystyle J_{xx} } \hfill & {\displaystyle 0} \hfill & {\displaystyle 0} \hfill \\ {\displaystyle 0} \hfill & {\displaystyle J{\displaystyle }_{yy}} \hfill & {\displaystyle 0} \hfill \\ {\displaystyle 0} \hfill & {\displaystyle 0} \hfill & {\displaystyle J_{zz} } \hfill \\ \end{array} }} \right).$

(2.15)

Величины $J_{xx} \equiv J_{x} , J_{yy} \equiv J_{y} , J_{zz} \equiv J_{z}$ в этом случае называются главными моментами инерции тела. При этом

$L_{x} = J_{x} \omega _{x} ; L_{y} = J_{y} \omega _{y} ; L_{z} = J_{z} \omega _{z} ,$

(2.16)

то есть, действительно, если вектор 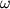$\omega$ направлен вдоль одной из главных осей инерции тела, то вектор L будет направлен точно так же (рис. 2.6).

Рис. 2.6.

Расположение главных осей инерции в теле и значения соответствующих главных моментов инерции зависят от выбора точки О. Если О совпадает с центром масс, то главные оси называются главными центральными осями тела. Если главные оси инерции тела известны, то значения главных моментов инерции вычисляются из геометрии масс. Например:

$J_{x} = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }\left( {\displaystyle r_{i}^{2} - x_{i}^{2} } \right) = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }\left( {\displaystyle y_{i}^{2} + z_{i}^{2} } \right) = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }\rho _{i}^{2} .$

(2.17)

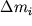Здесь $\rho _{i}$ - расстояние элементарной массы $\Delta m_{i}$ от главной оси Ox.

Как же определить главные оси инерции для выбранной точки О твердого тела? Если оси Ox, Oy и Oz проведены в теле произвольно, то в общем случае они не совпадают с главными осями инерции. Такого совпадения можно добиться путем некоторого поворота исходной системы координат относительно твердого тела. В новых координатах матрица 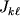$J_{k\ell }$ становится диагональной.

Во многих случаях главные оси инерции удается легко определить из соображений симметрии. На рис. 2.7-2.10 изображены главные оси инерции для различных точек тел, обладающих определенной симметрией: цилиндра (рис. 2.7), прямоугольного параллелепипеда (рис. 2.8), куба (рис. 2.9) и шара (рис. 2.10). Легко сообразить, что во всех этих случаях $J_{xy} = J_{xz} = J_{yx} = J_{yz} = J_{zx} = J_{zy} = 0.$ Например, в случае прямоугольного параллелепипеда (рис. 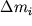2.8) $J_{xy} = - {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }x_{i} y_{i} = 0,$ так как для всякой массы $\Delta m_{i}$ с данными значениями $x_{i} , y_{i} , z_{i}$ найдется симметрично расположенная масса $\Delta {\displaystyle m}'_{i}$ с теми же значениями $x_{i}$ и $z_{i}$ , но с противоположным значением $y_{i}.$


Рис. 2.7.	Рис. 2.8.

Рис. 2.9.	Рис. 2.10.

В заключение этого раздела рассмотрим пример нахождения главных осей инерции для плоской прямоугольной пластинки со сторонами 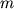$a$ и $b,$ масса которой $m$ (рис. 2.11).

Рис. 2.11.

Ясно, что одна из главных осей инерции для точки О (ось Oz) перпендикулярна плоскости пластинки; на рис. 2.11 она не показана. Оси Ox и Oy, направленные вдоль сторон пластинки, не являются главными. Действительно, в этом случае

$J_{xx} = \int {\displaystyle y^{2}} dm = {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle ab}}}{\displaystyle \int\limits_{0}^{a} {\displaystyle dx{\displaystyle \int\limits_{0}^{b} {\displaystyle y^{2}} }} }dy = m{\displaystyle \frac{\displaystyle {\displaystyle b^{2}}}{\displaystyle {\displaystyle 3}}};$

(2.18)

$J_{yy} = \int {\displaystyle x^{2}} dm = {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle ab}}}{\displaystyle \int\limits_{0}^{b} {\displaystyle dy{\displaystyle \int\limits_{0}^{a} {\displaystyle x^{2}} }} }dx = m{\displaystyle \frac{\displaystyle {\displaystyle a^{2}}}{\displaystyle {\displaystyle 3}}};$

(2.19)

$J_{xy} = - \int {\displaystyle xy} dm = - {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle ab}}}{\displaystyle \int\limits_{0}^{a} {\displaystyle xdx{\displaystyle \int\limits_{0}^{b} {\displaystyle y} }} }dy = - m{\displaystyle \frac{\displaystyle {\displaystyle ab}}{\displaystyle {\displaystyle 3}}} < 0$

(2.20)

Допустим, что оси Ox' и Oy', повернутые на угол 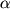$\alpha$ относительно осей Ox и Oy - главные оси инерции для точки О. Соответствующее преобразование координат имеет вид:

$\left\{\displaystyle {\displaystyle \begin{array}{l} {\displaystyle x = {\displaystyle x}'\cos \alpha + {\displaystyle y}'\sin \alpha ;} \\ {\displaystyle y = - {\displaystyle x}'\sin \alpha + {\displaystyle y}'\cos \alpha } \\ \end{array}} \right.}. \quad \begin{array}{l} (1.21) \\ (1.22) \\ \end{array$

Тогда будем иметь

$J_{xx} = \int {\displaystyle y^{2}} dm = \int {\displaystyle \left( {\displaystyle - {\displaystyle x}'\sin \alpha + {\displaystyle y}'\cos \alpha } \right)} ^{2}dm = J_{{\displaystyle y}'} \sin ^{2}\alpha + J_{{\displaystyle x}'} \cos ^{2}\alpha .$

(2.23)

Здесь учтено, что для главных осей Ox' и Oy' $\int {\displaystyle {\displaystyle x}'{\displaystyle y}'dm = 0.}$

Аналогично

$J_{yy} = \int {\displaystyle x^{2}} dm = \int {\displaystyle \left( {\displaystyle {\displaystyle x}'\cos \alpha + {\displaystyle y}'\sin \alpha } \right)} ^{2}dm = J_{{\displaystyle y}'} \cos ^{2}\alpha + J_{{\displaystyle x}'} \sin ^{2}\alpha .$

(2.24)

$J_{xy} = - \int {\displaystyle xy} dm = - \int {\displaystyle \left( {\displaystyle - {\displaystyle x}'\cos \alpha + {\displaystyle y}'\sin \alpha } \right)\left( {\displaystyle - {\displaystyle x}'\sin \alpha + {\displaystyle y}'\cos \alpha } \right){\displaystyle \kern 1pt} } dm = - {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\sin 2\alpha (J_{{\displaystyle x}'} - J_{{\displaystyle y}'} ).$

(2.25)

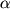Подставляя в (2.23 - 2.25) значения $J_{xx} , J_{yy}$ и $J_{xy}$ из (2.18 - 2.20), получим систему трех уравнений для нахождения $J_{{\displaystyle x}'} , J_{{\displaystyle y}'}$ и $\alpha$ :

$\left\{\displaystyle {\displaystyle \begin{array}{l} {\displaystyle J_{{\displaystyle y}'} \sin ^{2}\alpha + J_{{\displaystyle x}'} \cos ^{2}\alpha = m{\displaystyle \frac{\displaystyle {\displaystyle b^{2}}}{\displaystyle {\displaystyle 3}}};} \\ {\displaystyle J_{{\displaystyle y}'} \cos ^{2}\alpha + J_{{\displaystyle x}'} \sin ^{2}\alpha = m{\displaystyle \frac{\displaystyle {\displaystyle a^{2}}}{\displaystyle {\displaystyle 3}}};} \\ {\displaystyle \left( {\displaystyle J_{{\displaystyle x}'} - J_{{\displaystyle y}'} } \right)\sin 2\alpha = m{\displaystyle \frac{\displaystyle {\displaystyle ab}}{\displaystyle {\displaystyle 3}}};} \\ \end{array}} \right.} \quad \begin{array}{l} (2.26) \\ (2.27) \\ (2.28) \\ \end{array$

Из этой системы, в частности, легко получить, что

${\displaystyle \rm tg}2\alpha = {\displaystyle \frac{\displaystyle {\displaystyle 3}}{\displaystyle {\displaystyle 2}}} \cdot {\displaystyle \frac{\displaystyle {\displaystyle ab}}{\displaystyle {\displaystyle \left( {\displaystyle b^{2} - a^{2}} \right)}}}.$

(2.29)

Для сравнения: если $\alpha _{0}$ - угол между осью Oy и диагональю прямоугольной пластинки, то

${\displaystyle \rm tg}2\alpha _{0} = {\displaystyle \frac{\displaystyle {\displaystyle 2ab}}{\displaystyle {\displaystyle b^{2} - a^{2}}}},$

(2.30)

то есть $\alpha \lt \alpha _{0} .$ Это означает, что главная ось инерции Oy' не проходит через центр пластинки. И только в случае квадрата, когда $a = b, \alpha = {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 4}}},$ главная ось инерции Oy' будет направлена по диагонали квадрата. Этот пример наглядно показывает, что если главные оси инерции - нецентральные, то ни одна из них в принципе может и не проходить через центр масс тела.

Назад| Вперед

Физический факультет МГУ

Посмотреть комментарии[3]