10. В этой главе мы
обратимся к рассмотрению квантового аналога исходной динамической системы. Его
состояния эволюционируют по интервалу  . В соответствии с общими принципами квантовой механики,
дифференциальное уравнение эволюции динамических состояний частицы имеет вид: . В соответствии с общими принципами квантовой механики,
дифференциальное уравнение эволюции динамических состояний частицы имеет вид:
где 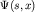 есть скалярная волновая функция частицы в
координатном представлении. Ковариантность полученного уравнения относительно
преобразований Лоренца очевидна, ибо оператор Лапласа-Бельтрами есть скалярная волновая функция частицы в
координатном представлении. Ковариантность полученного уравнения относительно
преобразований Лоренца очевидна, ибо оператор Лапласа-Бельтрами 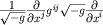 является релятивистски инвариантным оператором, а
волновая функция является релятивистски инвариантным оператором, а
волновая функция 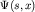 есть скаляр относительно преобразований Лоренца. По
существу уравнение (IV.3) - это уравнение Шредингера, соответствующее движению
скалярной частицы в геодезических полях. Выражение для действия в этом случае
имеет вид: есть скаляр относительно преобразований Лоренца. По
существу уравнение (IV.3) - это уравнение Шредингера, соответствующее движению
скалярной частицы в геодезических полях. Выражение для действия в этом случае
имеет вид: 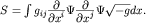
20. Запишем уравнение
(IV.1) для  -стационарного случая,
разделив переменные в волновой функции. Для этого сделаем подстановку -стационарного случая,
разделив переменные в волновой функции. Для этого сделаем подстановку
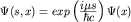 . По существу это значит, что рассматриваемая система
находится в состоянии, характеризуемом определенным значением массы. Уравнение
(IV.3) сведется к задаче на собственные функции гамильтониана (IV.1): . По существу это значит, что рассматриваемая система
находится в состоянии, характеризуемом определенным значением массы. Уравнение
(IV.3) сведется к задаче на собственные функции гамильтониана (IV.1):
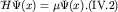
Данное уравнение есть не что иное, как уравнение Клейна-Гордона-Фока в случае произвольной метрики 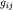 , описывающее динамическое состояние скалярной частицы в
отсутствие других взаимодействий, помимо гравитационного. , описывающее динамическое состояние скалярной частицы в
отсутствие других взаимодействий, помимо гравитационного.
Рассмотрим, например, это уравнение в псевдоевклидовой метрике,
когда метрический тензор 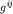 имеет диагональный вид с сигнатурой имеет диагональный вид с сигнатурой
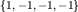 а интервал определяется
формулой а интервал определяется
формулой
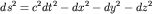 . Тогда уравнение (IV.2) примет вид . Тогда уравнение (IV.2) примет вид
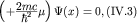
где 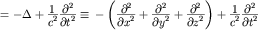 - оператор д'Аламбера. Сравнивая полученное уравнение с известным уравнением
Клейна-Гордона-Фока в декартовой системе координат, видим, что они совпадают
при - оператор д'Аламбера. Сравнивая полученное уравнение с известным уравнением
Клейна-Гордона-Фока в декартовой системе координат, видим, что они совпадают
при 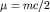 . Таким образом, . Таким образом,  с точностью до множителя с точностью до множителя
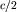 следует трактовать как массовую
характеристику исходной динамической системы (частицы). Этот множитель связан с
собственным значением оператора Лапласа-Бельтрами
следует трактовать как массовую
характеристику исходной динамической системы (частицы). Этот множитель связан с
собственным значением оператора Лапласа-Бельтрами 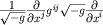 , на
основе которого построен квантовый гамильтониан (III.1). Свойства оператора
Лапласа - Бельтрами хорошо изучены; в частности, известен его спектр, благодаря
чему можно сделать некоторые заключения относительно физических свойств
описываемой системы и геометрии пространства. , на
основе которого построен квантовый гамильтониан (III.1). Свойства оператора
Лапласа - Бельтрами хорошо изучены; в частности, известен его спектр, благодаря
чему можно сделать некоторые заключения относительно физических свойств
описываемой системы и геометрии пространства.
В статье [9] при некоторых дополнительных предположениях
математического характера показано, что в эллиптическом случае у оператора
Лапласа - Бельтрами на римановом многообразии существует серия асимптотических
собственных функций и соответствующих им собственных значений вида
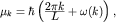
где 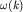 - некий характеристический показатель, а
- некий характеристический показатель, а  - длина контура некоторой геодезической. По существу это
указывает на существенную зависимость между массой частицы и степенью ее
локализации в пространственно-временном континууме. - длина контура некоторой геодезической. По существу это
указывает на существенную зависимость между массой частицы и степенью ее
локализации в пространственно-временном континууме.
Как нетрудно убедиться, в случае "слабой" метрики (пункт
II.20) уравнение Клейна-Гордона-Фока имеет следующий вид:
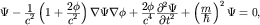
где через 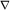 обозначен вектор частных производных по пространственным координатам
обозначен вектор частных производных по пространственным координатам 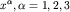 , а , а 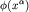 - скалярный гравитационный потенциал. - скалярный гравитационный потенциал.
30. Некоторые авторы
(см., например, [5]) пишут уравнение Клейна-Гордона-Фока для случая
произвольной метрики в виде:
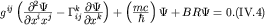
где  - некоторый
постоянный коэффициент, - некоторый
постоянный коэффициент, 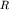 - кривизна
пространства, - кривизна
пространства, 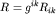 . .
Воспользовавшись тождеством 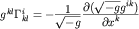 ,
нетрудно показать, что при предложенной трактовке собственного значения ,
нетрудно показать, что при предложенной трактовке собственного значения  уравнения (IV.2) и (IV.4) совпадают с точностью до члена уравнения (IV.2) и (IV.4) совпадают с точностью до члена
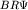 ,
вводимого обычно "из соображений конформной инвариантности" уравнения
(IV.4).
Коэффициент ,
вводимого обычно "из соображений конформной инвариантности" уравнения
(IV.4).
Коэффициент  различен при различных способах получения уравнения (IV.4) и требованиях к нему [5]. Вообще говоря, слагаемое различен при различных способах получения уравнения (IV.4) и требованиях к нему [5]. Вообще говоря, слагаемое 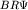 можно получить и в нашем подходе, использовав для построения квантового гамильтониана
не просто оператор Лапласа-Бельтрами, а с аддитивно добавленным оператором умножения на можно получить и в нашем подходе, использовав для построения квантового гамильтониана
не просто оператор Лапласа-Бельтрами, а с аддитивно добавленным оператором умножения на 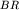 , так что , так что
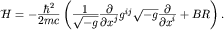
Эрмитовость оператора 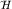 при
этом сохранится, так как скалярная кривизна при
этом сохранится, так как скалярная кривизна 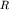 есть инвариант [2]. При выборе коэффициента есть инвариант [2]. При выборе коэффициента
 надо исходить опять-таки из требований, предъявляемых к свойствам получаемого уравнения. Если пространство
имеет постоянную кривизну, набор собственных функций квантового гамильтониана после предлагаемой модификации не изменится. надо исходить опять-таки из требований, предъявляемых к свойствам получаемого уравнения. Если пространство
имеет постоянную кривизну, набор собственных функций квантового гамильтониана после предлагаемой модификации не изменится.
Назад
Написать комментарий
| 
