Научная Сеть >> Уравнение Власова-Эйнштейна и его квантование

Наука >> Физика >> Теоретическая физика >> Квантовая механика | Дипломные работы

Амосов С.А. (Московский физико-технический институт, факультет управления и прикладной математики)
Научный руководитель: д.ф.-м.н. Веденяпин В.В.
Москва, 1997

Содержание

Глава II. Гамильтонов формализм для уравнений Власова-Эйнштейна.

Некоторые частные случаи.

1⁰. Перейдем в системе уравнений (I.4) к гамильтоновым переменным. Гамильтониан частицы запишем в виде:
$H=\frac{\displaystyle{1}}{\displaystyle{2mc}}g^{ij}p_ip_j\equiv\frac{\displaystyle{1}}{\displaystyle{2mc}}g_{ij}p^ip^j, \mbox{(II.1)}$

где $c$ - cкорость света, $m$ - массовая характеристика частицы, $p_i$ канонически сопряженные импульсы для обобщенных координат . Как и прежде, индекс $0$ соответствует временным компонентам, а индексы $1,2$ и $3$ - пространственным компонентам 4-векторов. Связь 4-импульса с 4-скоростью выражается известной формулой:
$p_i=mcv_i.\mbox{II.2}$

Заметим, что роль времени в классической механике здесь играет интервал $s$ , а само время рассматривается как одна из координат. Уравнения Гамильтона будут иметь вид:

что соответствует уравнениям геодезических (I.1). Точка вверху означает здесь полную производную по интервалу $s$ .

Восстановим на многообразии $M$ пуассонову структуру. Скобку Пуассона для двух функций с аргументами из фазового пространства $(x,p)$ определим следующим образом:
$g^{\alpha\alpha}\equiv{}-1\mbox{(II.4)}$

(напомним, что по повторяющимся на разных уровнях индексам производится суммирование). Тогда верхнее уравнение системы Власова-Эйнштейна (I.4) в гамильтоновых переменных примет вид:

$\frac{\displaystyle{\partial{}F}}{\displaystyle{\partial{}s}}+\frac{\displaystyle{1}}{\displaystyle{mc}}p^i\frac{\displaystyle{\partial{}F}}{\displaystyle{\partial{}x^i}}-\frac{\displaystyle{1}}{\displaystyle{mc}}\gamma^i_{kl}p^kp^l\frac{\displaystyle{\partial{}F}}{\displaystyle{\partial{}p^i}}=0, \mbox{(II.5)}$

или $\frac{\displaystyle{\partial{}F}}{\displaystyle{\partial{}s}}+\{F,H\}=0$ - в форме Лиувилля. Нижнее уравнение системы (I.4) (уравнение Эйнштейна) формально не изменится, но в тензоре энергии-импульса зависимость от компонент 4-скорости $v^i$ следует в соответствии с (II.2) рассматривать как зависимость от импульсов $p^i$ :
$R^{ik}-g^{ik}R=\gamma\int{}p^ip^kF\sqrt{-g}dp.$

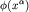2⁰. В качестве примера рассмотрим уравнения Власова-Эйнштейна для случая слабой метрики [2,3]. Тогда $g_{00}=1+\frac{\displaystyle{2\phi{}(x^{\alpha})}}{\displaystyle{c^2}},\alpha=1,2,3; g_{11}=g_{22}=g_{33}=-1$ , то есть
$ds^2=(c^2+2\phi{}(\vec{}r))dt^2-d\vec{}r^2.\mbox{(II.6)}$

Здесь $\phi{}(x^{\alpha})$ - скалярный потенциал, зависящий от пространственных координат. Заметим, что в силу симметричности метрического тензора фазовые переменные с одинаковыми верхним и нижним индексами тождественны. В рассматриваемом приближении отличны от нуля следующие символы Кристоффеля:
$\gamma^{\alpha}_{00}=\frac{\displaystyle{1}}{\displaystyle{c^2}}\frac{\displaystyle{\partial{}\phi}}{\displaystyle{\partial{}x^{\alpha}}}, \alpha=1,2,3.$

При этом R_0^0=\frac{\displaystyle{1}}{\displaystyle{c^2}}\Delta\phi, где $\Delta$ - оператор Лапласа (дивергенция градиента) по пространственным координатам, и, как показано в [2,3], уравнение Эйнштейна переходит в уравнение Пуассона для скалярного потенциала:
$\Delta\phi=4\pi{}G\rho$

где $\rho$ - массовая плотность, а G - некоторая константа, связанная с гравитационной постоянной соотношением $G=\frac{\displaystyle{\gamma{}c^4}}{\displaystyle{8\pi}}$ . Решение уравнения Пуассона для произвольного распределения масс приведено в [2].

Перейдем к $s$ -стационарному случаю в уравнении Власова-Эйнштейна, воспользовавшись описанной в пункте I.2⁰ подстановкой с учетом вида метрики (II.6). При этом произведем пространственно-временное расщепление основных переменных, приняв $x^i=(ct,\vec{}r), p^i=\left(\frac{\displaystyle{E}}{\displaystyle{c}},\vec{}p\right).$ . Интегралом уравнений геодезических для рассматриваемого случая будет $\left(1+\frac{\displaystyle{2\phi{}(x)}}{\displaystyle{c^2}}\right)\frac{\displaystyle{E^2}}{\displaystyle{m^2c^4}}-\frac{\displaystyle{1}}{\displaystyle{m^2c^2}}p_{\alpha}p^{\alpha}$ . Верхнее уравнение системы (I.5) теперь можно записать как
$\frac{\displaystyle{E}}{\displaystyle{c^2}}\frac{\displaystyle{\partial{}f}}{\displaystyle{\partial{}t}}+p_{\alpha}\frac{\displaystyle{\partial{}f}}{\displaystyle{\partial{}x^{\alpha}}}+\left(\frac{\displaystyle{E}}{\displaystyle{c^2}}\right)g^{\alpha\alpha}\frac{\displaystyle{\partial{}\phi}}{\displaystyle{\partial{}x^{\alpha}}}\frac{\displaystyle{\partial{}f}}{\displaystyle{\partial{}p^{\alpha}}}=0 \mbox{(II.7)}$

Здесь $\alpha=1,2,3$ , $f\equiv{}f(t,\vec{}r,E,\vec{}p)$ . В последнем слагаемом все $g^{\alpha\alpha}\equiv{}-1$ , и они оставлены здесь в таком виде лишь для того, чтобы не нарушать правило суммирования по повторяющимся индексам.

В результате $s$ -стационарная система уравнений Власова-Эйнштейна (I.5) в случае слабой метрики переходит в систему Власова-Пуассона:

Отдельный интерес представляет также следующий факт: множитель, стоящий при $\nabla_xf$ и в обычном уравнении Власова трактуемый как кинематическая скорость, в рассматриваемом случае есть $c^2\vec{}p/E$ , то есть скорость групповая для частиц с импульсом $\vec{}p$ и энергией $E$ , а множитель при $\nabla_pf$ , играющий роль силы, равен $-E\nabla_x\phi/c^2$ . Нетрудно убедиться в том, что эти две величины совпадают с обычными скоростью и силой при $E\cong{}mc^2$ . Это приближение вполне согласуется с условием, обеспечивающим "слабость" метрики, а именно - малостью характерных скоростей частиц рассматриваемой системы по сравнению со скоростью света. В терминах физической кинетики вышеизложенное означает, что в бесстолкновительном случае гравитация как тип взаимодействия доминирует, если облако частиц велико, а их температура низка.

Некоторые частные решения системы (II.8) приведены в работе [8] Меллота и Сентреллы, где они используются для численного моделирования крупномасштабной структуры Вселенной.

3⁰. Приведем теперь вид уравнения Власова-Эйнштейна для метрики Шварцшильда [2,3] в сферически симметричном случае. Тогда $x^i=\left(ct,r,\theta,\phi\right),p^i=\left(\frac{\displaystyle{E}}{\displaystyle{c}},p_r,p_{\theta},p_{\phi}\right)$ , а выражение для интервала выглядит следующим образом:
$ds^2=\left(1-\frac{\displaystyle{r_g}}{\displaystyle{r}}\right)c^2dt^2-r^2\left(sin^2\theta{}d\phi^2+d\theta^2\right)-\frac{\displaystyle{1}}{\displaystyle{1-\frac{\displaystyle{r_g}}{\displaystyle{r}}}}dr^2. \mbox{(II.9)}$

Здесь $r_g=\frac{\displaystyle{}2Gm}{\displaystyle{}c^2}$ - так называемый гравитационный радиус тела. Это решение уравнения Эйнштейна определяет гравитационное поле в пустоте, создаваемое любым центрально-симметричным распределением масс. Оно справедливо, в частности, и для центрально-симметричных движений [2]. Напишем уравнение Власова для этого случая. Отличным от нуля символом Кристоффеля является $\gamma^r_{tt}=\frac{\displaystyle{r_g}}{\displaystyle{2r^2}}\left(1-\frac{\displaystyle{r_g}}{\displaystyle{r}}\right)$ , и уравнение Власова имеет вид:
$\frac{\displaystyle{E}}{\displaystyle{c}}\frac{\displaystyle{\partial{}f}}{\displaystyle{\partial{}t}}+p_r\frac{\displaystyle{\partial{}f}}{\displaystyle{\partial{}r}}-\frac{\displaystyle{r_g}}{\displaystyle{2r^2}}\left(1-\frac{\displaystyle{r_g}}{\displaystyle{r}}\right)\left(\frac{\displaystyle{E}}{\displaystyle{c}}\right)\frac{\displaystyle{\partial{}f}}{\displaystyle{\partial{}p_r}}=0 \mbox{(II.10)}$

Назад | Вперед

Кинетическая теория

Написать комментарий