Векторное пространство
(линейное пространство) - множество элементов, называемых
векторами, для
которых определены операции сложения и умножения
на число. Простейший, но важный пример - совокупность векторов a, b,
c, ... обычного 3-мерного пространства. Каждый такой вектор - направленный
отрезок, задаваемый тремя числами: 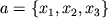 ;
числа
;
числа
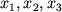 называются координатами вектора.
При умножении
вектора на вещественное число
называются координатами вектора.
При умножении
вектора на вещественное число 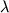 соответствующий отрезок, сохраняя направление, растягивается в
соответствующий отрезок, сохраняя направление, растягивается в 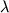 раз:
раз:
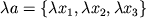 . Сумма
двух векторов находится по
правилу параллелограмма; если
. Сумма
двух векторов находится по
правилу параллелограмма; если 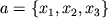 и
и 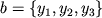 то
то 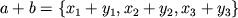 .
Паре
векторов a и b сопоставляют также скалярное
произведение
.
Паре
векторов a и b сопоставляют также скалярное
произведение 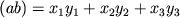 (см. Векторная алгебра).
Непосредственным обобщением З-мерного пространства является n-мерное
евклидово пространство. Его элементы
- упорядоченные
наборы вещественных чисел,
Например,
(см. Векторная алгебра).
Непосредственным обобщением З-мерного пространства является n-мерное
евклидово пространство. Его элементы
- упорядоченные
наборы вещественных чисел,
Например, 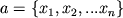 ,
, 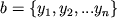 .
Сложение
и умножение векторов на число определены формулами
.
Сложение
и умножение векторов на число определены формулами
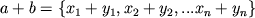 ,
, 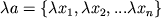 , а скалярное произведение - формулой
, а скалярное произведение - формулой 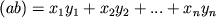 Примером комплексного бесконечномерного векторного пространства
может служить совокупность
Примером комплексного бесконечномерного векторного пространства
может служить совокупность 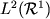 комплексных функций
f,
заданных на всей оси
комплексных функций
f,
заданных на всей оси 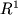 и квадратично суммируемых (то есть
имеющих конечный интеграл
и квадратично суммируемых (то есть
имеющих конечный интеграл 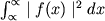 ).
Многие
классы
функций, например, полиномы заданного порядка,
функции непрерывные, дифференцируемые,
интегрируемые,
аналитические
и тому подобные, также образуют бесконечномерные векторные пространства.
).
Многие
классы
функций, например, полиномы заданного порядка,
функции непрерывные, дифференцируемые,
интегрируемые,
аналитические
и тому подобные, также образуют бесконечномерные векторные пространства.
В каждом векторном пространстве, помимо операций сложения и умножения на
число, обычно имеются те или иные дополнительные операции и структуры (например,
определено
скалярное
произведение). Если же не уточняют природы элементов векторного пространства
и не предполагают в нем никаких дополнительных свойств, то векторное пространство
называют
абстрактным. Абстрактное векторное
пространство
L задают с помощью следующих аксиом:
- любой паре элементов х и у из L сопоставлен единственный элемент z, называемый их суммой z=x+y и принадлежащий L;
- для любого числа
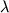 и любого элемента x из L определен
элемент z, который называется их произведением
и любого элемента x из L определен
элемент z, который называется их произведением 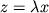 и
принадлежащий L;
и
принадлежащий L;
- операции сложения и умножения на число являются ассоциативными и дистрибутивными.
Сложение допускает обратную операцию, то есть для любых
х и
у из
L
существует единственный элемент
w из
L такой, что
x+w=y.
Кроме того, имеют место формулы
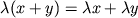
. Если
все
числа
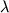
вещественны
(комплексны), говорят о вещественном
(комплексном)
векторном пространстве; множество чисел
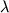
называют
полем скаляров
L. Понятие векторного пространства можно ввести и для произвольного
поля, например, поля кватернионов.
Если 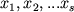 - элементы векторного пространства L,
то выражение
вида
- элементы векторного пространства L,
то выражение
вида 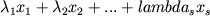 называется
их линейной комбинацией; совокупность всех линейных
комбинаций
элементов подмножества S из L
называют линейной
оболочкой S. Векторы
называется
их линейной комбинацией; совокупность всех линейных
комбинаций
элементов подмножества S из L
называют линейной
оболочкой S. Векторы 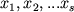 из L
называют линейно независимыми, если условие
из L
называют линейно независимыми, если условие
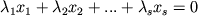 (
(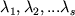 - любые элементы
поля скаляров) может выполняться только при
- любые элементы
поля скаляров) может выполняться только при 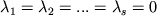 .
Бесконечная система векторов называется линейно независимой, если любая
ее
конечная
часть
является линейно независимой. Множество элементов
.
Бесконечная система векторов называется линейно независимой, если любая
ее
конечная
часть
является линейно независимой. Множество элементов
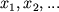 подмножества S из L называется системой образующих S, если любой вектор х
из
S
можно
представить в виде линейной комбинации этих элементов. Линейно независимая
система образующих S называется базисом S, если
разложение
любого
элемента S по
этой системе единственно. Базис, элементы которого каким-либо
образом параметризованы, называется системой
координат в S. Базис векторного пространства всегда существует, хотя и
не
определяется однозначно. Если базис состоит из конечного числа n элементов,
то векторное пространство называется n-мерным
(конечномерным); если
базис - бесконечное множество, то
векторное пространство называется бесконечномерным.
Выделяют также счетномерные векторные
пространства,
у которых имеется счетный базис.
подмножества S из L называется системой образующих S, если любой вектор х
из
S
можно
представить в виде линейной комбинации этих элементов. Линейно независимая
система образующих S называется базисом S, если
разложение
любого
элемента S по
этой системе единственно. Базис, элементы которого каким-либо
образом параметризованы, называется системой
координат в S. Базис векторного пространства всегда существует, хотя и
не
определяется однозначно. Если базис состоит из конечного числа n элементов,
то векторное пространство называется n-мерным
(конечномерным); если
базис - бесконечное множество, то
векторное пространство называется бесконечномерным.
Выделяют также счетномерные векторные
пространства,
у которых имеется счетный базис.
Подмножества векторного пространства L, замкнутые относительно его
операций, называются подпространствами L.
По любому подпространству S можно построить новое векторное пространство
L/S, называемое фактор-пространством
L по S:
каждый его элемент есть множество векторов из L,
различающихся между собой на элемент из S. Размерность L/S
называется коразмерностью подпространства
S
в
L;
если размерности L и S равны соответственно n и k,
то коразмерность S в L равна n-k. Если
J - произвольное множество индексов i и Si
- семейство подпространств L, то совокупность всех векторов,
принадлежащих каждому из Si, есть подпространство,
называется пересечением указанных
подпространств
и обозначаемое 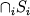 . Для конечного семейства подпространств
S1, ..., Ss совокупность всех векторов, представимых
в виде
. Для конечного семейства подпространств
S1, ..., Ss совокупность всех векторов, представимых
в виде
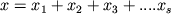 , xi из Si, , xi из Si, |
(*) |
есть подпространство, называемое
суммой
S1, ..., Ss и обозначаемое
S1+ ... +Ss.
Если для любого элемента суммы
S1+ ... +Ss представление в виде (*) единственно,
эта
сумма называется прямой и обозначается
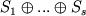
. Сумма
подпространств является прямой тогда и только тогда,
когда пересечение этих подпространств состоит только
из
нулевого вектора.
Размерность
суммы подпространств равна сумме размерностей этих подпространств
минус размерность их пересечения. Векторное пространство
L1
и
L2 называют
изоморфным и, если существует
взаимно однозначное соответствие между их элементами, согласованное с операциями
в них;
L1
и
L2 изоморфны тогда и
только тогда, когда они имеют одинаковую размерность.
Конкретные примеры векторного пространства можно найти в математическом аппарате
практически любого раздела физики.
Конечномерными вещественными векторными пространствами являются, например,
трехмерное физическое пространство 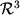 (без учета кривизны),
конфигурационное пространство
(без учета кривизны),
конфигурационное пространство 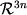 и фазовое пространство
и фазовое пространство
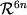 системы n классических точечных частиц.
К числу бесконечномерных комплексных векторных пространств принадлежат гильбертовы
пространства,
конкретные и абстрактные, составляющие основу математического аппарата квантовой
физики. Простейший пример гильбертова пространств уже упоминавшееся пространство
системы n классических точечных частиц.
К числу бесконечномерных комплексных векторных пространств принадлежат гильбертовы
пространства,
конкретные и абстрактные, составляющие основу математического аппарата квантовой
физики. Простейший пример гильбертова пространств уже упоминавшееся пространство
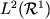 .
Основные физические
примеры - пространства векторов состояний различных систем микрочастиц, изучаемых
в квантовой механике, квантовой статистической
физике
и квантовой теории
поля. Находят применение и такие векторные поля, у которых поле
скаляров не совпадает со множеством вещественных
или комплексных чисел: так, гильбертово пространство
над полем кватернионов используется и одной из формулировок
квантовой механики, а гильбертово пространство над полем октонионов
- в одной из формулировок квантовой хромодинамики.
В современных теориях
суперсимметрии интенсивно применяются так называемые градуированные
векторные поля, то есть линейные пространства вместе
с
их фиксированным разложением в прямую бесконечную сумму подпространств.
.
Основные физические
примеры - пространства векторов состояний различных систем микрочастиц, изучаемых
в квантовой механике, квантовой статистической
физике
и квантовой теории
поля. Находят применение и такие векторные поля, у которых поле
скаляров не совпадает со множеством вещественных
или комплексных чисел: так, гильбертово пространство
над полем кватернионов используется и одной из формулировок
квантовой механики, а гильбертово пространство над полем октонионов
- в одной из формулировок квантовой хромодинамики.
В современных теориях
суперсимметрии интенсивно применяются так называемые градуированные
векторные поля, то есть линейные пространства вместе
с
их фиксированным разложением в прямую бесконечную сумму подпространств.

