Вектор состояния
(амплитуда состояния; символ
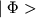 или
или 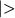 , предложен П.
А. М. Дираком) - основное
понятие квантовой механики, математический объект, задание
которого в определенный момент времени полностью определяет
состояние квантовомеханической системы и, при известных взаимодействиях,
ее дальнейшую эволюцию. Тот
факт, что объект, описывающий состояние в квантовой
механике, в математическом отношении должен представлять
собой вектор, вытекает из основного принципа квантовой
механики - принципа суперпозиции состояний (см.
Суперпозиции
принцип). Из этого принципа следует также, что совокупность векторов состояния
какой-либо физической системы образует комплексное векторное пространство,
которое может
быть конечномерным или бесконечномерным
в зависимости от того, содержит ли оно конечное или бесконечное число линейно независимых
векторов состояний. Исходя из определения скалярного
произведения вектора состояния, можно каждому вектору
, предложен П.
А. М. Дираком) - основное
понятие квантовой механики, математический объект, задание
которого в определенный момент времени полностью определяет
состояние квантовомеханической системы и, при известных взаимодействиях,
ее дальнейшую эволюцию. Тот
факт, что объект, описывающий состояние в квантовой
механике, в математическом отношении должен представлять
собой вектор, вытекает из основного принципа квантовой
механики - принципа суперпозиции состояний (см.
Суперпозиции
принцип). Из этого принципа следует также, что совокупность векторов состояния
какой-либо физической системы образует комплексное векторное пространство,
которое может
быть конечномерным или бесконечномерным
в зависимости от того, содержит ли оно конечное или бесконечное число линейно независимых
векторов состояний. Исходя из определения скалярного
произведения вектора состояния, можно каждому вектору 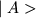 этого пространства взаимно однозначно сопоставить сопряженный
(дуальный) ему вектор
этого пространства взаимно однозначно сопоставить сопряженный
(дуальный) ему вектор 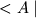 , связанный с
, связанный с 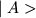 следующими соотношениями: если
следующими соотношениями: если
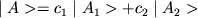 , где c1,
c2 - произвольные комплексные числа, то
, где c1,
c2 - произвольные комплексные числа, то 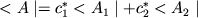 (
( означает комплексное
сопряжение). По терминологии, предложенной
Дираком, вектор
означает комплексное
сопряжение). По терминологии, предложенной
Дираком, вектор 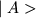 называется "кет",
а сопряженный ему
вектор
называется "кет",
а сопряженный ему
вектор 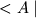 - "бра", что отвечает
разбиению английского слова bracket (скобка) на две части. Если координаты
вектора "кет"
- "бра", что отвечает
разбиению английского слова bracket (скобка) на две части. Если координаты
вектора "кет" 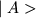 в каком-либо базисе
представлять в виде столбца
в каком-либо базисе
представлять в виде столбца 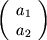 ,
то координаты вектора "бра"
,
то координаты вектора "бра" 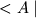 в сопряженном базисе
могут быть представлены строкой из комплексно-сопряженных чисел: (
в сопряженном базисе
могут быть представлены строкой из комплексно-сопряженных чисел: (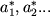 ),
а скалярное
произведение двух векторов состояния
),
а скалярное
произведение двух векторов состояния 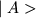 и
и 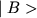 , обозначаемое
, обозначаемое
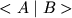 (причем
(причем 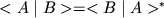 ), получается по правилам матричного умножения
(см.
Матрица) путем умножения строки, отвечающей
), получается по правилам матричного умножения
(см.
Матрица) путем умножения строки, отвечающей 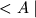 , на столбец, отвечающий
, на столбец, отвечающий 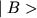 . Вследствие взаимно
однозначного соответствия между векторами "кет" и "бра" любое состояние
динамической системы может быть описано с помощью как
вектора состояния "кет", так и вектора состояния "бра".
. Вследствие взаимно
однозначного соответствия между векторами "кет" и "бра" любое состояние
динамической системы может быть описано с помощью как
вектора состояния "кет", так и вектора состояния "бра".
Скалярное произведение вектора состояния 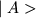 само на себя
называется нормой
само на себя
называется нормой 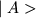 . Оно представляет собой
обобщение
квадрата длины обычного вектора. В квантовой механике
постулируется, что вектора состояния динамической системы обладают
конечной
неотрицательной нормой:
. Оно представляет собой
обобщение
квадрата длины обычного вектора. В квантовой механике
постулируется, что вектора состояния динамической системы обладают
конечной
неотрицательной нормой: 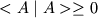 . (Для
векторов состояния, отвечающих "нефизическим" переменным, это
требование может быть ослаблено; см. Индефинитная
метрика.)
. (Для
векторов состояния, отвечающих "нефизическим" переменным, это
требование может быть ослаблено; см. Индефинитная
метрика.)
В пространстве вектор состояния имеет смысл понятие ортогональности,
которое является обобщением соответствующего понятия для обычных векторов:
два
вектора состояния 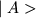 и
и 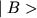 называются
ортогональными друг другу, если
называются
ортогональными друг другу, если
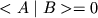 .
.
Для задания произвольного вектора состояния динамической системы
используется в качестве ортогонального нормированного (ортонормированного)
базиса совокупность векторов состояния,
отвечающих полному набору измеряемых физических величин
для данной системы, т. е. если величины F, G, ..., H
составляют полный набор, а 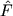 ,
, 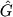 , ...,
, ...,
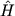 - соответствующие им эрмитовы операторы,
то в
качестве
базиса
используются собственные векторы состояний.
- соответствующие им эрмитовы операторы,
то в
качестве
базиса
используются собственные векторы состояний.
где
F,
G, ...,
H(обозначим их набор для краткости
одной буквой
n) -
собственные значения операторов
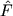
,
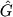
, ...,
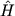
. Если
n образуют дискретный
спектр, то соответствующие им собственные векторы состояния
могут быть нормированы на единицу:
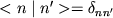
|
(2) |
здесь
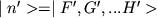
,
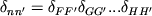
-
символ Кронекера:
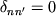
, если
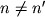
и
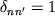
,
если
n=
n' (т. е. если
F=F', G=G', ... H=H').
Произвольный вектор состояния динамической системы
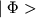
может быть
представлен в виде разложения:
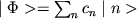 , ,
|
(3) |
где
cn - координаты вектора состояния
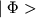
в базисе
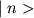
- представляют собой функцию переменных
n,
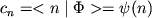
Функция 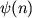 называется волновой функцией
в представлении
величин n. Квадрат модуля волновой функции
называется волновой функцией
в представлении
величин n. Квадрат модуля волновой функции 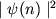 ,
согласно статистической интерпретации квантовой механики, равен вероятности
того, что для системы, находящейся в состоянии, описываемом вектором
состояния
,
согласно статистической интерпретации квантовой механики, равен вероятности
того, что для системы, находящейся в состоянии, описываемом вектором
состояния 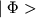 , набор
определяющих состояние величин равен n. Таким образом, волновая функция
представляет собой амплитуду вероятности. Поскольку
задание
волновой функции
полностью определяет вектор состояния
, набор
определяющих состояние величин равен n. Таким образом, волновая функция
представляет собой амплитуду вероятности. Поскольку
задание
волновой функции
полностью определяет вектор состояния 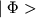 динамической
системы,
можно вычислить вероятности возможных значений
Ki любой другой физической величины K, не входящей
в полный набор (n). Для этого вектор состояния
динамической
системы,
можно вычислить вероятности возможных значений
Ki любой другой физической величины K, не входящей
в полный набор (n). Для этого вектор состояния 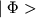 должен
быть
разложен
но векторам состояния, отвечающим другому полному набору
величин, включающему величину К (см. Представлений
теория).
должен
быть
разложен
но векторам состояния, отвечающим другому полному набору
величин, включающему величину К (см. Представлений
теория).
Если собственные значения n (или некоторые из них) образуют сплошной
спектр, суммирование в (3)
заменяется интегрированием по соответствующим величинам, а условие (2) нормировки
собственных векторов состояния на
единицу заменяется условием нормировки на дельта-функцию:
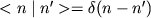
|
(2') |
Квадрат модуля волновой функции в этом случае равен
плотности вероятности данного состояния.
Вероятность
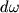
того, что для системы с векторами состояния
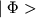
величины (
n) будут обнаружены в интервалах
n+dn, равна:
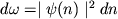
Формально условие (2') противоречит постулату квантовой
механики, требующему существования конечной
нормы вектора состояния. Это связано с тем, что вектора состояния, отвечающий
определенному значению физической величины, имеющей непрерывный спектр, является
математической идеализацией. В действительности любая физическая величина
F,
принимающая
непрерывные значения, может быть определена только
с некоторой
степенью точности 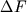
,
зависящей от
разрешения прибора. Поэтому "физические" вектора
состояния,
отвечающие
заданному (среднему) значению измеренной величины
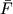
, представляют
собой по существу
волновой пакет:
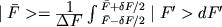
|
(4) |
[В более общем случае суперпозиция вектора состояния
(4) может
содержать коэффициенты
c(F'), плавно меняющиеся
в интервале
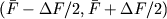
]. При условии
нормировки (2'):
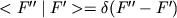
норма вектора состояния
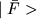
конечна:
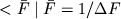
при любом конечном
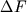
Таким образом,
"физические" вектора состояния (4) удовлетворяют требованию существования
конечной нормы. Однако в математическом отношении
использование их представляет ряд неудобств. Поэтому
в аппарате квантовой механики, как правило, используют
"монохроматические"
векторы состояния с условием нормировки
(2'), имея в виду, что из них всегда можно составить
"физические" векторы состояния с конечной нормой.
Для динамической системы, состоящей из N частиц, полным набором измеряемых
величин может служить совокупность пространственных координат всех частиц
(x1, y1, z1, ..., xN, yN,
zN) вместе с величинами, определяющими внутренние степени
свободы частиц (например, спинами) 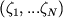 . Координаты вектора состояния в этом базисе
. Координаты вектора состояния в этом базисе
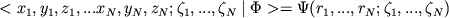
называется волновой функцией в конфигурационном представлении.
Условие существования конечной нормы вектора состояния:
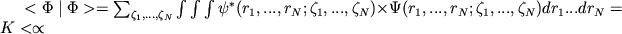
означает, что вектора состояний принадлежат гильбертову
пространству. Использование в математическом аппарате квантовой
механики собственных векторов состояний с бесконечной нормой (2')
для величин, имеющих непрерывный спектр, требует
формального расширения пространства Гильберта
путем включения в него также вектора состояния с бесконечной нормой при условии,
что
волновые пакеты (4), составленные из суперпозиции таких векторов состояний,
обладают конечной
нормой.
В квантовой теории поля вектор состояния часто задается
в чисел
заполнения представлении. Вектор состояния системы частиц с импульсами
p1, ..., pN и другими квантовыми
числами 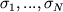 :
:
получается (с точностью до нормирующего множителя) в результате действия операторов
рождения частиц (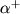 ) на вектор состояния вакуума
) на вектор состояния вакуума
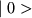 :
:
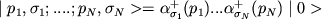
В случае, когда число частиц в системе может изменяться (т. е. в результате
взаимодействий происходит
рождение или уничтожение частиц), для задания вектора состояния
используется также Фока представление (в котором число
частиц и системе не фиксировано).

