В любой колебательной системе с одной
степенью свободы смещение 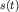 и скорость и скорость  меняются со
временем. Состояние системы в каждый момент времени можно характеризовать
двумя значениями меняются со
временем. Состояние системы в каждый момент времени можно характеризовать
двумя значениями  и и  и на плоскости этих переменных это состояние
однозначно определяется положением изображающей точки P с координатами и на плоскости этих переменных это состояние
однозначно определяется положением изображающей точки P с координатами  и и
 . С течением времени изображающая точка P будет перемещаться по кривой,
которую называют фазовой траекторией движения (рис. 1.10). . С течением времени изображающая точка P будет перемещаться по кривой,
которую называют фазовой траекторией движения (рис. 1.10).
 | | Рис. 1.10. |
Плоскость переменных  и и  называется фазовой плоскостью. Семейство фазовых
траекторий образует фазовый портрет колебательной системы. Анализ фазового
портрета дает хотя и не полную, но обширную информацию о колебательной
системе. К построению такого портрета прибегают тогда, когда не удается
решить аналитически уравнение, описывающее сложные колебания. В первую
очередь это относится к нелинейным колебаниям, анализ которых затруднен
из-за отсутствия точных решений нелинейных уравнений. называется фазовой плоскостью. Семейство фазовых
траекторий образует фазовый портрет колебательной системы. Анализ фазового
портрета дает хотя и не полную, но обширную информацию о колебательной
системе. К построению такого портрета прибегают тогда, когда не удается
решить аналитически уравнение, описывающее сложные колебания. В первую
очередь это относится к нелинейным колебаниям, анализ которых затруднен
из-за отсутствия точных решений нелинейных уравнений.
Вначале проиллюстрируем сказанное на примере простейших гармонических
колебаний вида  Поскольку скорость
Поскольку скорость  опережает смещение по фазе на
опережает смещение по фазе на  то фазовая траектория будет
эллипсом. Точка P будет двигаться по эллиптической траектории по часовой
стрелке (при то фазовая траектория будет
эллипсом. Точка P будет двигаться по эллиптической траектории по часовой
стрелке (при  смещение смещение  увеличивается, а при увеличивается, а при  - уменьшается (рис.
1.11)). - уменьшается (рис.
1.11)).
 | | Рис. 1.11. |
Параметры эллипса определяются энергией, запасенной гармоническим
осциллятором. Потенциальная энергия пружинного маятника пропорциональна
квадрату смещения:
 | (1.24) |
Кинетическая энергия пропорциональна квадрату скорости:
 | (1.25) |
Если принять во внимание равенство  то легко видеть,
что взаимопревращения одного вида энергии в другой за период происходят
дважды. При этом полная энергия системы остается постоянной: то легко видеть,
что взаимопревращения одного вида энергии в другой за период происходят
дважды. При этом полная энергия системы остается постоянной:
 | (1.26) |
Равенство (1.26) как раз и является уравнением эллипса, которое можно
переписать в более удобном виде:
 | (1.27) |
Фазовый портрет гармонического осциллятора представляет собой семейство
эллипсов, каждому из которых соответствует энергия  запасенная
осциллятором. Положение равновесия в точке 0 на фазовой плоскости является
особой точкой и называется особой точкой типа "центр". запасенная
осциллятором. Положение равновесия в точке 0 на фазовой плоскости является
особой точкой и называется особой точкой типа "центр".
С увеличением энергии  возрастают амплитуды колебаний смещения возрастают амплитуды колебаний смещения
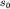 и скорости и скорости  Колебания, как правило, перестают
быть гармоническими, а фазовые траектории - эллипсами. Колебания, как правило, перестают
быть гармоническими, а фазовые траектории - эллипсами.
 | | Рис. 1.12. |
Проанализируем на фазовой плоскости колебания математического маятника при
произвольных углах  отклонения от положения равновесия. При этом
будем считать, что точечная масса отклонения от положения равновесия. При этом
будем считать, что точечная масса 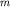 прикреплена не к нити, а к жесткому
невесомому стержню длины прикреплена не к нити, а к жесткому
невесомому стержню длины  Первое из уравнений (1.2) запишем в виде Первое из уравнений (1.2) запишем в виде
 | (1.28) |
Это нелинейное уравнение не имеет точного аналитического решения, поэтому
позднее мы приведем его приближенное решение. Однако многие закономерности
таких колебаний можно проанализировать с использованием фазового портрета на
плоскости  С этой
целью уравнение (1.28) надо преобразовать к такому виду, чтобы в нем
остались только эти переменные, а время было бы исключено. Для этого угловое
ускорение в левой части (1.28) преобразуем к виду: С этой
целью уравнение (1.28) надо преобразовать к такому виду, чтобы в нем
остались только эти переменные, а время было бы исключено. Для этого угловое
ускорение в левой части (1.28) преобразуем к виду:
 | (1.29) |
Подставляя (1.29) в (1.28), получим
 | (1.30) |
Уравнение (1.30) отражает тот факт, что приращение кинетической энергии
маятника равно убыли его потенциальной энергии в поле силы тяжести.
Интегрируя (1.30), получим
 | (1.31) |
Если принять, что потенциальная энергия маятника в положении равновесия
равна нулю, то константа выражается через запасенную маятником энергию
 ( ( - угловая скорость маятника в положении равновесия): - угловая скорость маятника в положении равновесия):
 | (1.32) |
Уравнение фазовой траектории (1.31) окончательно запишется в виде:
 | (1.33) |
При этом потенциальная и кинетическая энергии задаются выражениями
 | (1.34) |
Используя (1.33), построим фазовый портрет системы (рис. 1.13).
 | | Рис. 1.13. |
Отчетливо видны два типа фазовых траекторий, соответствующие двум типам
движения. Замкнутые траектории, окружающие особые точки типа "центр" с
координатами  ( ( - целое число),
соответствуют колебаниям маятника относительно устойчивого нижнего положения
равновесия. Такие колебания имеют место, если энергия системы - целое число),
соответствуют колебаниям маятника относительно устойчивого нижнего положения
равновесия. Такие колебания имеют место, если энергия системы  (см. рис. 1.13). При этом, если (см. рис. 1.13). При этом, если  то колебания будут гармоническими, а фазовые траектории - эллипсами. Если то колебания будут гармоническими, а фазовые траектории - эллипсами. Если  то колебания будут негармоническими.
При увеличении энергии, а, значит, и амплитуды колебаний осциллятора, их
период будет возрастать, поскольку возвращающая сила в уравнении (1.28)
меньше, чем в случае гармонического осциллятора. то колебания будут негармоническими.
При увеличении энергии, а, значит, и амплитуды колебаний осциллятора, их
период будет возрастать, поскольку возвращающая сила в уравнении (1.28)
меньше, чем в случае гармонического осциллятора.
Верхнему положению равновесия с координатами  соответствуют особые точки типа "седло".
Фазовые кривые, проходящие через "седла", соответствуют энергии соответствуют особые точки типа "седло".
Фазовые кривые, проходящие через "седла", соответствуют энергии  и называются сепаратрисами. и называются сепаратрисами.
Если, наконец,  то получаются незамкнутые (убегающие)
траектории, соответствующие вращательному движению маятника. то получаются незамкнутые (убегающие)
траектории, соответствующие вращательному движению маятника.
Таким образом, сепаратрисы разделяют фазовую плоскость на две области:
область замкнутых траекторий и область траекторий, приходящих из
бесконечности и уходящих в бесконечность.
Отметим, что для негармонических колебаний нельзя употреблять термин
"круговая частота", поскольку, как будет показано ниже, такие колебания
являются, как правило, суперпозицией гармонических колебаний с различными
частотами. Период же является по-прежнему одной из главных характеристик
колебаний. Фазовый портрет не позволяет определить, как быстро движется
точка Р по траектории. Однако период нелинейных колебаний математического
маятника можно получить на основе приближенного решения уравнения (1.28).
Назад| Вперед
Посмотреть комментарии[2]
| 
