Если положение системы может быть описано одним единственным параметром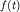 ,
зависящим от времени, то такая система имеет одну степень свободы. Примерами
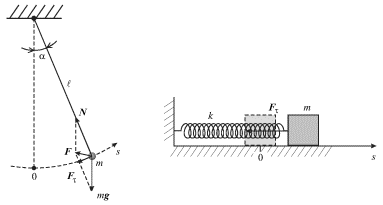
таких систем являются хорошо известные из школьного курса математический и
пружинный маятники, изображенные на рис. 1.1, если первый из них движется в
одной плоскости, а второй - по прямой. ,
зависящим от времени, то такая система имеет одну степень свободы. Примерами
таких систем являются хорошо известные из школьного курса математический и
пружинный маятники, изображенные на рис. 1.1, если первый из них движется в
одной плоскости, а второй - по прямой.
 | | Рис. 1.1. |
Для математического маятника 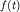 может характеризовать либо угловое
смещение может характеризовать либо угловое
смещение 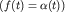 , либо линейное смещение вдоль траектории , либо линейное смещение вдоль траектории
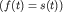 точечной массы точечной массы 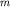 от положения равновесия, а для пружинного
маятника от положения равновесия, а для пружинного
маятника 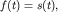 где где 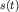 - смещение массы m от ее равновесного
положения, изображенного пунктиром. - смещение массы m от ее равновесного
положения, изображенного пунктиром.
Движение таких и подобных им систем можно описать на основе второго закона
Ньютона:
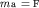 | (1.1) |
Если пренебречь вначале силами сопротивления (в дальнейшем мы учтем их
действие), то на массу 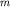 математического маятника будет действовать
результирующая сила математического маятника будет действовать
результирующая сила 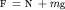 ( ( - сила натяжения нити), направленная,
вообще говоря, под углом к траектории, а на массу - сила натяжения нити), направленная,
вообще говоря, под углом к траектории, а на массу 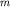 пружинного маятника,
лежащего на гладкой горизонтальной поверхности, - горизонтальная сила пружинного маятника,
лежащего на гладкой горизонтальной поверхности, - горизонтальная сила
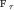 , являющаяся функцией смещения , являющаяся функцией смещения  от положения равновесия. от положения равновесия.
Так как смещение 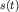 в случае математического маятника определяется
тангенциальным ускорением, то уравнение (1.1) для обоих маятников запишется
в виде в случае математического маятника определяется
тангенциальным ускорением, то уравнение (1.1) для обоих маятников запишется
в виде
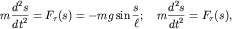 | (1.2) |
где  - длина нити. - длина нити.
В первом уравнении использована проекция 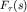 результирующей силы результирующей силы
 на направление скорости в виде на направление скорости в виде 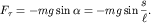
В рассматриваемых примерах возвращающая сила 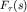 является,
вообще говоря, нелинейной функцией смещения является,
вообще говоря, нелинейной функцией смещения  . Поэтому точное решение
уравнений (1.2), которые являются нелинейными, получить не удается. Далее мы
рассмотрим некоторые примеры таких нелинейных колебаний. . Поэтому точное решение
уравнений (1.2), которые являются нелинейными, получить не удается. Далее мы
рассмотрим некоторые примеры таких нелинейных колебаний.
Здесь же мы будем считать смещения малыми по сравнению с длиной нити или
длиной недеформированной пружины. При таких предположениях возвращающая сила
пропорциональна смещению:
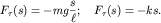 | (1.3) |
Выражение слева записано при учете условия 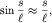 а справа - с использованием закона Гука,
справедливого при малых деформациях пружины с жесткостью а справа - с использованием закона Гука,
справедливого при малых деформациях пружины с жесткостью 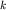 . .
С учетом (1.3) уравнения (1.2) примут одинаковый вид:
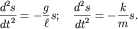 | (1.4) |
Различаются лишь коэффициенты в правых частях этих уравнений, которые
численно равны отношению возвращающей силы при единичном смещении к массе
колеблющегося тела и имеют размерность [с-2]. Если использовать
обозначения
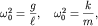 | (1.5) |
то уравнения (1.4) примут вид уравнения незатухающих гармонических
колебаний, или уравнения гармонического осциллятора:
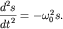 | (1.6) |
Решением уравнения (1.6) является семейство гармонических функций
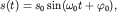 | (1.7) |
в чем легко убедиться, дважды продифференцировав функцию 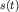 по времени: по времени:
Заметим, что если уравнение движения приводится к виду (1.6), то его
решением являются гармонические функции (1.7) с частотой 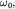 равной корню квадратному из коэффициента при
равной корню квадратному из коэффициента при  . .
Значения этих гармонических функций в начальный момент времени (при 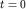 )
определяются начальной фазой )
определяются начальной фазой 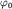 (см. ниже) и амплитудой
колебаний (см. ниже) и амплитудой
колебаний 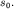 У одной и той же системы эти значения могут быть
различными при разных способах возбуждения колебаний. У одной и той же системы эти значения могут быть
различными при разных способах возбуждения колебаний.
Чтобы возбудить собственные колебания, надо вначале (при 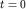 ) либо
отклонить тело (задать начальное смещение ) либо
отклонить тело (задать начальное смещение 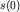 ), либо толкнуть его (задать
начальную скорость ), либо толкнуть его (задать
начальную скорость 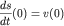 ), либо сделать и то, и
другое одновременно. Знание начальных условий (смещения и скорости)
позволяет определить амплитуду ), либо сделать и то, и
другое одновременно. Знание начальных условий (смещения и скорости)
позволяет определить амплитуду 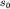 и начальную фазу колебаний и начальную фазу колебаний 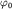 из очевидных уравнений: из очевидных уравнений:
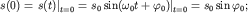 | (1.8) |
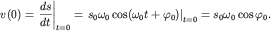 | (1.9) |
Решение этих уравнений имеет вид:
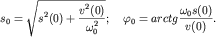 | (1.10) |
Важно отметить, что амплитуда колебаний 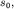 равная величине
максимального смещения тела от положения равновесия, может превосходить
начальное смещение равная величине
максимального смещения тела от положения равновесия, может превосходить
начальное смещение 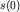 при наличии начального толчка. при наличии начального толчка.
Наряду с круговой частотой 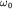 колебания характеризуются
циклической частотой колебания характеризуются
циклической частотой  равной числу
колебаний за единицу времени, и периодом колебаний равной числу
колебаний за единицу времени, и периодом колебаний 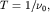 равным длительности одного колебания.
равным длительности одного колебания.
Период гармонических колебаний (равно как и частоты 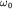 и и 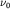 ) не зависит от начальных условий и равен ) не зависит от начальных условий и равен
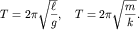 | (1.11) |
Другим примером являются колебания физического маятника - тела
произвольной формы массы  , закрепленного на горизонтальной оси {\displaystyle O}' так,
что его центр масс находится в точке O, удаленной от оси на расстояние , закрепленного на горизонтальной оси {\displaystyle O}' так,
что его центр масс находится в точке O, удаленной от оси на расстояние  .
При отклонении маятника от вертикали на небольшой угол .
При отклонении маятника от вертикали на небольшой угол  он будет
совершать свободные гармонические колебания под действием силы тяжести,
приложенной к центру масс (рис. 1.2). он будет
совершать свободные гармонические колебания под действием силы тяжести,
приложенной к центру масс (рис. 1.2).
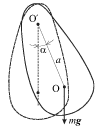 | | Рис. 1.2. |
Если известен момент инерции тела  относительно оси вращения, то уравнение
вращательного движения запишется в виде относительно оси вращения, то уравнение
вращательного движения запишется в виде
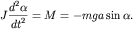 | (1.12) |
Если считать, что при вращении, например, против часовой стрелки угол
 увеличивается, то момент силы тяжести увеличивается, то момент силы тяжести 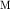 вызывает уменьшение этого
угла и, следовательно, при вызывает уменьшение этого
угла и, следовательно, при 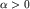 момент момент 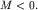 Это и отражает знак
минус в правой части (1.12). Это и отражает знак
минус в правой части (1.12).
Для малых углов отклонения уравнение (1.12) переходит в уравнение
гармонических колебаний
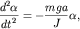 | (1.13) |
из вида которого сразу ясно, что частота 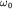 и период и период  колебаний
соответственно равны колебаний
соответственно равны
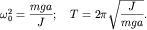 | (1.14) |
Сравнивая выражения для периода колебаний физического (1.14) и
математического (1.11) маятников, легко видеть, что оба периода совпадают, если
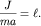 | (1.15) |
Поэтому физический маятник характеризуется приведенной длиной (1.15),
которая равна длине математического маятника с таким же периодом колебаний.
Период колебаний физического маятника (а, следовательно, и его приведенная
длина  ) немонотонно зависит от расстояния ) немонотонно зависит от расстояния  . Это легко заметить, если
в соответствии с теоремой Гюйгенса-Штейнера момент инерции . Это легко заметить, если
в соответствии с теоремой Гюйгенса-Штейнера момент инерции 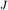 выразить через
момент инерции выразить через
момент инерции 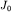 относительно параллельной горизонтальной оси,
проходящей через центр масс: относительно параллельной горизонтальной оси,
проходящей через центр масс: 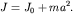 Тогда период колебаний
(1.14) будет равен: Тогда период колебаний
(1.14) будет равен:
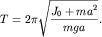 | (1.16) |
Изменение периода колебаний при удалении оси вращения от центра масс O в обе
стороны на расстояние а показано на рис. 1.3.
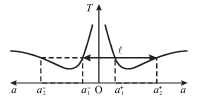 | | Рис. 1.3. |
Легко видеть, что один и тот же период колебаний может реализоваться
относительно любой из четырех осей, расположенных попарно по разные стороны
от центра масс. Можно показать, что сумма расстояний 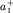 и и
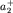 равна приведенной длине физического маятника: равна приведенной длине физического маятника: 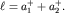 В силу симметрии графика ясно, что В силу симметрии графика ясно, что
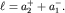 | (1.17) |
Это обстоятельство позволяет для любой оси вращения O+ определить
сопряженную ось O-. Период колебаний относительно этих осей одинаков,
а расстояние между ними равно приведенной длине физического маятника.
На рис. 1.4 изображены положения осей O+ и O-, при этом ось
вращения, удаленная на расстояние 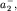 при такой форме маятника
находится вне его. при такой форме маятника
находится вне его.
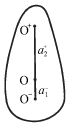 | | Рис. 1.4. |
Физический маятник применяется для измерения ускорения свободного падения. С
этой целью измеряют зависимость периода колебаний маятника от положения оси
вращения и по этой экспериментальной зависимости находят в соответствии с
формулой (1.17) приведенную длину. Определенная таким образом приведенная
длина в сочетании с измеренным с хорошей точностью периодом колебаний
относительно обеих осей позволяет рассчитать ускорение свободного падения.
Важно отметить, что при таком способе измерений не требуется определение
положения центра масс, что в ряде случаев повышает точность измерений.
Назад| Вперед
Посмотреть комментарии[2]
| 
