Если грузы, изображенные на рис. 3.5а, сместить на произвольные расстояния
(например, в одну сторону на величины  и и  как это
изображено на рис. 3.5б), то это эквивалентно суперпозиции двух типов
начальных смещений: в одну сторону на одинаковые величины (позиция в) как это
изображено на рис. 3.5б), то это эквивалентно суперпозиции двух типов
начальных смещений: в одну сторону на одинаковые величины (позиция в)
 | | (3.10)
и в разные стороны (позиция г) на величины
 | | (3.11)
Поскольку колебательная система линейна, то синфазные колебания, возникающие
после отпускания грузов в позиции (в), будут происходить независимо от
присутствия противофазных колебаний, возникающих при отпускании грузов в
позиции (г). Смещения обоих грузов с течением времени будут описываться
формулами (3.5), в которых амплитуды определяются равенствами (3.10) и
(3.11), а начальные фазы 
 | | Рис. 3.5. |
Проанализируем более подробно колебания в системе, изображенной на рис. 3.5.
Пусть мы сдвинули левую массу вправо на расстояние  а правую массу
оставим в несмещенном положении а правую массу
оставим в несмещенном положении  После отпускания обоих
грузов в системе возникнут колебания. Из (3.10) и (3.11) определяем
амплитуды мод: После отпускания обоих
грузов в системе возникнут колебания. Из (3.10) и (3.11) определяем
амплитуды мод:  Поскольку фазы Поскольку фазы  (т.к. начальные скорости у грузов отсутствуют), то смещения (т.к. начальные скорости у грузов отсутствуют), то смещения
 | | (3.12)
Производя суммирование тригонометрических функций в (3.12), получим:
 | | (3.13)
Временные зависимости (3.13) изображены на рис. 3.6.
 | | Рис. 3.6. |
Видно, что колебания каждой из масс имеют форму биений. Период этих биений
равен1
 | | (3.14)
где частота биений
 | | (3.15)
Если ввести среднюю частоту
 | | (3.16)
то с этой частотой связан период колебаний 
Если частота биений  как это изображено на
рис. 3.6, то как это изображено на
рис. 3.6, то  В этом случае колебания обоих грузов будут почти
гармоническими (квазигармоническими). Если переписать (3.13) с
использованием средней частоты В этом случае колебания обоих грузов будут почти
гармоническими (квазигармоническими). Если переписать (3.13) с
использованием средней частоты 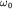 и частоты биений и частоты биений  в виде:
в виде:
 | | (3.17)
то при  колебания (3.17) можно трактовать как
колебания с частотой колебания (3.17) можно трактовать как
колебания с частотой 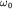 и медленно меняющейся амплитудой и медленно меняющейся амплитудой 
В теории колебаний и в других разделах физики для анализа колебательного
процесса используют спектральное представление, или спектр колебаний. Этот
спектр изображают графически, где по оси абсцисс указывают частоты
колебаний, а по оси ординат откладывают квадраты их амплитуд. Так, в
частности, для колебаний, изображенных на рис. 3.6 (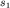 или или 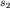 ) и
описываемых формулами (3.17), легко нарисовать спектр, поскольку уже
известно спектральное разложение этого колебания (представление в виде суммы
гармонических колебаний), задаваемое формулами (3.12). ) и
описываемых формулами (3.17), легко нарисовать спектр, поскольку уже
известно спектральное разложение этого колебания (представление в виде суммы
гармонических колебаний), задаваемое формулами (3.12).
Такой спектр изображен на рис. 3.7.
 | | Рис. 3.7. |
Этот спектр содержит две спектральные компоненты. Его можно охарактеризовать
средней частотой 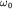 и шириной и шириной  В соответствии с
формулой (3.14) произведение В соответствии с
формулой (3.14) произведение 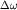 на период на период  равно
постоянной величине: равно
постоянной величине:
 | | (3.18)
Формула (3.18) имеет глубокое физическое содержание. Так, если происходит
некоторое квазигармоническое колебание вида
![$ s(t) = A(t)\cos [\omega _{0} t + \varphi (t)], $](http://images.nature.web.ru/nature/2001/11/27/0001175042/tex/formula320.gif) | | (3.19)
для которого амплитуда  и фаза и фаза  медленно меняются на масштабе
времени медленно меняются на масштабе
времени  (рис. 3.8а), то спектр такого колебания может состоять из
большого числа частот. (рис. 3.8а), то спектр такого колебания может состоять из
большого числа частот.
 | | Рис. 3.8. |
Эти частоты группируются вблизи центральной (основной) частоты  в пределах характерного интервала частот в пределах характерного интервала частот  обратно пропорционального временному масштабу
обратно пропорционального временному масштабу  На рис. 3.8б
изображен этот спектр, где по оси ординат отложен квадрат амплитуды На рис. 3.8б
изображен этот спектр, где по оси ординат отложен квадрат амплитуды 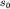 каждой из гармонических составляющих, причем между
каждой из гармонических составляющих, причем между  и и 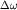 существует связь:
существует связь: 
Количественная связь между колебательным процессом 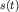 и его спектром
представляется (по аналогии с формулами (3.12)) в виде суммы конечного или
бесконечного числа гармонических составляющих (в виде ряда или интеграла
Фурье). Такое представление будет широко использоваться в курсе "Оптика". и его спектром
представляется (по аналогии с формулами (3.12)) в виде суммы конечного или
бесконечного числа гармонических составляющих (в виде ряда или интеграла
Фурье). Такое представление будет широко использоваться в курсе "Оптика".
1Колебания (3.12), вообще говоря, не являются периодическими, т.е.
нельзя указать такое время  спустя которое они точно повторяются
(отношение частот спустя которое они точно повторяются
(отношение частот  - чаще всего иррациональное
число, а случаи их рационального отношения: - чаще всего иррациональное
число, а случаи их рационального отношения:  будут исчезающе редки). Поэтому периодом биений
будут исчезающе редки). Поэтому периодом биений  мы называем период
(3.14) повторения огибающей суммарного колебания, равный половине периода
колебания с частотой мы называем период
(3.14) повторения огибающей суммарного колебания, равный половине периода
колебания с частотой 
Назад| Вперед
Посмотреть комментарии[2]
| 
