Выше было дано определение энергии Ферми
EF для металлов, как максимальной энергии электронов при
T=0.
Химический потенциал  определяется как энергия
состояния, вероятность заполнения которого равна 1/2. определяется как энергия
состояния, вероятность заполнения которого равна 1/2.
Для металлов при Т=0 и энергия Ферми
Е и химический потенциал и химический потенциал  совпадают. совпадают.
С ростом температуры кинетическая энергия электронного газа увеличивается,
электроны занимают энергетические состояния, которые при Т=0 были
свободны. Часть энергетических состояний, которые при Т=0 были
заняты, становятся свободными. (рис.2).
При низких температурах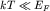 , граница заполнения энергетических
состояний размывается симметрично относительно значения , граница заполнения энергетических
состояний размывается симметрично относительно значения 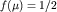 на величину порядка 2кТ (рис.2в). При этом
на величину порядка 2кТ (рис.2в). При этом  практически,
совпадает с практически,
совпадает с 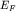 и вероятность заполнения электроном
состояния на уровне Ферми (т.е. с энергий и вероятность заполнения электроном
состояния на уровне Ферми (т.е. с энергий 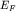 ) равна: ) равна: 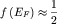 . .
При дальнейшем повышении температуры размытие становится несимметричным
(рис. 2б) и значение химического потенциала смещается в область низких
энергий. В этой области температур система характеризуется значением
химического потенциала, а не энергией Ферми.
Литература: [А.Н.Матвеев, 1987,  14-16] 14-16]
Смещение химического потенциала вырожденного электронного газа с ростом
температуры в области низких температур можно вычислить с помощью
изложенного выше метода для расчета средних значений.
При любой температуре число электронов в металле остается постоянным. Это
условие, учитывая выражения для n (2.2) и (2.3), запишем как
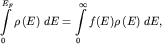 | (2.12) |
Для интеграла правой части уравнения (2.12) используем соотношение (2.11)
при 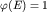 . Тогда вспомогательная функция . Тогда вспомогательная функция 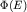 и ее производные на основании (2.8) определятся
соотношениями: и ее производные на основании (2.8) определятся
соотношениями:
Таким образом (2.12) примет вид
или 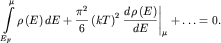
При низких температурах, когда \mu находится вблизи значения 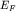 , приближенно можно записать: , приближенно можно записать:
или ![$\mu \cong E_{ F} {\displaystyle \left[ {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \pi ^{ 2}}}{\displaystyle {\displaystyle 6}}}\left( {\displaystyle kT} \right)^{ 2}{\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle \rho \left( {\displaystyle E_{ F} } \right)}}}{\displaystyle \mathop {\displaystyle {\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle d\rho \left( {\displaystyle E} \right)}}{\displaystyle {\displaystyle dE}}}} \right|}}\nolimits_{ \mu } }} \right]}.$](http://images.nature.web.ru/nature/2001/11/16/0001174320/tex/formula731.gif)
Учитывая зависимость 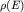 (2.4) получим окончательный
результат в виде: (2.4) получим окончательный
результат в виде:
![$ \mu \cong E_{ F} {\displaystyle \left[ {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \pi ^{ 2}}}{\displaystyle {\displaystyle 12}}}\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle kT}}{\displaystyle {\displaystyle E_{ F} }}}} \right)^{ 2}} \right]} $](http://images.nature.web.ru/nature/2001/11/16/0001174320/tex/formula732.gif) | (2.13) |
Так как при низких температурах 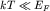 , то можно
заключить, что смещение химического потенциала , то можно
заключить, что смещение химического потенциала  с ростом температуры
имеет второй порядок малости. с ростом температуры
имеет второй порядок малости.
Литература: [А.Н.Матвеев, 1987,  16; Дж.Займан, 1966, гл.4, 16; Дж.Займан, 1966, гл.4,  5] 5]
Для электронов с энергиями
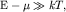 | (2.14) |
то есть на "хвостах" распределения Ферми-Дирака, выражение (1.16)
соответствует большим значениям экспоненты в знаменателе. Тогда единицей
можно пренебречь и функция распределения для таких электронов принимает вид
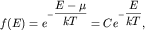 | (2.15) |
Она совпадает с функцией распределения Гиббса для частиц, подчиняющихся
классической статистике Максвелла-Больцмана, когда число доступных
состояний значительно больше числа частиц, способных занять эти состояния.
Химический потенциал понижается с ростом температуры Т. Число
электронов, описываемых статистикой Максвелла-Больцмана, растет. Чтобы
условие (2.11) выполнялось для всех электронов, то есть, чтобы все электроны
системы описывались статистикой Максвелла-Больцмана, энергия каждого
электрона должна превышать  , то есть химический потенциал должен стать
отрицательным , то есть химический потенциал должен стать
отрицательным 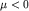 . .
Электронный газ, подчиняющийся статистике Максвелла-Больцмана,
называется невырожденным, а - подчиняющийся статистике Ферми -
Дирака, называется вырожденным. Температура
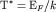 | (2.16) |
называется температурой вырождения или температурой
Ферми.
При 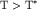 ступенчатый характер распределения меняется на
экспоненциальный. ступенчатый характер распределения меняется на
экспоненциальный.
Электроны проводимости практически всех металлов находятся в состоянии
сильного вырождения. При этом электроны, находящиеся вблизи уровня Ферми,
имеют энергию, значительно превосходящую кинетическую энергию их теплового
движения.
Литература: [А.Н.Матвеев, 1987,  16] 16]
В термодинамике химический потенциал определяет среднее вероятностное
изменение энергии системы частиц при изменении числа частиц на единицу. Он
равен производной по числу частиц в системе от внутренней энергии 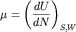 при постоянном объеме W
и энтропии S (или любого другого термодинамического потенциала -
свободной энергии F, энтальпии H или потенциала Гиббса
G, соответственно, при постоянном объеме W
и энтропии S (или любого другого термодинамического потенциала -
свободной энергии F, энтальпии H или потенциала Гиббса
G, соответственно, 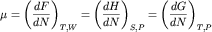 , где P - давление). Можно показать, что
статистическое и термодинамическое определения химического потенциала
совпадают [6]. , где P - давление). Можно показать, что
статистическое и термодинамическое определения химического потенциала
совпадают [6].
При выводе распределения Ферми-Дирака определение (статистическое)
химического потенциала  было сделано аналогично статистическому
определению температуры. Как и температура, химический потенциал было сделано аналогично статистическому
определению температуры. Как и температура, химический потенциал  является функцией состояния и одинаков во всех частях
термодинамической системы, находящейся в состоянии равновесия. Это относится
и к случаю, когда термодинамическая система неоднородна. Например, при
наложении внешнего статического поля или при контакте двух проводников
происходит перераспределение электронов таким образом, чтобы химический
потенциал стал одинаковым во всех частях системы. Выравнивание уровней
химических потенциалов следует из термодинамического условия достижения
максимума энтропии полной системы. Химический потенциал необходим для
описания открытых систем, когда число частиц в системе может меняться.
является функцией состояния и одинаков во всех частях
термодинамической системы, находящейся в состоянии равновесия. Это относится
и к случаю, когда термодинамическая система неоднородна. Например, при
наложении внешнего статического поля или при контакте двух проводников
происходит перераспределение электронов таким образом, чтобы химический
потенциал стал одинаковым во всех частях системы. Выравнивание уровней
химических потенциалов следует из термодинамического условия достижения
максимума энтропии полной системы. Химический потенциал необходим для
описания открытых систем, когда число частиц в системе может меняться.
Термодинамическое определение химического потенциала  позволяет
наглядно описать положение и смещение позволяет
наглядно описать положение и смещение  при изменении температуры в
металлах и полупроводниках (см. ниже 4.3). при изменении температуры в
металлах и полупроводниках (см. ниже 4.3).
Величину химического потенциала для электронной системы можно
оценить, как изменение энергии системы при внесении одной частицы, одного
электрона. При этом вносимый электрон приобретает возможность занимать
те же свободные энергетические состояния, что и электроны системы.
Для металлов вносимый электрон при Т=0, занимая
свободное состояние с минимально возможным значением энергии, помещается на
сферу Ферми с энергией 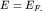 Таким образом, химический потенциал
совпадает с энергией Ферми Таким образом, химический потенциал
совпадает с энергией Ферми 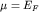 . .
Литература: [А.Н.Матвеев, 1987,  40; Ч.Киттель, 1978, стр.490] 40; Ч.Киттель, 1978, стр.490]
Назад| Вперед
Написать комментарий
| 
