Как известно все вещества по характеру электропроводности делятся на три
основных класса: металлы, полупроводники и диэлектрики.
Характерной особенностью металлов является их металлическая
проводимость - увеличение проводимости при понижении температуры при
постоянной концентрации носителей тока.
У чистых полупроводников их собственная проводимость экспоненциально
уменьшается при понижении температуры и обращается в нуль при 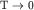 , что
указывает на то, что носители тока в полупроводниках появляются только в
результате термического возбуждения. , что
указывает на то, что носители тока в полупроводниках появляются только в
результате термического возбуждения.
В диэлектриках свободные носители тока вообще отсутствуют.
Различие в электрических свойствах этих трех классов веществ определяется,
прежде всего, характером химических связей между атомами решетки.
Возможны два характерных предельных случая. В первом случае валентные электроны находятся
на внешних атомных s- и p-орбиталях, которые слабо связаны с атомными
остовами. Во втором случае валентные электроны находятся на внутренних 3d-, 4d-, 5d- и
4f-электронных оболочках.
В первом случае перекрытие волновых функций столь сильно, что электроны практически
полностью утрачивают свою s- и p- специфику и коллективизируются, то
есть перестают быть связанными с отдельными атомами кристаллической решетки
и приобретают способность перемещаться в ней. Такие электроны в первом
приближении можно рассматривать почти свободными (модель свободных
электронов или приближение слабой связи (см. 2)) и описывать плоскими
волнами, слабо модулированными периодическим потенциалом решетки.
Во втором случае, поскольку размеры d- и f-орбиталей существенно меньше, чем внешних s- и
p-орбиталей, перекрытие оказывается достаточно слабым, так что d- и f-
специфика электронов в значительной степени сохраняется. Волновые функции
таких коллективизированных электронов описывать плоскими волнами не
корректно. В этом случае при построении энергетического спектра следует
исходить из невозмущенных, локализованных на отдельных атомах
электронных состояний и рассматривать их изменение из-за
взаимодействия, возникающего при сближении атомов. Такой подход получил
название модели сильной связи (или приближения сильной связи
(см. 3)).
Моделью слабой связи хорошо описываются все непереходные металлы с заполненными внутренними d- и
f-орбиталями. Моделью сильной связи - переходные и редкоземельные металлы, у которых металлическая
проводимость возникает в результате отсутствия энергетической щели между
связывающими и разрыхляющими зонами или в результате перекрытия зон.
Практически во всех атомарных полупроводниках и диэлектриках, имеющих аналогичную кристаллическую структуру
и отличающихся различной шириной запрещенной зоны (у диэлектриков она
больше), электроны описываются локализованными, связанными молекулярными
орбиталями. Таким образом, их следует рассматривать в рамках модели сильной
связи.
По современным представлениям металл можно рассматривать как
совокупность системы большого числа N положительно заряженных
колеблющихся ионов, образующих квазипериодическую пространственную структуру
(кристаллическую решетку), и системы относительно свободных
коллективизированных валентных электронов, не локализованных
вблизи отдельных ионов, а перемещающихся по всему кристаллу. Отличие
одного металла от другого связано с разной валентностью z атомов,
особенностями их электронной структуры, а также с симметрией кристаллической
решетки.
Теоретическое описание металла в рамках такой модели приводит к
квантовомеханической задаче о системе (N+zN) взаимодействующих между
собой частиц. Строгое решение такой задачи в настоящее время невозможно.
Качественное представление о характере поведения электронов, их
энергетическом спектре можно получить на основании следующих
приближений.
Адиабатическое приближение.
Массы ионов, образующих кристаллическую решетку, и массы электронов, а,
следовательно, и скорости их движения, сильно различаются (скорости -
приблизительно на два-три порядка). Поэтому можно, считать, что, во-первых,
движение электронов не зависит от движения ионов и, во-вторых, ионы в узлах
решетки неподвижны и образуют строго периодическую
кристаллическую решетку. Такое приближение называют адиабатическим
или приближением Борна-Оппенгеймера.
Одноэлектронное приближение.
Взаимодействие электронов друг с другом можно заменить взаимодействием
каждого электрона с усредненным полем всех остальных электронов. Это поле
определяет не только движение данного электрона, но и само зависит от его
движения, то есть является самосогласованным полем. Введение
самосогласованного поля позволяет рассматривать электроны в кристалле как
почти не взаимодействующие частицы. Полная энергия при этом равна сумме
энергий отдельных электронов. Таким образом, самосогласованное поле
позволяет задачу многих частиц свести к задаче для одного электрона
(одноэлектронное приближение).
При этом электрон не является совсем свободным, так как находится в
потенциальном поле всех ионов решетки и самосогласованном поле других
электронов.
Литература: [А.Н.Матвеев, 1987,  14-16; Н.Б.Брандт, С.М.Чудинов, 1990, ч.II, гл1, 14-16; Н.Б.Брандт, С.М.Чудинов, 1990, ч.II, гл1,  4; Дж.Займан, 1966, гл.3, 4; Дж.Займан, 1966, гл.3,  1; Ч.Киттель, 1978, гл.3; К.В.Шалимова, 1985, 1; Ч.Киттель, 1978, гл.3; К.В.Шалимова, 1985,  2.2] 2.2]
Благодаря кулоновскому полю положительно заряженных ионов полная энергия
электронов в кристалле ниже, чем в вакууме на величину, определяющую работу
выхода электронов при внешнем фотоэффекте. Поэтому кристалл для электронов
можно рассматривать как потенциальный ящик, ограниченный поверхностью
кристалла, с постоянным значением потенциала внутри объема кристалла.
Как было показано в п.I.3 ограничение движения электронов приводит к тому,
что непрерывный энергетический спектр Е=р2/(2m)
становится дискретным с квантованными значениями импульса (1.19) и энергии
(1.22).
Будем рассматривать в дальнейшем кристалл единичного объема
LxLyLz=W=1. В таком кристалле
число (концентрация) коллективизированных электронов равна
n=zN, где N - число атомов, z - их валентность.
Согласно принципу Паули для ферми-частиц, в каждом состоянии, занимающем
объем в p-пространстве равный 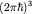 (1.21), может
находиться только два электрона с противоположно направленными спинами. При
абсолютном нуле температуры электроны занимают самые низкие энергетические
состояния. Это утверждение согласуется с распределением Ферми-Дирака (1.16),
когда при Т=0 вероятность заполнения состояний с энергией
( (1.21), может
находиться только два электрона с противоположно направленными спинами. При
абсолютном нуле температуры электроны занимают самые низкие энергетические
состояния. Это утверждение согласуется с распределением Ферми-Дирака (1.16),
когда при Т=0 вероятность заполнения состояний с энергией
(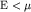 ) ниже химического потенциала ) ниже химического потенциала  равна единице, а
выше, при равна единице, а
выше, при 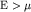 , - нулю. , - нулю.
Таким образом, при Т=0 электроны заполняют в
p-пространстве сферу (рис.6), радиус которой
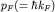 определяется из равенства числа
электронов zN удвоенному (за счет спиновых состояний) числу
элементарных квантовых ячеек (1.21) в объеме определяется из равенства числа
электронов zN удвоенному (за счет спиновых состояний) числу
элементарных квантовых ячеек (1.21) в объеме 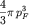 сферы, то есть сферы, то есть
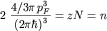 | (2.1) |
Максимально возможные значения импульса p_{ F} и соответствующей
ему энергии E_{ F} электронов при T=0, называются,
соответственно, импульсом и энергией Ферми.
Изоэнергетическая (E=E_{ F}=const.)
поверхность (или совокупность поверхностей см. ниже) в пространстве
импульсов, внутри которой все состояния заполнены при Т=0, называется
поверхностью Ферми. Импульс и энергия Ферми на основании (2.1)
определяются следующими соотношениями:
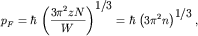 | (2.2) |
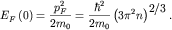 | (2.3) |
Таким образом, энергия Ферми растет с увеличением концентрации
коллективизированных электронов пропорционально n2 / 3.
Литература: [А.Н.Матвеев, 1987,  14-16; А.Н.Матвеев, 1987, 14-16; А.Н.Матвеев, 1987,  2; Н.Б.Брандт, С.М.Чудинов, 1990,ч.2,гл.1, 2; Н.Б.Брандт, С.М.Чудинов, 1990,ч.2,гл.1,  1,гл.5, 1,гл.5,  1; Дж.Займан, 1966, гл.3, 1; Дж.Займан, 1966, гл.3,
 1; Ч.Киттель, 1978,гл.7;] 1; Ч.Киттель, 1978,гл.7;]
Назад| Вперед
Написать комментарий
|

