N12. Тепловой слой электронов. Оценить какая
доля электронов зоны проводимости кобальта находится в возбужденных
состояниях при температуре плавления, если энергия Ферми у кобальта равна
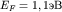 ? Температура плавления кобальта ? Температура плавления кобальта 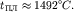
Решение: Рассмотрим кристалл единичного объема. Для оценки примем
следующие приближения.
Положим значение химического потенциала для температур вблизи температуры плавления приблизительно равным значению энергии Ферми 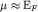 .
Плотность состояний .
Плотность состояний 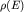 вблизи уровня Ферми слабо изменяется вблизи уровня Ферми слабо изменяется 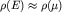 . Так как полное число электронов . Так как полное число электронов 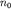 в зоне проводимости равно (2.1) в зоне проводимости равно (2.1) 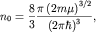 то на основании (2.4а) можно записать то на основании (2.4а) можно записать
Ступеньку распределения Ферми-Дирака заменим линейной зависимостью (1.17):
Тогда число возбужденных электронов, находящихся выше энергии Ферми,
оценивается как
что составляет от полного числа электронов
Ответ: 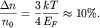
N13 Теплоемкость электронного газа [А.Н.Матвеев, 1987,  16; Дж.Займан, 1966, гл.4, 16; Дж.Займан, 1966, гл.4,  7; Ч.Киттель, 1978, гл.7]. Показать, что теплоемкость электронного газа в
металлах пропорциональна температуре. 7; Ч.Киттель, 1978, гл.7]. Показать, что теплоемкость электронного газа в
металлах пропорциональна температуре.
Решение. Электроны в металле вырождены. Это значит, что к ним не
применимо распределение Максвелла-Больцмана и теорема о равнораспределении
энергии по степеням свободы, которая позволяет легко рассчитать теплоемкость
идеального газа.
Поскольку электронный газ вырожден, то тепловой энергией 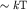 обладают только электроны, находящиеся в слое толщины
обладают только электроны, находящиеся в слое толщины 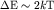 (1.17) вблизи поверхности Ферми. Число электронных состояний в
этом слое на основании (2.4) равно (1.17) вблизи поверхности Ферми. Число электронных состояний в
этом слое на основании (2.4) равно
где учтено, что полное число электронов определяется соотношением (2.1)
Таким образом, полная энергия всех тепловых электронов равна
и пропорциональна 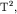 а молярная теплоемкость при постоянном
объеме а молярная теплоемкость при постоянном
объеме
пропорциональна температуре. Более точные расчеты дают для молярной
теплоемкости значение 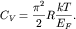
Теплоемкость металлов при нормальных условиях близка к 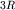 по закону
Дюлонга и Пти. Поскольку в этих условиях по закону
Дюлонга и Пти. Поскольку в этих условиях 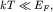 то
электронная теплоемкость пренебрежимо мала по сравнению с решеточной
теплоемкостью. Однако при низких температурах, когда теплоемкость решетки
подчиняется закону Дебая и уменьшается с температурой пропорционально то
электронная теплоемкость пренебрежимо мала по сравнению с решеточной
теплоемкостью. Однако при низких температурах, когда теплоемкость решетки
подчиняется закону Дебая и уменьшается с температурой пропорционально 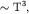 электронная теплоемкость может превосходить решеточную. электронная теплоемкость может превосходить решеточную.
N14. Теплоемкость электронного газа. Известно, что у
массивных металлов электронная теплоемкость во всей области температур
пропорциональна температуре (см. задачу N13). Как изменится температурная
зависимость теплоемкости для маленьких металлических частичек одновалентного
металла с простой кубической решеткой c периодом 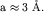 Размер частичек имеет порядок Размер частичек имеет порядок 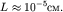
Решение. Для малых частиц существенным может оказаться квантование
энергии в зоне. Определим характерную температуру 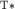 , при которой
расстояние между энергетическими уровнями , при которой
расстояние между энергетическими уровнями  сравнится с тепловой энергией
сравнится с тепловой энергией 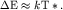 Используя результат задачи N5, получим Используя результат задачи N5, получим
что соответствует температуре 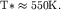
Таким образом, при температурах ниже 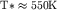 число тепловых
электронов число тепловых
электронов 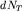 будет определяться характерным
больцмановским множителем будет определяться характерным
больцмановским множителем 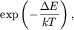 что приведет к экспоненциальной зависимости теплоемкости от
температуры что приведет к экспоненциальной зависимости теплоемкости от
температуры 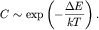 Число тепловых электронов можно оценить как
Число тепловых электронов можно оценить как 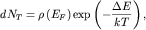 их энергия -
их энергия - 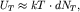 а теплоемкость
а теплоемкость
Ответ: при температурах ниже 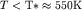 теплоемкость
будет иметь экспоненциальный характер теплоемкость
будет иметь экспоненциальный характер 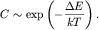
N15 Фермиевская скорость электронов.
Определить фермиевскую скорость электронов в одномерном металле с одним
электроном на элементарную ячейку и законом дисперсии
![$E=E _{ o} [1-cos(k _{ x} a)],$](http://images.nature.web.ru/nature/2001/11/16/0001174320/tex/formula528.gif) где где 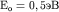 и и
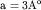 ( ( 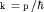 - волновой вектор). - волновой вектор).
Решение. Так как по определению скорость электрона 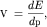 то фермиевская скорость при законе дисперсии то фермиевская скорость при законе дисперсии
![$E=E _{ o} [cos(k _{ x} a)-1]$](http://images.nature.web.ru/nature/2001/11/16/0001174320/tex/formula533.gif) запишется в виде запишется в виде
Фермиевский импульс связан с концентрацией электронов  следующими
соотношениями. следующими
соотношениями.
В трехмерном случае - 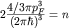 и и 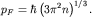 | (1) |
В двумерном - 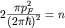 и и 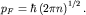 | (2) |
В одномерном - 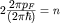 и и 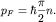 | (3) |
Поскольку по условию задачи на элементарную ячейку приходится один электрон,
то энергетическая зона заполнена наполовину и концентрация равна
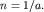 Учитывая также, что в одномерном случае Учитывая также, что в одномерном случае 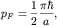 получим получим 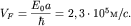
Ответ: 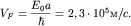
N16 Фермиевская скорость электронов. Вычислить
фермиевскую скорость электронов в двумерном металле с квадратной решеткой,
если закон дисперсии электронов имеет вид 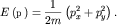 Площадь
элементарной ячейки в плоскости решетки равна Площадь
элементарной ячейки в плоскости решетки равна 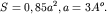 Считать, что на элементарную ячейку приходится
один электрон проводимости, а масса Считать, что на элементарную ячейку приходится
один электрон проводимости, а масса 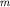 равна массе свободного
электрона. равна массе свободного
электрона.
Решение. аналогично задаче 15 при условии (2). Поскольку
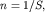 то из соотношения (2) получим то из соотношения (2) получим 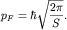 Модуль скорости электронов на поверхности Ферми
будет равен Модуль скорости электронов на поверхности Ферми
будет равен
Фермиевский импульс можно найти иначе, определив сначала объем (площадь)
зоны Бриллюэна, так как он связан с объемом (площадью) элементарной ячейки в
двумерном случае соотношением 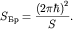 Так как по условию задачи на элементарную ячейку
приходится один электрон, то энергетическая зона заполнена наполовину и
фермиевский импульс определится из условия Так как по условию задачи на элементарную ячейку
приходится один электрон, то энергетическая зона заполнена наполовину и
фермиевский импульс определится из условия 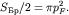
Ответ: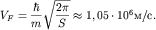
Назад| Вперед
Написать комментарий
| 
