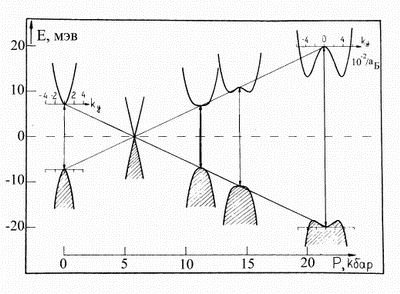
Зонная структура энергетического спектра вещества может изменяться под
воздействием внешних параметров: давления, магнитного поля, состава и т.д.
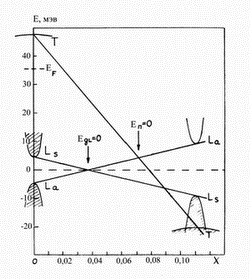
Для наглядности на рисунке 39 приведена, полученная на основании
экспериментальных данных [Г.А.Миронова, 1979] диаграмма перестройки энергетического
спектра сплавов Bi1 - xSbx при изменении
концентрации сурьмы в интервале 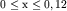 . Первая
зона Бриллюэна для Bi и Sb близка по форме к зоне Бриллюэна для
гранецентрированной решетки (рис.19б). В висмуте энергетическая щель в точке
L (рис.39) при х=0 мала . Первая
зона Бриллюэна для Bi и Sb близка по форме к зоне Бриллюэна для
гранецентрированной решетки (рис.19б). В висмуте энергетическая щель в точке
L (рис.39) при х=0 мала 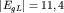 мэВ и
наблюдается перекрытие валентной зоны, расположенной в точке T с зоной
проводимости в точке L. мэВ и
наблюдается перекрытие валентной зоны, расположенной в точке T с зоной
проводимости в точке L.
 | | Рис. 39. |
Поскольку в висмуте реализуется структура с двумя атомами в элементарной
ячейке, то, без перекрытия зон висмут был бы собственным полупроводником с
полностью заполненной валентной зоной и пустой зоной проводимости. При
перекрытии зон часть электронов из валентной зоны перетекает в зону
проводимости, в результате чего висмут является полуметаллом (аналогичная
ситуация рассмотрена в 2.8, рис.22). Три электронные поверхности Ферми у
висмута и сурьмы находятся в центрах шестигранников зоны Бриллюэна (точки
L на рис.19а) в виде трех эллипсоидов. Дырочная поверхность Ферми
близкая по форме к эллипсоиду вращения у Bi расположена в точке T.
Уровень Ферми у Bi лежит на 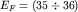 мэВ выше дна зоны
проводимости в точке L (см. рис.39 при х=0). мэВ выше дна зоны
проводимости в точке L (см. рис.39 при х=0).
При легировании висмута сурьмой границы зон смещаются (рис.39): потолок
валентной зоны в точке Т смещается вниз относительно дна зоны
проводимости в точке L. При этом величина перекрытия и,
соответственно, концентрации электронов и дырок уменьшаются. При
концентрации сурьмы х=0,07 перекрытие обращается в нуль
(Еп =0). При больших концентрациях (х>0,07)в спектре
образуется энергетическая щель и сплав становится собственным
полупроводником. На рисунке 39 изображены экстремумы энергетических зон для
полупроводникового сплава Bi1 - xSbx при 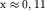 . .
Энергетическая щель у полупроводниковых сплавов Bi1 - xSbx (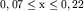 ) не превосходит 30мэВ. Поэтому эти сплавы относятся
к классу узкощелевых полупроводников. ) не превосходит 30мэВ. Поэтому эти сплавы относятся
к классу узкощелевых полупроводников.
Аналогичная перестройка энергетического спектра происходит
под действием давления. На рисунке 40
показана перестройка спектра полупроводникового сплава Bi1 - xSbx
(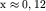 ) с прямой энергетической щелью ) с прямой энергетической щелью 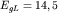 мэВ под
действием давления. Энергетическая щель мэВ под
действием давления. Энергетическая щель 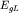 уменьшается под
действием давления и при некотором критическом давлении обращается в нуль.
При этом давлении сплав переходит в новое состояние, которое получило
название бесщелевого. Это состояние является промежуточным между
полуметаллом и полупроводником. Его можно рассматривать как предельный
случай полуметалла с вырожденными в точки изоэнергетическими поверхностями
или как предельный случай полупроводника с нулевой прямой щелью между
зонами. В бесщелевом состоянии вещество приобретает новые свойства,
качественно отличающие его от металлов и полупроводников. Например, в этом
состоянии эффективные массы электронов на дне зоны проводимости и дырок у
потолка валентной зоны обращаются в нуль. уменьшается под
действием давления и при некотором критическом давлении обращается в нуль.
При этом давлении сплав переходит в новое состояние, которое получило
название бесщелевого. Это состояние является промежуточным между
полуметаллом и полупроводником. Его можно рассматривать как предельный
случай полуметалла с вырожденными в точки изоэнергетическими поверхностями
или как предельный случай полупроводника с нулевой прямой щелью между
зонами. В бесщелевом состоянии вещество приобретает новые свойства,
качественно отличающие его от металлов и полупроводников. Например, в этом
состоянии эффективные массы электронов на дне зоны проводимости и дырок у
потолка валентной зоны обращаются в нуль.
 | | Рис. 40. |
Ряд задач, которые, по мнению автора, имеют самостоятельный интерес или
методическое значение, сопровождается решением.
N1. Распределение Ферми-Дирака. Пусть  . Показать, что функция распределения Ферми-Дирака
удовлетворяет условию: . Показать, что функция распределения Ферми-Дирака
удовлетворяет условию:
N2. Распределение Ферми-Дирака. Вычислить
функцию распределения Ферми-Дирака для  где
где 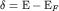 . Для . Для 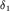 оценить погрешность,
допускаемую при линеаризации ступеньки в виде оценить погрешность,
допускаемую при линеаризации ступеньки в виде 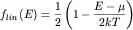 . .
Ответ: 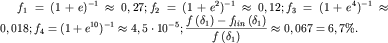
N3 Распределение Ферми-Дирака. Используя
зависимость (2.13) 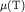 в области низких температур, получите
выражение для функции распределения Ферми-Дирака в области низких температур, получите
выражение для функции распределения Ферми-Дирака 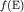 для
заданной температуры и оцените во сколько раз изменится вероятность
состояния с энергией для
заданной температуры и оцените во сколько раз изменится вероятность
состояния с энергией 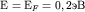 при изменении температуры от при изменении температуры от
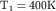 до до 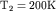 . .
Ответ:
N4 Химический потенциал для двумерного Ферми-газа.
Получите точное (интегральное) уравнение для химического потенциала 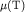 для двумерного идеального электронного газа. для двумерного идеального электронного газа.
Ответ: 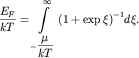
N5 Дискретность энергии в зоне. Оценить приблизительно
размер металлической частицы, для которой максимальное расстояние между
уровнями в энергетической зоне может быть существенным. Указание:
найти число атомов, при котором максимальное расстояние между
энергетическими уровнями было бы равно  при
1 при
1 К. К.
Решение. Импульс электрона в металле принимает дискретные значения,
что связано с ограниченностью движения электронов размерами кристалла:
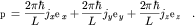 Квант импульса равен Квант импульса равен |
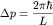 | (1) |
Соответствующее расстояние между энергетическими уровнями
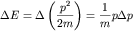 | (2) |
увеличивается с ростом импульса и максимально для электронов с импульсом
Ферми.
На основании (2.2) фермиевский импульс равен
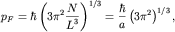 | (3) |
где 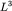 - объем кристалла, - объем кристалла, 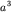 - объем элементарной
ячейки, - объем элементарной
ячейки, 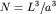 - число атомов в кристалле. - число атомов в кристалле.
Подставляя в (2) 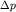 и и 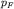 , соответственно,
из (1) и (3), получим , соответственно,
из (1) и (3), получим
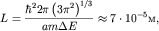 | (4) |
где межатомное расстояние а для оценки полагалось равным а
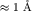
Ответ: 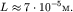
N6. Фермиевский импульс. Для одновалентного
металла с простой кубической решеткой с периодом 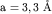 определить фермиевский импульс
определить фермиевский импульс 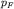 и минимальное расстояние и минимальное расстояние
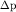 от поверхности Ферми до границы зоны Бриллюэна. Какая
часть зоны заполнена электронами? Найти отношение от поверхности Ферми до границы зоны Бриллюэна. Какая
часть зоны заполнена электронами? Найти отношение 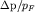 . .
Решение. На основании (2.2) фермиевский импульс равен
где 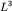 - объем кристалла, - объем кристалла, 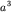 - объем элементарной
ячейки, - объем элементарной
ячейки, 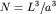 - число атомов в кристалле.
Первая зона Бриллюэна представляет собой куб со стороной - число атомов в кристалле.
Первая зона Бриллюэна представляет собой куб со стороной 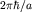 в импульсном пространстве. Отсюда получаем в импульсном пространстве. Отсюда получаем
Ответ: 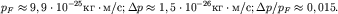 Заполнена половина зоны. Заполнена половина зоны.
Назад| Вперед
Написать комментарий
| 
