Волновые функции  , описывающие состояние электронов в атомах часто
называются атомными орбиталями. Волновая функция
1s-состояния симметрична относительно ядра атома и имеет вид , описывающие состояние электронов в атомах часто
называются атомными орбиталями. Волновая функция
1s-состояния симметрична относительно ядра атома и имеет вид
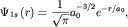 | (3.3) |
где r - расстояние от ядра.
Состояния с l=1, p-состояния, описываются тремя
(2l+1=3) независимыми волновыми функциями 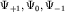 , для которых магнитные квантовые числа равны,
соответственно, m=+1, m=0, m=-1. Наиболее часто
волновые функции p-состояний записывают в виде линейных комбинаций: , для которых магнитные квантовые числа равны,
соответственно, m=+1, m=0, m=-1. Наиболее часто
волновые функции p-состояний записывают в виде линейных комбинаций:
Волновые функции p-состояний зависят уже не только от r, но и
от 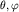 - углов, задаваемых в сферической системе
координат. Например, для j=2 волновые функции 2px-,2 py- и 2pz- состояний имеют следующий вид: - углов, задаваемых в сферической системе
координат. Например, для j=2 волновые функции 2px-,2 py- и 2pz- состояний имеют следующий вид:
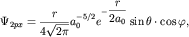 | (3.4) |
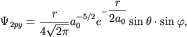 | (3.5) |
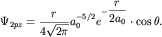 | (3.6) |
Пространственное распределение 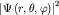 описывает распределение плотности вероятности
нахождения электрона около ядра, то есть плотности отрицательного заряда в
околоядерном пространстве. В такой интерпретации электрон
рассматривается как некоторое пространственное образование - электронное
облако. описывает распределение плотности вероятности
нахождения электрона около ядра, то есть плотности отрицательного заряда в
околоядерном пространстве. В такой интерпретации электрон
рассматривается как некоторое пространственное образование - электронное
облако.
Волновая функция, например, 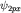 имеет разные знаки:
положительный при x>0, т.е. в интервале углов ( имеет разные знаки:
положительный при x>0, т.е. в интервале углов ( 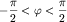 ) и отрицательный при x<0,
т.е. для углов ( ) и отрицательный при x<0,
т.е. для углов ( 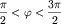 )
(3.4). Однако описываемое ею распределение электронной плотности )
(3.4). Однако описываемое ею распределение электронной плотности 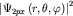 не зависит от знака функции и представляет собой электронное облако, вытянутое вдоль оси
x (см. (3.4)). не зависит от знака функции и представляет собой электронное облако, вытянутое вдоль оси
x (см. (3.4)).
Широко употребляемый способ изображения волновых функций - полярные
диаграммы (r=const.), на которых изображается угловая
часть волновой функции. Внутри каждой области полярных диаграмм ставится
знак волновой функции.
На рисунке 26 для примера приведены полярные диаграммы
- s-орбитали (а) -
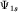 (3.3); (3.3);
- p-орбиталей: (б) -
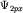 (3.4); (в) - (3.4); (в) - 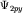 (3.5); (г) - (3.5); (г) - 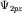 (3.6); (3.6);
- d-орбиталей: (д) -
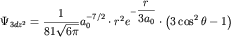 ; (е) - ; (е) - 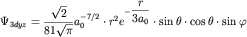 [Д.Г.Кнорре и др., 1990, [Д.Г.Кнорре и др., 1990,  3.1]. 3.1].
Литература: [Р.Фейнман и др., 1967, гл.17,  5; Д.Г.Кнорре и др., 1990, 5; Д.Г.Кнорре и др., 1990,  3.1] 3.1]
Основные изменения состояний электронов, возникающие при сближении атомов и
образовании кристаллической структуры, можно проиллюстрировать на простой
модели связывания атома водорода и протона в двухатомную систему -
молекулярный ион Н2+.
При приближении протона к атому водорода потенциальная энергия системы
изменяется на величину
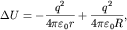 | (3.7) |
связанную с электростатическим притяжением электрона атома водорода к
приближающемуся протону и отталкиванием между протонами. Расстояния r
и R (3.7) изображены на рисунке 27, где справа от плоскости Н,
перпендикулярной отрезку Р1Р2, находится атом водорода Р1, а слева - протон Р2.
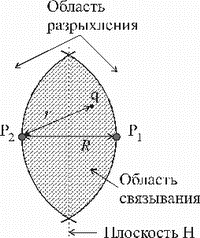 | | Рис. 27. |
Знак 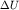 зависит от расстояния r электрона до
протона. При зависит от расстояния r электрона до
протона. При 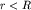 , то есть когда электрон находится в заштрихованной
на рисунке области, называемой областью связывания, потенциальная энергия
системы (3.7) уменьшается , то есть когда электрон находится в заштрихованной
на рисунке области, называемой областью связывания, потенциальная энергия
системы (3.7) уменьшается 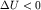 . Если электрон находится в
области r>R (область разрыхления), то потенциальная энергия . Если электрон находится в
области r>R (область разрыхления), то потенциальная энергия 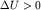 растет. растет.
Волновые функции (атомные орбитали) 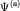 и и 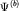 электронных состояний вблизи отдельных протонов P1 и P2,
соответственно, при сближении начинают перекрываться. Количественной
характеристикой степени перекрытия волновых функций является интеграл
перекрытия
электронных состояний вблизи отдельных протонов P1 и P2,
соответственно, при сближении начинают перекрываться. Количественной
характеристикой степени перекрытия волновых функций является интеграл
перекрытия
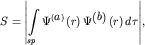 | (3.8) |
в котором интегрирование производится по всему пространству (sp).
Интеграл перекрытия имеет максимальное значение в области перекрытия
волновых функций и мал вне этой области.
При наличии перекрытия (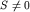 ) электрон не может рассматриваться
как принадлежащий одному из атомов. При этом по мере сближения атомные
орбитали видоизменяются и называются молекулярными орбиталями. Из
двух атомных орбиталей, например, ) электрон не может рассматриваться
как принадлежащий одному из атомов. При этом по мере сближения атомные
орбитали видоизменяются и называются молекулярными орбиталями. Из
двух атомных орбиталей, например, 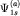 , , 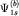 атомов (a) и (b) образуются, соответственно, две молекулярные
орбитали:
атомов (a) и (b) образуются, соответственно, две молекулярные
орбитали:
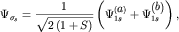 | (3.9) |
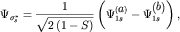 | (3.10) |
где S- интеграл перекрытия (3.8), а множитель перед скобками,
содержащий S, следует из условий нормировки:
Для 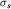 -молекулярной орбитали электронная плотность равна -молекулярной орбитали электронная плотность равна
При сближении атомов электронная плотность растет в области перекрытия, где
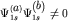 , за
счет уменьшения электронной плотности вне области перекрытия. Таким образом,
происходит концентрирование электронной плотности в пространстве между
ядрами. Энергия , за
счет уменьшения электронной плотности вне области перекрытия. Таким образом,
происходит концентрирование электронной плотности в пространстве между
ядрами. Энергия 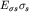 -электронного
состояния ниже энергии электрона в изолированном атоме -электронного
состояния ниже энергии электрона в изолированном атоме 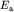 на на
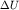 (3.7). (3.7). 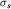 -орбиталь называется
связывающей молекулярной орбиталью. -орбиталь называется
связывающей молекулярной орбиталью.
Для 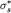 -молекулярной орбитали электронная плотность,
определяемая соотношением -молекулярной орбитали электронная плотность,
определяемая соотношением
по мере сближения атомов и роста интеграла перекрытия уменьшается в области,
где 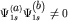 ,
по сравнению с суммой плотностей ,
по сравнению с суммой плотностей ![${\displaystyle \left[ {\displaystyle \left( {\displaystyle \Psi _{ 1s}^{ \left( {\displaystyle a} \right)} } \right)^{ 2} + \left( {\displaystyle \Psi _{ 1s}^{ \left( {\displaystyle a} \right)} } \right)^{ 2}} \right]}$](http://images.nature.web.ru/nature/2001/11/16/0001174320/tex/formula146.gif) исходных атомных орбиталей. Электронная плотность за
счет роста исходных атомных орбиталей. Электронная плотность за
счет роста 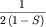 увеличивается в области
разрыхления. увеличивается в области
разрыхления.
Следовательно, энергия 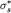 - орбитали выше - орбитали выше
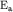 , так как , так как 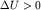 . Связанные состояния на таких
орбиталях не осуществляются. . Связанные состояния на таких
орбиталях не осуществляются. 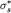 -орбиталь
называется разрыхляющей молекулярной орбиталью. -орбиталь
называется разрыхляющей молекулярной орбиталью.
Видоизменение 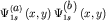 (3.3) орбиталей при
сближении атомов и образование молекулярных орбиталей (3.3) орбиталей при
сближении атомов и образование молекулярных орбиталей 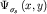 и и 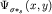 наглядно иллюстрируется диаграммами, представленными на рис28а. На
рисунке 28б представлены диаграммы атомных орбиталей наглядно иллюстрируется диаграммами, представленными на рис28а. На
рисунке 28б представлены диаграммы атомных орбиталей 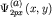 и и 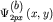 (3.4), и диаграммы (3.4), и диаграммы  связывающей и связывающей и 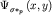 - разрыхляющей молекулярных орбиталей, иллюстрирующие
форму электронных облаков получающихся в результате перекрытия атомных
орбиталей. Оси оx и oy соответствуют рисункам 26а,б, причем ось
оx проходит через центры атомов (a) и (b). - разрыхляющей молекулярных орбиталей, иллюстрирующие
форму электронных облаков получающихся в результате перекрытия атомных
орбиталей. Оси оx и oy соответствуют рисункам 26а,б, причем ось
оx проходит через центры атомов (a) и (b).
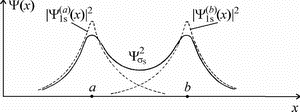
На рисунке 29а представлены электронные плотности 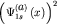 и и 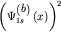 исходных атомных
орбиталей и плотность исходных атомных
орбиталей и плотность 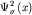 молекулярной молекулярной
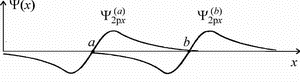
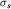 -орбитали в зависимости от координаты x. На рисунке
29б изображены волновые функции -орбитали в зависимости от координаты x. На рисунке
29б изображены волновые функции 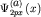 и и 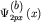 (3.4) двух
соседних атомов (а) и (b). (3.4) двух
соседних атомов (а) и (b).
 |  | | а | б | | Рис. 29. |
Литература: [Д.Г.Кнорре и др., 1990,  4.1, 4.1,  4.2] 4.2]
Назад| Вперед
Написать комментарий
| 
