Next: 9. Заключение
Up: 8. Класс IP
Previous: 8.3.
Contents: Содержание
Дадим набросок доказательства, подробно это
доказательство изложено в книге Сипсера [9].
Достаточно доказать, что
 -полная задача -полная задача
 принадлежит принадлежит
 . .
Итак, пусть нужно проверить истинность высказывания

в котором
 - некоторая логическая формула, - некоторая логическая формула,
 , кванторы действуют на формулы по
правилам (14)-(15). , кванторы действуют на формулы по
правилам (14)-(15).
Оценить истинность высказывания  можно следующей рекурсивной
процедурой. Обозначим через можно следующей рекурсивной
процедурой. Обозначим через
 высказывание высказывание

Тогда
 , где , где  - связка, определяемая
квантором - связка, определяемая
квантором
 . Найдем вначале . Найдем вначале  , а затем , а затем  , каждый
раз вызывая рекурсивно саму описываемую процедуру
(для определения , каждый
раз вызывая рекурсивно саму описываемую процедуру
(для определения
 достаточно вычислить значение
формулы достаточно вычислить значение
формулы
 , так что рекурсия конечная)
и вычислим , так что рекурсия конечная)
и вычислим
 . .
Эта процедура требует вычисления всех  возможных значений
формулы возможных значений
формулы
 , а потому занимает экспоненциально
большое по сравнению с размером входа задачи время. Наглядно это
вычисление можно изобразить в виде дерева, как показано на
рис. 4а. В процессе вычисления мы получаем не только
значение в корне, но и значения во всех промежуточных узлах дерева,
количество которых экспоненциально велико. , а потому занимает экспоненциально
большое по сравнению с размером входа задачи время. Наглядно это
вычисление можно изобразить в виде дерева, как показано на
рис. 4а. В процессе вычисления мы получаем не только
значение в корне, но и значения во всех промежуточных узлах дерева,
количество которых экспоненциально велико.
Чем может помочь Советник в таком вычислении? Он, конечно,
может сообщить значение  . Впрочем, поскольку Советник
пристрастен, то в любом случае он скажет, что . Впрочем, поскольку Советник
пристрастен, то в любом случае он скажет, что  . Попробуем
проверить это сообщение и запросим значения . Попробуем
проверить это сообщение и запросим значения  и и  -
должно выполняться соотношение -
должно выполняться соотношение
 . Далее
выберем случайно и равновероятно число . Далее
выберем случайно и равновероятно число  , запросим у
Советника значения , запросим у
Советника значения  и и  , проверим , проверим
 и т. д. На последнем шаге уже без
всякого Советника можно проверить, что и т. д. На последнем шаге уже без
всякого Советника можно проверить, что

Вычисления будут длиться
 тактов, где
тактов, где  - количество тактов, необходимых для вычисления
значения логической формулы длины - количество тактов, необходимых для вычисления
значения логической формулы длины 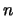 при заданных значениях
переменных. Они происходят вдоль одного из путей от корня к листьям в
дереве на рис. 4а, выбираемого случайно и равновероятно. при заданных значениях
переменных. Они происходят вдоль одного из путей от корня к листьям в
дереве на рис. 4а, выбираемого случайно и равновероятно.
Рис. 4.
 |
С какой вероятностью Исполнитель принимает решение об
истинности QBF? Если рассматриваемая формула истинна, то Советнику
достаточно говорить истинные значения всех запрашиваемых величин,
Исполнитель не увидит никакого противоречия и с вероятностью 1
признает формулу истинной.
Что будет, если QBF ложна? Чтобы
убедить Исполнителя в обратном, Советнику хотя бы раз придется солгать,
сообщив неверное значение одной из пары запрашиваемых переменных. Эта
ложь с вероятностью 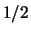 замечена не будет, что показывает
непригодность описанной процедуры для надежного определения истинности
QBF. замечена не будет, что показывает
непригодность описанной процедуры для надежного определения истинности
QBF.
Как ни странно, есть способ исправить описанную выше процедуру.
Если в исходном варианте из полного бинарного дерева перебора
случайно выбирался один путь, и это ничего не дало, то в исправленной
версии дерево станет шире (каждый раз будет выбор из 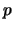 вариантов,
где вариантов,
где  - простое число)
и глубже (глубина дерева была - простое число)
и глубже (глубина дерева была  , а в
исправленной версии будет примерно , а в
исправленной версии будет примерно  ). Это дерево изображено
на рис. 4б. ). Это дерево изображено
на рис. 4б.
Чтобы построить такое разветвленное дерево, будем считать
истинностные значения  и и  элементами поля элементами поля
 вычетов по модулю вычетов по модулю 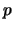 . Любую
логическую формулу . Любую
логическую формулу
 можно записать как многочлен
можно записать как многочлен
 над полем
над полем  ,
используя выражения (8). Степень ,
используя выражения (8). Степень
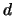 этого многочлена не превосходит длины записи формулы этого многочлена не превосходит длины записи формулы
 , которая меньше , которая меньше
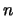 - размера входа задачи - размера входа задачи
 . .
Кванторам сопоставим следующие операции с многочленами:
 |
(17) |
 |
(18) |
Теперь число
 |
(19) |
равняется истинностному значению формулы
 (
( - операция, соответствующая квантору - операция, соответствующая квантору
 ).
Вычисление этого числа организовано в дерево, аналогичное изображенным
на рис. 4. Степень ветвления у этого дерева равна ).
Вычисление этого числа организовано в дерево, аналогичное изображенным
на рис. 4. Степень ветвления у этого дерева равна 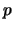 , а
глубина - , а
глубина -  . .
Высказываниям
 при этом соответствуют многочлены при этом соответствуют многочлены

Заметим, что операции  , ,  уменьшают число переменных
на 1, но удваивают, вообще говоря, степень каждой из
оставшихся переменных, так что степени уменьшают число переменных
на 1, но удваивают, вообще говоря, степень каждой из
оставшихся переменных, так что степени  могут быть велики.
Чтобы степени многочленов не росли чрезмерно при вычислениях, можно
воспользоваться
следующей операцией: могут быть велики.
Чтобы степени многочленов не росли чрезмерно при вычислениях, можно
воспользоваться
следующей операцией:
 |
(20) |
Многочлены 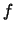 и и  имеют одинаковое количество переменных,
совпадают при имеют одинаковое количество переменных,
совпадают при  , а степень переменной , а степень переменной 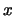 в в  равна 1.
равна 1.
Итак, истинностное
значение высказывания  равно равно

где  определяется по входу задачи определяется по входу задачи
 (так же, как
в (19)). К многочлену (так же, как
в (19)). К многочлену  применяются в заданном
порядке применяются в заданном
порядке  операций вида операций вида  , ,  или или  . Пусть
после применения первых . Пусть
после применения первых  операций получается многочлен операций получается многочлен
 , ,  . Поскольку операция . Поскольку операция  не
меняет количества переменных в многочлене,
число не
меняет количества переменных в многочлене,
число  не обязательно равно не обязательно равно 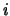 . .
Теперь опишем диалог между Исполнителем и Советником.
Начинается он с того, что Советник сообщает
значение  (как и раньше, в самом начале он скажет, что (как и раньше, в самом начале он скажет, что  независимо от его настоящего значения). Затем Исполнитель спрашивает у
Советника, чему равен многочлен
независимо от его настоящего значения). Затем Исполнитель спрашивает у
Советника, чему равен многочлен  . Получив коэффициенты этого
многочлена, Исполнитель проверяет, что . Получив коэффициенты этого
многочлена, Исполнитель проверяет, что
 (будем
операцию, стоящую на (будем
операцию, стоящую на 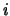 -м месте обозначать -м месте обозначать  ).
После этого Исполнитель
случайно и равновероятно выбирает число ).
После этого Исполнитель
случайно и равновероятно выбирает число  и
применяет рекурсивно ту же процедуру для проверки равенства и
применяет рекурсивно ту же процедуру для проверки равенства

Конечность рекурсии обеспечивается тем, что значение
многочлена
 Исполнитель вычисляет
самостоятельно. Если все проверки дают положительный результат,
Исполнитель выдает в качестве ответа 1, если хотя бы раз обнаружено
неравенство - 0. Исполнитель вычисляет
самостоятельно. Если все проверки дают положительный результат,
Исполнитель выдает в качестве ответа 1, если хотя бы раз обнаружено
неравенство - 0.
Теперь оценим вероятности ответа 1.
Если рассматриваемая QBF истинна, то Советнику опять
достаточно говорить истинные значения всех запрашиваемых величин.
А вот если
QBF ложна, Советнику хотя бы
раз придется солгать. Поскольку два многочлена степени  совпадают не более чем в
совпадают не более чем в 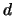 точках, то с вероятностью не меньшей точках, то с вероятностью не меньшей
 на следующем шаге будет проверяться ложное условие.
По индукции получаем, что вероятность обнаружить ложь в
описанном диалоге не меньше на следующем шаге будет проверяться ложное условие.
По индукции получаем, что вероятность обнаружить ложь в
описанном диалоге не меньше

где  - общее количество проверок.
При - общее количество проверок.
При  эта вероятность будет близка к 1. эта вероятность будет близка к 1.
Next: 9. Заключение
Up: 8. Класс IP
Previous: 8.3.
Contents: Содержание
Написать комментарий
|

