Next: 8.4.
Up: 8. Класс IP
Previous: 8.2. Определение класса IP
Contents: Содержание
Определение
 похоже на уголовно-процессуальное
определение класса похоже на уголовно-процессуальное
определение класса
 . И доказательство . И доказательство
 напоминает ту часть доказательства теоремы 5, в которой
строится алгоритм определения выигрышной стратегии, использующий
полиномиально ограниченную память.
напоминает ту часть доказательства теоремы 5, в которой
строится алгоритм определения выигрышной стратегии, использующий
полиномиально ограниченную память.
Пусть
 .
Снова по индукции определяется набор
машин Тьюринга .
Снова по индукции определяется набор
машин Тьюринга  для для
 . .
Каждая  по заданному
началу диалога по заданному
началу диалога
 длины длины  между Исполнителем и
Советником оценивает вероятность ответа между Исполнителем и
Советником оценивает вероятность ответа  при продолжении диалога.
Последняя в этом ряду машина при продолжении диалога.
Последняя в этом ряду машина  имитирует
работу Исполнителя, вычисляет функцию имитирует
работу Исполнителя, вычисляет функцию
 и сообщает
в качестве ответа ее значение.
Машина и сообщает
в качестве ответа ее значение.
Машина  перебирает все возможные варианты
перебирает все возможные варианты  -го сообщения и
консультируется с -го сообщения и
консультируется с  по поводу окончательных результатов. Если
слово за Советником, то оценка по поводу окончательных результатов. Если
слово за Советником, то оценка  - максимум оценок - максимум оценок  по
всем возможным вариантам сообщения Советника. Если слово за
Исполнителем, то оценка по
всем возможным вариантам сообщения Советника. Если слово за
Исполнителем, то оценка  равна среднему арифметическому оценок равна среднему арифметическому оценок
 по всем по всем  (это формула полной вероятности). (это формула полной вероятности).
Алгоритм вычисления 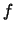 на полиномиальной памяти запускает на полиномиальной памяти запускает  и выдает в качестве результата 1, если оценка
и выдает в качестве результата 1, если оценка  больше
больше 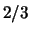 , и 0, если оценка , и 0, если оценка  меньше меньше 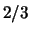 . .
Написать комментарий
| 
