Next: 8. Класс IP
Up: Сложность вычислительных задач
Previous: 6.4. 3-раскраска
Contents: Содержание
Как уже говорилось,
в этот класс попадают те функции, которые могут быть вычислены на МТ,
использующей память, ограниченную полиномом от длины входного слова.
Этот класс включает в себя класс  (за время (за время  мы сможем
использовать память, не превосходящую мы сможем
использовать память, не превосходящую  ) и класс ) и класс
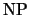 (диалог
Советника с Исполнителем занимает полиномиальное время, поэтому
Исполнитель, не ограниченный во времени, может перебрать по очереди
все
варианты записей такого диалога, используя для этого сравнительно
небольшую - ограниченную полиномом от длины входа - память). Но
класс (диалог
Советника с Исполнителем занимает полиномиальное время, поэтому
Исполнитель, не ограниченный во времени, может перебрать по очереди
все
варианты записей такого диалога, используя для этого сравнительно
небольшую - ограниченную полиномом от длины входа - память). Но
класс
 , по-видимому, гораздо шире чем , по-видимому, гораздо шире чем
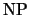 . К сожалению,
доказать это никому до сих пор не удалось. . К сожалению,
доказать это никому до сих пор не удалось.
Классу
 , точнее говоря, характеристическим
функциям, входящим в , точнее говоря, характеристическим
функциям, входящим в
 , можно дать следующее неформальное
описание. Представим несколько идеализированную модель
судопроизводства. Слово , можно дать следующее неформальное
описание. Представим несколько идеализированную модель
судопроизводства. Слово 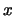 - описание некоторого дела,
находящегося на рассмотрении суда, который должен вынести вердикт:
виновен ли обвиняемый (значение характеристической функции равно 1).
Судья - уже знакомый нам полиномиально ограниченный Исполнитель (он
будет работать время, не превосходящее полинома от длины описания
дела). Есть также Прокурор, настаивающий на виновности обвиняемого, и
Адвокат, убеждающий судью в обратном. Оба они интеллектуально всемогущи
и по очереди приводят свои аргументы. Правила ведения судебного
разбирательства зафиксированы в Уголовно-Процессуальном Кодексе. Судья
подводит итог разбирательства, основываясь на описании дела - описание некоторого дела,
находящегося на рассмотрении суда, который должен вынести вердикт:
виновен ли обвиняемый (значение характеристической функции равно 1).
Судья - уже знакомый нам полиномиально ограниченный Исполнитель (он
будет работать время, не превосходящее полинома от длины описания
дела). Есть также Прокурор, настаивающий на виновности обвиняемого, и
Адвокат, убеждающий судью в обратном. Оба они интеллектуально всемогущи
и по очереди приводят свои аргументы. Правила ведения судебного
разбирательства зафиксированы в Уголовно-Процессуальном Кодексе. Судья
подводит итог разбирательства, основываясь на описании дела 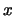 , на
состоявшейся дискуссии между Прокурором и Адвокатом и на УПК (т. е. по
сути вычисляет значение некоторой полиномиально вычислимой функции,
определяемой УПК, на входе, описывающем судебное разбирательство -
слово , на
состоявшейся дискуссии между Прокурором и Адвокатом и на УПК (т. е. по
сути вычисляет значение некоторой полиномиально вычислимой функции,
определяемой УПК, на входе, описывающем судебное разбирательство -
слово 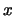 , текст первого выступления Прокурора, текст первого выступления
Адвоката, текст второго выступления Прокурора и т. д.). , текст первого выступления Прокурора, текст первого выступления
Адвоката, текст второго выступления Прокурора и т. д.).
В таком экстравагантном контексте класс
 определяется следующим образом: характеристическая функция
определяется следующим образом: характеристическая функция 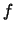 принадлежит
принадлежит
 , если можно придумать такой УПК, что при , если можно придумать такой УПК, что при
 у Прокурора есть стратегия ведения дискуссии,
которая убеждает Судью в виновности обвиняемого при любых вариантах
действий Адвоката; а при у Прокурора есть стратегия ведения дискуссии,
которая убеждает Судью в виновности обвиняемого при любых вариантах
действий Адвоката; а при  аналогичная стратегия есть у
Адвоката. аналогичная стратегия есть у
Адвоката.
Замечание 5.
Обычно описанную выше модель излагают в более нейтральных
терминах. Говорят об игре двух лиц, зависящей от входного слова, и
существовании выигрышной стратегии у одного из игроков.
Теорема 5.
Стандартное и уголовно-процессуальное определения класса
 равносильны. равносильны.
Доказательство.
Покажем, что язык из
 в смысле УПК
принадлежит в смысле УПК
принадлежит
 в смысле стандартного определения. Пусть число
выступлений сторон ограничено в смысле стандартного определения. Пусть число
выступлений сторон ограничено  . Определим по индукции набор
машин Тьюринга . Определим по индукции набор
машин Тьюринга  для для
 . Каждая . Каждая  по заданному
началу дискуссии по заданному
началу дискуссии
 длины длины  определяет наличие
убеждающей стратегии для Прокурора. Последней в этом ряду машине определяет наличие
убеждающей стратегии для Прокурора. Последней в этом ряду машине  нужно просто проимитировать работу Судьи и вычислить
функцию нужно просто проимитировать работу Судьи и вычислить
функцию
 . Машина . Машина
 перебирает все возможные варианты перебирает все возможные варианты  -го выступления и
консультируется с -го выступления и
консультируется с  по поводу окончательных результатов
судебного разбирательства. Ее оценка перспектив разбирательства
составляется очень просто: если текущее выступление за Прокурором,
то достаточно найти хотя бы один вариант выступления, после
которого по поводу окончательных результатов
судебного разбирательства. Ее оценка перспектив разбирательства
составляется очень просто: если текущее выступление за Прокурором,
то достаточно найти хотя бы один вариант выступления, после
которого  гарантирует убеждающую стратегию
для Прокурора. Если текущее выступление за Адвокатом, то после любого
из возможных выступлений гарантирует убеждающую стратегию
для Прокурора. Если текущее выступление за Адвокатом, то после любого
из возможных выступлений
 должна обнаружить убеждающую стратегию для Прокурора.
Машина должна обнаружить убеждающую стратегию для Прокурора.
Машина  определяет наличие убеждающей стратегии
для Прокурора в самом начале процесса и для ее работы нужно
задействовать всю последовательность машин определяет наличие убеждающей стратегии
для Прокурора в самом начале процесса и для ее работы нужно
задействовать всю последовательность машин  . Но каждая из этих
машин использует небольшую (полиномиально ограниченную) память, так что
весь процесс потребует лишь полиномиально ограниченной памяти. . Но каждая из этих
машин использует небольшую (полиномиально ограниченную) память, так что
весь процесс потребует лишь полиномиально ограниченной памяти.
А теперь покажем обратное.
Пусть есть машина 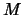 , вычисляющая некоторую характеристическую функцию , вычисляющая некоторую характеристическую функцию
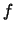 на полиномиальной памяти.
Заметим прежде всего, что вычисление на памяти на полиномиальной памяти.
Заметим прежде всего, что вычисление на памяти  бессмысленно
проводить дольше, чем время бессмысленно
проводить дольше, чем время  (все начнет повторяться после
того, как мы исчерпаем все состояния нашей системы, а их не более чем (все начнет повторяться после
того, как мы исчерпаем все состояния нашей системы, а их не более чем
 , где , где
 -
соответственно множество состояний управляющего устройства и
алфавит рассматриваемой МТ). Поэтому можно считать без ограничения
общности, что время работы машины -
соответственно множество состояний управляющего устройства и
алфавит рассматриваемой МТ). Поэтому можно считать без ограничения
общности, что время работы машины 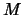 ограничено ограничено  ,
где ,
где  . .
Для простоты описания потребуем, чтобы
после завершения вычисления МТ сохраняла без изменений достигнутое
состояние.
Правила судебной дискуссии состоят в следующем.
Прокурор утверждает, что на входном слове 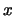 машина выдает
результат 1, а Адвокат подвергает это сомнению.
В первом своем выступлении Прокурор обязан описать
состояние машины машина выдает
результат 1, а Адвокат подвергает это сомнению.
В первом своем выступлении Прокурор обязан описать
состояние машины 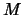 (строка, записанная на ленте, положение читающей головки, состояние
управляющего устройства) после
(строка, записанная на ленте, положение читающей головки, состояние
управляющего устройства) после  тактов работы. В
ответном слове Адвокат указывает на один из
промежутков: от начала до тактов работы. В
ответном слове Адвокат указывает на один из
промежутков: от начала до  -го такта или от -го такта или от  -го
такта до конца. После этого Прокурор обязан описать
состояние -го
такта до конца. После этого Прокурор обязан описать
состояние 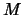 в середине этого промежутка. Далее все повторяется:
Адвокат выбирает одну из половинок, Прокурор описывает состояние в середине этого промежутка. Далее все повторяется:
Адвокат выбирает одну из половинок, Прокурор описывает состояние
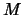 в середине выбранной половинки и т. д. в середине выбранной половинки и т. д.
Дискуссия заканчивается, когда длина промежутка становится равной 1.
Судья подводит итог так: в течение процесса
для обоих концов этого промежутка
были описаны состояния 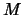 , если состояние
правого конца получается из состояния левого конца за один такт работы , если состояние
правого конца получается из состояния левого конца за один такт работы
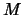 , то Судья склоняется к мнению Прокурора, в противном
случае - к мнению Адвоката. Необходимые проверки займут у Судьи
время, полиномиально ограниченное длиной входного слова. , то Судья склоняется к мнению Прокурора, в противном
случае - к мнению Адвоката. Необходимые проверки займут у Судьи
время, полиномиально ограниченное длиной входного слова.
Пусть  . Тогда убеждающая стратегия для Прокурора состоит в
том, чтобы каждый раз сообщать истинное положение дел (напомним, что
Прокурор интеллектуально всемогущ, так что он в состоянии
промоделировать в уме работу машины . Тогда убеждающая стратегия для Прокурора состоит в
том, чтобы каждый раз сообщать истинное положение дел (напомним, что
Прокурор интеллектуально всемогущ, так что он в состоянии
промоделировать в уме работу машины 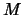 ). ).
Пусть  . Тогда, что бы ни говорил Прокурор,
на одном из промежутков (или на обоих) будет содержаться
ошибка. Адвокат должен указывать
каждый раз именно такой промежуток - это гарантирует ему успех. . Тогда, что бы ни говорил Прокурор,
на одном из промежутков (или на обоих) будет содержаться
ошибка. Адвокат должен указывать
каждый раз именно такой промежуток - это гарантирует ему успех.

В классе
 существуют полные относительно полиномиальной
сводимости задачи. Простейший вариант получается из
приведенного выше доказательства. существуют полные относительно полиномиальной
сводимости задачи. Простейший вариант получается из
приведенного выше доказательства.
Задача
TQBF
(Truth of Quantified
Boolean Formula).
Задается предикатом
По определению кванторы действуют на формулы следующим естественным
образом:
 |
(14) |
 |
(15) |
Теорема 6.
Задача TQBF
 -полна. -полна.
Итог описанной выше дискуссии
можно выразить в виде квантифицированной формулы, если
записать условие "одно состояние МТ получается
из другого за один такт" в виде логической формулы.
Хотя в этой дискуссии
выступления были длиннее чем в один бит, их нетрудно превратить в
однобитовые, вставляя после каждого бита настоящего выступления одной
из сторон фантомное выступление противоположной стороны
("покашливание"). Формула  от "покашливаний" не
зависит. от "покашливаний" не
зависит.
Next: 8. Класс IP
Up: Сложность вычислительных задач
Previous: 6.4. 3-раскраска
Contents: Содержание
Написать комментарий
|

