Next: 6.4. 3-раскраска
Up: 6. Примеры NP-полных задач
Previous: 6.2. Разрешимость системы уравнений
Contents: Содержание
Теперь
разберем задачу из примера 2, т. е. разрешимость
системы линейных диофантовых уравнений в неотрицательных числах.
Замечание 4.
Название "линейное программирование" относится к задачам
минимизации линейной функции на множестве решений системы линейных
неравенств. Слово "целочисленное" указывает, что учитываются
только те решения, для которых
значения всех переменных - целые. С точностью до
полиномиальных сводимостей задача разрешимости системы (4)
эквивалентна задаче ЦЛП. Доказательство этого оставляется читателю в
качестве упражнения.
Теорема 3.
Задача
проверки разрешимости системы линейных уравнений в
неотрицательных целых числах
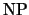 -полна. -полна.
Как
и в предыдущих случаях, нам необходимо доказать два утверждения: что
эта задача принадлежит классу
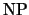 и что к ней сводятся все задачи из и что к ней сводятся все задачи из
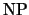 . Но теперь нетривиальны оба утверждения. Естественно пытаться
доказывать принадлежность . Но теперь нетривиальны оба утверждения. Естественно пытаться
доказывать принадлежность
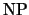 следующим образом: пусть Советник
сообщит решение, а Исполнитель его проверит. Но тогда решение должно
состоять из не слишком больших чисел, чтобы
Исполнитель мог проверить выполнение равенств (4)
за полиномиальное время. следующим образом: пусть Советник
сообщит решение, а Исполнитель его проверит. Но тогда решение должно
состоять из не слишком больших чисел, чтобы
Исполнитель мог проверить выполнение равенств (4)
за полиномиальное время.
Оказывается, что так оно и есть: из разрешимости системы (4)
следует существование не слишком длинных решений. Опишем кратко идею
доказательства.
Основная используемая оценка - это оценка величины определителя
матрицы через длину ее описания. Обозначим длину записи матрицы 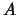 (кодировка указана в примере 1)
через
(кодировка указана в примере 1)
через 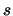 . Тогда . Тогда
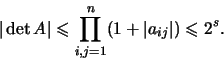 |
(10) |
Первое
неравенство следует непосредственно из определения 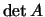 , второе -
из того, что запись числа , второе -
из того, что запись числа 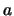 требует не менее требует не менее
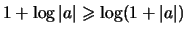 битов. битов.
Множество вещественных решений системы (4) является
полиэдром - пересечением конечного числа
полупространств.
Хорошо известная теорема выпуклой геометрии утверждает, что
любая точка полиэдра является выпуклой комбинацией его крайних точек и
точек на его крайних лучах. Крайние точки полиэдра, задаваемого
системой (4), являются решениями систем линейных уравнений вида
![\begin{displaymath}
\left\{
\begin{aligned}
Ax&=b, [3pt]
x_i&=0, \quad i\in S,
\end{aligned}\right.
\end{displaymath}](http://images.nature.web.ru/nature/2001/03/14/0001161983/img196.gif) |
(11) |
для каких-то подмножеств
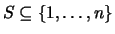 .
Координаты этих точек по правилу Крамера являются отношениями
миноров расширенной матрицы этой системы.
В силу
оценки (10) они не превосходят .
Координаты этих точек по правилу Крамера являются отношениями
миноров расширенной матрицы этой системы.
В силу
оценки (10) они не превосходят 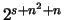 (в показателе
написана максимально возможная длина описания минора расширенной
матрицы). (в показателе
написана максимально возможная длина описания минора расширенной
матрицы).
Направляющие векторы крайних лучей - ненулевые (без
ограничения общности, целочисленные) решения однородных систем вида
![\begin{displaymath}
\left\{
\begin{aligned}
Ax&=0,\\
x_i&=0, \quad i\in S, [3pt]
\end{aligned}\right.
\end{displaymath}](http://images.nature.web.ru/nature/2001/03/14/0001161983/img199.gif) |
(12) |
поэтому можно считать, что для их координат выполняются те же
неравенства.
Обозначим крайние точки полиэдра
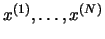 ,
направляющие векторы крайних лучей ,
направляющие векторы крайних лучей
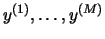 .
Пусть у системы (4) есть целочисленное решение .
Пусть у системы (4) есть целочисленное решение 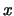 . Тогда
его можно записать в виде . Тогда
его можно записать в виде
 |
(13) |
где
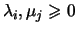 , ,
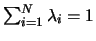 , все
координаты вектора , все
координаты вектора 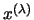 ограничены ограничены 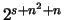 , а вектор , а вектор
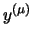 - целочисленный. Но тогда и вектор - целочисленный. Но тогда и вектор 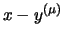 является
целочисленным решением системы (4), а его координаты не
превосходят является
целочисленным решением системы (4), а его координаты не
превосходят
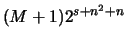 . Заметим, что . Заметим, что 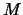 заведомо не
превосходит заведомо не
превосходит  (а если вспомнить теорему Каратеодори, то (а если вспомнить теорему Каратеодори, то 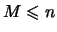 ). ).
Итак, мы доказали, что для разрешимой в неотрицательных целых числах
системы найдется и такое решение, длина записи которого 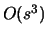 (мы
грубо оценили (мы
грубо оценили 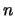 как как 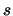 ). Отсюда следует принадлежность этой задачи
классу ). Отсюда следует принадлежность этой задачи
классу
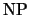 . .
Для доказательства
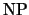 -полноты задачи разрешимости системы линейных
уравнений в неотрицательных целых числах сведем к ней задачу
3-КНФ. Построим по 3-КНФ систему линейных уравнений в
неотрицательных целых числах.
Булевой переменной -полноты задачи разрешимости системы линейных
уравнений в неотрицательных целых числах сведем к ней задачу
3-КНФ. Построим по 3-КНФ систему линейных уравнений в
неотрицательных целых числах.
Булевой переменной  из 3-КНФ сопоставим целочисленную
неотрицательную переменную из 3-КНФ сопоставим целочисленную
неотрицательную переменную 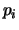 , отрицанию переменной , отрицанию переменной  - - 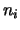 ,
дизъюнкции ,
дизъюнкции 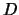 - переменную - переменную 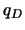 . Каждой дизъюнкции . Каждой дизъюнкции
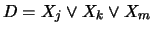 ( (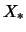 - литералы) сопоставим также уравнение - литералы) сопоставим также уравнение
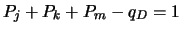 , в котором , в котором 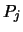 , , 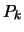 , , 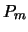 - переменные,
сопоставленные литералам дизъюнкции. - переменные,
сопоставленные литералам дизъюнкции.
Искомая система содержит для всех 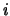 уравнения уравнения 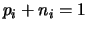 ,
а также все уравнения, сопоставленные дизъюнкциям из КНФ.
Очевидно, что выполнимость 3-КНФ равносильна совместности такой
системы. ,
а также все уравнения, сопоставленные дизъюнкциям из КНФ.
Очевидно, что выполнимость 3-КНФ равносильна совместности такой
системы.
Next: 6.4. 3-раскраска
Up: 6. Примеры NP-полных задач
Previous: 6.2. Разрешимость системы уравнений
Contents: Содержание
Написать комментарий
| 
