Next: 5. Набросок доказательства теоремы
Up: 4. Как различать сложные
Previous: 4.1. Полиномиальная сводимость
Contents: Содержание
Прежде всего заметим, что этот класс включает в себя только
характеристические функции
(напомним, что
задачи, соответствующие таким функциям, состоят в проверке некоторого
свойства входного слова).
Теперь дадим неформальное описание этого класса задач. У нас появляется
новый персонаж - Советник. От Исполнителя Советник отличается двумя
чертами: он интеллектуально всемогущ и пристрастен
(это означает, что Советник хочет, чтобы у рассматриваемого объекта
было признано наличие исследуемого свойства, безотносительно к
истинному положению дел). Последняя особенность не позволяет
Исполнителю слепо опираться на мнение
Советника: оно всегда одинаково. Исполнитель может задавать Советнику
вопросы и действовать, исходя из полученных ответов. Каждый
вопрос-ответ считается одним действием. Решение о значении функции
принимает Исполнитель.
Замечание 1.
В литературе по теории сложности Исполнитель (несколько более
сильный - снабженный монеткой для подбрасывания) именуется
Артуром, а Советник - Мерлином.
Функция (характеристическая)  принадлежит классу принадлежит классу
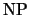 , если
существует алгоритм для пары (Исполнитель, Советник), который всегда
(при любых возможных вариантах диалога между Исполнителем и Советником)
заканчивается за полиномиальное от длины входа время и результат работы
которого удовлетворяет
следующему условию: если , если
существует алгоритм для пары (Исполнитель, Советник), который всегда
(при любых возможных вариантах диалога между Исполнителем и Советником)
заканчивается за полиномиальное от длины входа время и результат работы
которого удовлетворяет
следующему условию: если
 , то существует такой вариант диалога между Исполнителем и
Советником, что результат равен 1; если же , то существует такой вариант диалога между Исполнителем и
Советником, что результат равен 1; если же  , то при любом
варианте диалога результат равен 0. , то при любом
варианте диалога результат равен 0.
Замечание 2.
Из данного выше неформального определения ясно, что
 (Исполнитель может ничего не спрашивать).
Является ли это включение строгим? Довольно интенсивные, хотя и
безуспешные, попытки ответить на этот вопрос продолжаются уже почти
30 лет. С. Смейл включил проблему
(Исполнитель может ничего не спрашивать).
Является ли это включение строгим? Довольно интенсивные, хотя и
безуспешные, попытки ответить на этот вопрос продолжаются уже почти
30 лет. С. Смейл включил проблему
 в число трех
важнейших математических проблем следующего столетия (две другие -
гипотеза Римана и гипотеза Пуанкаре), см. [10]. в число трех
важнейших математических проблем следующего столетия (две другие -
гипотеза Римана и гипотеза Пуанкаре), см. [10].
Прежде чем давать формальное определение класса
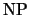 , заметим
следующее. Исполнитель работает вполне определенным образом, а
Советник - всеведущ. Поэтому, посмотрев на вход, Советник может сразу
сообщить Исполнителю весь их диалог, а Исполнитель - убедиться, что
Советник не соврал; Исполнителю на это потребуется время, полиномиально
зависящее от длины диалога. , заметим
следующее. Исполнитель работает вполне определенным образом, а
Советник - всеведущ. Поэтому, посмотрев на вход, Советник может сразу
сообщить Исполнителю весь их диалог, а Исполнитель - убедиться, что
Советник не соврал; Исполнителю на это потребуется время, полиномиально
зависящее от длины диалога.
Определение 5.
Функция 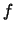 (со значениями в
множестве (со значениями в
множестве  ) принадлежит классу ) принадлежит классу
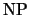 , если она представима в
форме , если она представима в
форме

где
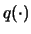 - полином, - полином,
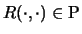 , а , а  - длина слова. - длина слова.
Здесь (и всюду далее) мы отождествляем логические значения
"ложь" и "истина" с 0 и 1 соответственно.
В духе предыдущего неформального обсуждения это определение нужно
понимать так:  - это сообщение Советника Исполнителю, а - это сообщение Советника Исполнителю, а
 - алгоритм проверки, который осуществляет
Исполнитель. - алгоритм проверки, который осуществляет
Исполнитель.
Замечание 3.
Приведем еще несколько неформальных интерпретаций класса
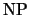 .
Слово .
Слово  в данном выше определении можно понимать как
"подсказку" Исполнителю, воспользовавшись которой он
может проверить выполнение в данном выше определении можно понимать как
"подсказку" Исполнителю, воспользовавшись которой он
может проверить выполнение
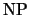 -свойства. Другими словами, у -свойства. Другими словами, у
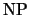 -задачи
есть ответ, который, быть может, трудно найти, но
проверить правильность ответа - легко. Популярно также представление
о слове -задачи
есть ответ, который, быть может, трудно найти, но
проверить правильность ответа - легко. Популярно также представление
о слове  как о "доказательстве наличия свойства"
(подразумевается, что изучение доказательства занимает полиномиальное
от его длины время). как о "доказательстве наличия свойства"
(подразумевается, что изучение доказательства занимает полиномиальное
от его длины время).
Лемма 1.
Пусть
 . Тогда
а) . Тогда
а)
 ;
б) ;
б)
 . .
Доказательство.
Пункт а) фактически доказан выше.
Докажем пункт б), привлекая неформальных персонажей из предыдущего
обсуждения. Советник сообщает Исполнителю  (длина которого
ограничена некоторым полиномом (длина которого
ограничена некоторым полиномом  от длины от длины 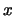 , поскольку , поскольку  ) и
слово ) и
слово  , которое убеждает Исполнителя в том, что , которое убеждает Исполнителя в том, что  .
Исполнитель может проверить, что ему действительно сообщено .
Исполнитель может проверить, что ему действительно сообщено
 . .

Определение 6.
Функция
 называется называется
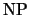 -полной, если любая
функция из -полной, если любая
функция из
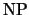 к ней сводится4. к ней сводится4.
Если некоторую
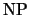 -полную функцию -полную функцию 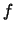 можно вычислять
за время можно вычислять
за время  , то любую функцию , то любую функцию  из из
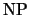 можно вычислять за время можно вычислять за время
 , где число , где число  зависит от зависит от  , но не от входа. , но не от входа.
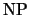 -полные функции существуют, например, функция задающая предикат
выполнимость для булевых формул: -полные функции существуют, например, функция задающая предикат
выполнимость для булевых формул:

В первой строчке предполагается, что 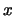 есть запись логической
формулы с булевыми переменными есть запись логической
формулы с булевыми переменными
 и
пропозициональными связками и
пропозициональными связками
 . .
Теорема 1. (Кук, Левин)
1)
 ;
2) ;
2)  - -
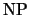 -полна. -полна.
Следствие .
Если  , то , то
 . .
Эскиз доказательства теоремы Кука-Левина будет приведен в следующем
разделе.
А пока заметим, что большая часть доказательств
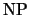 -полноты
использует полиномиальную сводимость и следующую лемму. -полноты
использует полиномиальную сводимость и следующую лемму.
Лемма 2.
Если  и и
 , то , то  - -
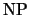 -полная.
И вообще, если -полная.
И вообще, если  - -
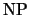 -полная, -полная,
 и и
 , то , то  - -
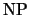 -полная. -полная.
Доказательство.
Достаточно проверить транзитивность
сводимости: если
 , ,
 , то , то
 . Она следует из того, что композиция
двух полиномиально вычислимых функций полиномиально вычислима. . Она следует из того, что композиция
двух полиномиально вычислимых функций полиномиально вычислима.

Next: 5. Набросок доказательства теоремы
Up: 4. Как различать сложные
Previous: 4.1. Полиномиальная сводимость
Contents: Содержание
Написать комментарий
| 
