Покажем, что спектр и собственные векторы гамильтониана ГО можно найти, используя только алгебру наблюдаемых и общие свойства гильбертова пространства состояний.
Запишем гамильтониан в виде
где, как и выше, 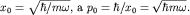 Нормированный (безразмерный) гамильтониан Нормированный (безразмерный) гамильтониан 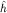 представим в факторизованном виде: представим в факторизованном виде:
Введем эрмитово сопряженные друг другу операторы
где учтен фундаментальный коммутатор ![$[\hat x,\hat p_x]=i\hbar$](http://images.nature.web.ru/nature/2001/02/21/0001161226/tex/formula740.gif) и равенство и равенство 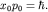 В результате получаем факторизованное представление гамильтониана ГО:
В результате получаем факторизованное представление гамильтониана ГО:
Задача свелась к нахождению спектра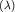 и нормированных собственных векторов (СВ) и нормированных собственных векторов (СВ)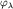 эрмитова оператора эрмитова оператора
Итак,
Отсюда получаем:
Следовательно, спектр энергии ГО ограничен снизу:
Итак, 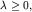 причем наименьшему собственному значению причем наименьшему собственному значению 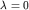 отвечает вектор отвечает вектор 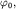 удовлетворяющий уравнению удовлетворяющий уравнению
Далее заметим, что
или
Используя этот коммутатор, получаем
откуда
Следовательно,
Получаем нормированный СВ
Подействовав k раз оператором  на вектор на вектор 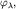 получим нормированный СВ получим нормированный СВ
Мы уже доказали, что 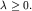 Поэтому процедура должна оборваться при достижении СВ Поэтому процедура должна оборваться при достижении СВ 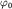 . Это возможно только при . Это возможно только при
В результате мы получили спектр энергии ГО:
Покажем теперь, что все СВ могут быть построены по вектору 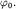 Воспользуемся коммутатором Воспользуемся коммутатором
Имеем
Значит,
Далее,
В итоге получим:
Применим полученные формулы в координатном представлении для вывода явных выражений для волновых функций ГО. Имеем
Для определения волновой функции основного состояния получаем простое уравнение
Его решение
Нормировочный коэффициент определяем из условия
откуда (выбирая соответствующий фазовый множитель)
Волновую функцию состояния с номером n>0 находим по общей формуле:
Далее воспользуемся легко проверяемым операторным тождеством:
откуда
В результате получим волновые функции осциллятора в окончательном виде:
Состояния, минимизирующие произведение неопределенностей координаты и импульса частицы, подчиняются, как показано в п. 4, уравнению
Для осциллятора оно может быть, очевидно, записано в виде:
где  - произвольное комплексное число. Итак, минимизирующие СН состояния описываются собственными векторами оператора - произвольное комплексное число. Итак, минимизирующие СН состояния описываются собственными векторами оператора 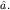 Комплексность собственных значений объясняется неэрмитовостью Комплексность собственных значений объясняется неэрмитовостью 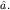
Найдем выражение для 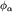 в базисе из СВ гамильтониана (энергетическое представление). Имеем в базисе из СВ гамильтониана (энергетическое представление). Имеем
откуда следует рекуррентное соотношение для коэффициентов:
Коэффициент c0, полагая его действительным, находим из нормировочного условия:
где учтено условие ортонормированности 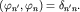
Итак,
Следовательно, вероятность обнаружить осциллятор в стационарном состоянии с энергией En равна
Мы получили известное распределение Пуассона, так что физический смысл параметра 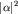 таков: таков:
До сих пор мы рассматривали состояние осциллятора 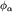 в фиксированный момент времени t=0. Состояние в фиксированный момент времени t=0. Состояние 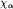 при t>0 получим очевидной заменой базисных векторов в разложении при t>0 получим очевидной заменой базисных векторов в разложении 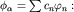
Учтя выражения для спектра, 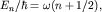 получим закон эволюции во времени минимизирующего состояния: получим закон эволюции во времени минимизирующего состояния:
Отсюда следует, что 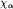 , как и , как и 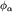 , также собственный вектор оператора , также собственный вектор оператора  : :
Вычислим среднее значение координаты осциллятора в состоянии 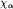 , Удобно использовать представление , Удобно использовать представление
Тогда получим
или, полагая 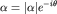 , ,
Таким образом, среднее значение координаты в состоянии 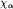 изменяется по классическому закону изменяется по классическому закону
Найдем явный вид 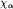 , решая уравнение , решая уравнение 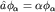 в координатном представлении: в координатном представлении:
В результате получим нормированное решение
представляющее собой нерасплывающийся волновой пакет. Впервые он был построен Шредингером в 1926 г. Координаты в состоянии 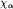 распределены по нормальному закону: распределены по нормальному закону:
Центр пакета движется по классическому закону, ширина пакета не зависит от времени:
Как уже было показано выше, энергия в пакете распределена по закону Пуассона:
Независимость распределения от времени обусловлена тем, что гамильтониан осциллятора - интеграл движения. Средняя энергия может быть выражена через амплитуду колебаний около центра пакета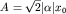 : :
Эта формула отличается от классической добавлением в правой части энергии основного состояния осциллятора 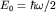 (см. выше), которой можно пренебречь только при (см. выше), которой можно пренебречь только при 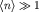 (при этом распределение Пуассона переходит, как известно, в нормальное распределение Гаусса). (при этом распределение Пуассона переходит, как известно, в нормальное распределение Гаусса).
Заметим, что теоремы Эренфеста для ГО дают классические уравнения движения для средних:
откуда
Это объясняется квадратичной зависимостью потенциала ГО от координаты.
Итак, мы построили нерасплывающиеся волновые пакеты 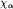 , минимизирующие соотношение неопределенностей "координата - импульс". Они описывают состояния ГО, максимально близкие к классическим. Эти состояния называют когерентными состояниями, так как они используются для описания когерентных свойств электромагнитного излучения в квантовой теории поля
(R. Glauber, 1963): можно показать, что свободное электромагнитное поле эквивалентно бесконечному набору независимых гармонических осцилляторов. , минимизирующие соотношение неопределенностей "координата - импульс". Они описывают состояния ГО, максимально близкие к классическим. Эти состояния называют когерентными состояниями, так как они используются для описания когерентных свойств электромагнитного излучения в квантовой теории поля
(R. Glauber, 1963): можно показать, что свободное электромагнитное поле эквивалентно бесконечному набору независимых гармонических осцилляторов.
Назад | Вперед
Посмотреть комментарии[1]
|

