Пусть  - произвольное состояние, эволюционирующее во времени согласно уравнению Шредингера - произвольное состояние, эволюционирующее во времени согласно уравнению Шредингера
Получим уравнение для изменения среднего значения наблюдаемой 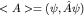 в этом состоянии. Имеем в этом состоянии. Имеем
Здесь учтена эрмитовость 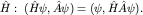 Итак,
Итак,
Это уравнение - квантовый аналог классического уравнения для динамической переменной A(q,p,t):
где введена скобка Пуассона
Таким образом, при переходе к квантовой теории
Заметим, что алгебраические свойства скобки Пуассона совпадают со свойствами коммутатора наблюдаемых.
Определим оператор производной по времени:
Тогда
Пусть наблюдаемая 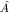 явно не зависит от времени и коммутирует с гамильтонианом: явно не зависит от времени и коммутирует с гамильтонианом:
Тогда в любом состоянии  среднее значение наблюдаемой <A>=const. В этом случае среднее значение наблюдаемой <A>=const. В этом случае 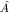 называется интегралом квантовых уравнений движения.
Рассмотрим важный частный случай независящего от времени гамильтониана: называется интегралом квантовых уравнений движения.
Рассмотрим важный частный случай независящего от времени гамильтониана:
В этом случае существуют специальные решения уравнения Шредингера, которые легко получаются методом разделения переменных:
где 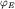 не зависят от времени и являются (как и не зависят от времени и являются (как и 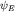 ) собственными векторами гамильтониана: ) собственными векторами гамильтониана:
Собственные значения E являются допустимыми значениями энергии системы, так как гамильтониан - оператор энергии, соответствующий классической функции Гамильтона.
Состояния 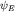 называются стационарными состояниями. Их основные свойства таковы:
плотность вероятности и поток вероятности в этих состояниях не зависят от времени: называются стационарными состояниями. Их основные свойства таковы:
плотность вероятности и поток вероятности в этих состояниях не зависят от времени:
Средние значения наблюдаемых не зависят от времени:
Вероятность обнаружить собственное значение 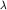 наблюдаемой наблюдаемой 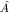 не зависит от времени: не зависит от времени:
Произвольное (нестационарное) состояние может быть разложено по стационарным состояниям - собственным векторам гамильтониана:
В нестационарном состоянии энергия не имеет определенного значения, но среднее значение ее от времени не зависит:
так как 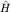 - интеграл движения: - интеграл движения:
Если наблюдаемая 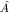 не коммутирует с гамильтонианом, то ее среднее, как и должно быть, зависит от времени (даже при не коммутирует с гамильтонианом, то ее среднее, как и должно быть, зависит от времени (даже при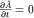 ): ):
Присутствие здесь недиагональных матричных элементов оператора наблюдаемой 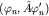 отражает характерный квантовомеханический эффект интерференции различных стационарных состояний. отражает характерный квантовомеханический эффект интерференции различных стационарных состояний.
Легко проверить, что в нестационарном состоянии  и j также зависят от времени.
Рассмотрим подробнее случай одномерного движения частицы в поле U(x). Гамильтониан и j также зависят от времени.
Рассмотрим подробнее случай одномерного движения частицы в поле U(x). Гамильтониан
Учитывая фундаментальный коммутатор ![$[\hat x,\hat p_x]=i\hbar$](http://images.nature.web.ru/nature/2001/02/21/0001161226/tex/formula740.gif) , вычислим по общему правилу (см. выше) оператор скорости: , вычислим по общему правилу (см. выше) оператор скорости:
В результате
Далее
Последний коммутатор проще всего вычислить в координатном представлении:
В результате получим:
Отсюда для средних значений следуют уравнения, впервые полученные Эренфестом (P. Ehrenfest) в 1927 г.:
Это, очевидно, квантовый аналог системы канонических уравнений Гамильтона. Отсюда следует квантовое обобщение закона Ньютона:
Эти уравнения выражают содержание теорем Эренфеста.
Рассмотрим переход к классическим уравнениям движения. Пусть состояние  представляет собой волновой пакет, сосредоточенный в окрестности точки x=<x>. Разложив силу представляет собой волновой пакет, сосредоточенный в окрестности точки x=<x>. Разложив силу 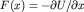 в ряд по в ряд по 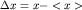 и усреднив по пакету, получим с точностью до членов второго порядка малости уравнение движения и усреднив по пакету, получим с точностью до членов второго порядка малости уравнение движения
Здесь учтено, что 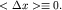 При условии При условии
движение центра волнового пакета описывается классическим уравнением Ньютона. Этого условия, однако, недостаточно. Надо учесть соотношение неопределенностей
и потребовать относительной малости флуктуаций импульса около среднего значения <px>: 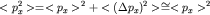 при при
В этом приближении получаем классическую функцию Гамильтона:
и можно говорить о движении центра пакета по траектории.
Указанные два условия одновременно выполняются при движении частицы с относительно большим импульсом в плавно меняющемся внешнем поле.
Вернемся к интегралам движения в квантовой механике и покажем, что их существование связано с симметрией системы. Ограничимся случаем 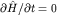 . Пусть спектр гамильтониана инвариантен относительно некоторых преобразований векторов состояний: . Пусть спектр гамильтониана инвариантен относительно некоторых преобразований векторов состояний:
где 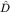 - линейный оператор. Инвариантность означает, что из уравнения - линейный оператор. Инвариантность означает, что из уравнения
следует такое же уравнение для преобразованного вектора:
Отсюда получаем условие инвариантности гамильтониана:
Естественно потребовать также сохранения нормы вектора:
Следовательно, оператор преобразования должен быть унитарным:
Для приложений представляют интерес унитарные операторы вида
где 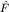 - эрмитов оператор - эрмитов оператор 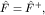 т.е. некоторая наблюдаемая; т.е. некоторая наблюдаемая;  - вещественный параметр. Условие инвариантности гамильтониана принимает вид - вещественный параметр. Условие инвариантности гамильтониана принимает вид
Поэтому наблюдаемая 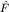 - интеграл движения (при - интеграл движения (при 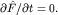 ) )
Пример. Пусть свойства системы инвариантны относительно группы G линейных непрерывных преобразований g координат:
Ввиду скалярности волновой функции ее закон преобразования имеет вид:
Линейные операторы 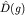 реализуют представление группы G. реализуют представление группы G.
Рассмотрим группу трансляций:
r'=r+a,
где a- постоянный вектор.
Тогда
или
где 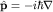 - оператор импульса, который оказывается генератором группы трансляций в пространстве волновых функций. Для свободной частицы - оператор импульса, который оказывается генератором группы трансляций в пространстве волновых функций. Для свободной частицы 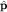 коммутирует с гамильтонианом коммутирует с гамильтонианом 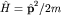 , т.е. является интегралом движения. , т.е. является интегралом движения.
Рассмотрим группу вращений SO(3). Нетрудно показать, что волновая функция преобразуется при вращениях по закону:
где  - угол поворота вокруг оси, направление которой задано единичным вектором n; - угол поворота вокруг оси, направление которой задано единичным вектором n;
- оператор момента импульса, или угловой момент. Следовательно, оператор момента - генератор группы вращений. Можно показать (см. ниже п. 9), что для частицы, движущейся в центрально-симметричном поле U(|r|), момент - интеграл движения:
.
Положим в общей формуле СН
С учетом соотношения
получаем
Введем характерное время изменения наблюдаемой :
Тогда получим
где 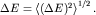 Следовательно, множество значений Следовательно, множество значений 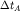 для всевозможных наблюдаемых ограничено снизу. Определим время, за которое в процессе эволюции системы заметно изменяется распределение хотя бы одной из наблюдаемых: для всевозможных наблюдаемых ограничено снизу. Определим время, за которое в процессе эволюции системы заметно изменяется распределение хотя бы одной из наблюдаемых:
.
Тогда получаем, что для любого состояния  справедливо соотношение, называемое соотношением неопределенностей "время - энергия": справедливо соотношение, называемое соотношением неопределенностей "время - энергия":
Подчеркнем, что здесь  - неопределенность энергии в состоянии - неопределенность энергии в состоянии 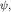 которая от времени не зависит (в силу которая от времени не зависит (в силу 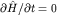 ). ).
Качественно СН "время - энергия" может быть получено из анализа эволюции волнового пакета, рассмотренного выше в п. 2: разброс частот в пакете и характерное время его расплывания связаны условием 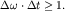 Учитывая, что Учитывая, что 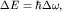 получим получим 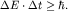
Назад | Вперед
Посмотреть комментарии[1]
|

