Зная плотность вероятности координаты частицы, можно найти среднее значение координаты - математическое ожидание:
Как найти среднее значение импульса <p>? Рассмотрим волновой пакет:
Здесь время t фиксировано и явно не указано в качестве одного из аргументов волновой функции (ВФ). Преобразуем условие нормировки ВФ:
Здесь использовано известное соотношение:
Естественно, следуя Борну, интерпретировать |C(k)|2 как плотность вероятности обнаружить при измерении импульс частицы 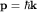 . Фурье-образ C(k) функции . Фурье-образ C(k) функции  называется волновой функцией в импульсном представлении. Ясно, что тогда среднее значение импульса называется волновой функцией в импульсном представлении. Ясно, что тогда среднее значение импульса
Проинтегрировав в последнем интеграле по частям в предположении, что 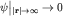 , получим с учетом , получим с учетом
выражение для среднего импульса в координатном представлении:
Итак, в пространстве волновых функций импульсу соответствует дифференциальный оператор:
.
Координате отвечает оператор умножения:
Заметим, что в пространстве волновых функций в импульсном представлении C(p) имеем:
Поэтому, в частности, средняя координата
Полученные результаты обобщаются следующим образом: каждой физической величине A, значение которой может быть в принципе измерено, -наблюдаемой однозначно соответствует линейный оператор 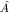 в пространстве волновых функций. в пространстве волновых функций.
Фундаментальный оператор Гамильтона - гамильтониан, определяющий эволюцию волновой функции, выражается через операторы координаты и импульса:
Среднее значение наблюдаемой вычисляется по правилу:
В дальнейшем будем использовать обозначения из функционального анализа, предполагая, что множество волновых функций - линейное пространство. Скалярное произведение:
Норма 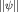 вектора вектора 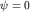 определена в виде определена в виде
причем 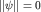 тогда и только тогда, когда тогда и только тогда, когда 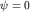 . .
Оператору 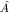 ставится в соответствие эрмитово сопряженный оператор ставится в соответствие эрмитово сопряженный оператор 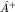 согласно определению: согласно определению:
.
Пусть 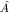 - оператор наблюдаемой A. Ее среднее значение должно быть действительным числом. Поэтому - оператор наблюдаемой A. Ее среднее значение должно быть действительным числом. Поэтому
Следовательно, оператор наблюдаемой должен быть эрмитовым: 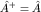 . Легко проверить, что уже введенные операторы координаты и импульса эрмитовы в пространстве квадратично интегрируемых функций. . Легко проверить, что уже введенные операторы координаты и импульса эрмитовы в пространстве квадратично интегрируемых функций.
Линейность уравнения Шредингера и операторов наблюдаемых обеспечивает выполнение фундаментального принципа суперпозиции, согласно которому:
Если квантовая система может находиться в состояниях, описываемых волновыми функциями 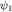 и и 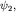 то она может также находиться и в состоянии то она может также находиться и в состоянии
где c1,c2- произвольные комплексные числа.
Функции  и и 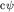 , где с - произвольное комплексное число, описывают одно и то же состояние. , где с - произвольное комплексное число, описывают одно и то же состояние.
Для физически реализуемых состояний  . Принцип суперпозиции (см. п. 2) всегда позволяет выбрать для таких состояний условие нормировки . Принцип суперпозиции (см. п. 2) всегда позволяет выбрать для таких состояний условие нормировки 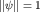 . Рассмотрим состояние . Рассмотрим состояние 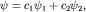 , представляющее собой суперпозицию состояний , представляющее собой суперпозицию состояний 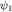 и и 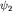 . Для плотности вероятности, квадрата нормы и среднего значения наблюдаемой A в этом состоянии получаем соответственно выражения: . Для плотности вероятности, квадрата нормы и среднего значения наблюдаемой A в этом состоянии получаем соответственно выражения:
Отсюда видно, что квантовая механика не сводится к классической теории вероятности: возникает характерный эффект интерференции состояний 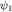 и и 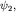 не имеющий классического аналога.
Как мы уже видели, предсказания квантовой теории носят вероятностный характер. Выясним, когда измерение наблюдаемой A дает определенный результат. Рассмотрим отклонение от среднего не имеющий классического аналога.
Как мы уже видели, предсказания квантовой теории носят вероятностный характер. Выясним, когда измерение наблюдаемой A дает определенный результат. Рассмотрим отклонение от среднего 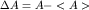 . Ему отвечает наблюдаемая . Ему отвечает наблюдаемая 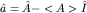 , где , где 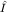 - единичный оператор (в дальнейшем его будем опускать). Дисперсия случайной переменной A в состоянии - единичный оператор (в дальнейшем его будем опускать). Дисперсия случайной переменной A в состоянии  равна равна
Она обращается в нуль только при 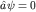 , или , или
Следовательно, в указанном состоянии наблюдаемая имеет определенное значение, которое совпадает с одним из собственных значений оператора наблюдаемой. Само состояние описывается волновой функцией, представляющей собой собственный вектор оператора.
В дальнейшем для краткости, если это не приведет к недоразумению, мы будем отождествлять понятия состояния и соответствующей ему волновой функции (используется также термин вектор состояния), наблюдаемой и оператора наблюдаемой.
Пусть наблюдаемая 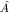 имеет дискретный спектр: имеет дискретный спектр:
причем система собственных функций 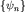 полна и ортонормированна, т.е. образует базис в пространстве состояний: полна и ортонормированна, т.е. образует базис в пространстве состояний:
Здесь  - произвольный вектор с единичной нормой. Имеем следующие соотношения: - произвольный вектор с единичной нормой. Имеем следующие соотношения:
Отсюда следует, что
есть вероятность получить значение An наблюдаемой A при измерении в состоянии  , причем значений , причем значений 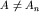 на опыте обнаружить нельзя. на опыте обнаружить нельзя.
Если наблюдаемая 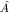 имеет непрерывный спектр имеет непрерывный спектр 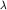 , то , то
Тогда
- плотность вероятности, т.е. 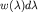 - вероятность обнаружить значение A в интервале - вероятность обнаружить значение A в интервале 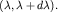 При этом При этом
Условие ортонормированности заменяется условием нормировки на  -функцию: -функцию:
Пример. Собственные векторы оператора импульса 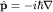 имеют вид имеют вид
Для оператора координаты 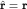 имеем имеем
В общем случае смешанного спектра получаем
Условие полноты системы собственных функций имеет вид:
Рассмотрим условия, при которых две наблюдаемых A и B могут быть одновременно измерены. Пусть в некотором состоянии они имеют определенные значения. Тогда, как мы уже знаем, вектор состояния должен быть собственным для операторов 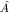 и и 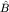 : :
Предположим, что 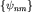 образуют полную систему собственных векторов. Тогда для произвольного вектора состояния образуют полную систему собственных векторов. Тогда для произвольного вектора состояния
имеем
Ввиду произвольности  получаем операторное равенство получаем операторное равенство
т.е. наблюдаемые должны коммутировать.
Это утверждение обобщается на случай произвольного (смешанного) спектра и представляет собой известную теорему из функционального анализа: если два оператора имеют общий полную систему собственных векторов, то они коммутируют. Справедлива и обратная теорема: если ![$[\hat A,\hat B]=0,$](http://images.nature.web.ru/nature/2001/02/21/0001161226/tex/formula660.gif) то операторы то операторы 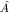 и и 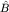 и имеют общую систему собственных функций. и имеют общую систему собственных функций.
Определим полный набор коммутирующих наблюдаемых  :
операторы :
операторы 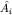 попарно коммутируют, попарно коммутируют, ![$[\hat A_i,\hat A_j]=0;\; i,j=\overline{1,n};$](http://images.nature.web.ru/nature/2001/02/21/0001161226/tex/formula664.gif) ни один из операторов
ни один из операторов 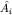 не является функцией от остальных;
любой оператор, коммутирующий со всеми не является функцией от остальных;
любой оператор, коммутирующий со всеми 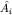 , есть функция от этих операторов. , есть функция от этих операторов.
Из изложенного выше следует,что существует общая полная система
собственных векторов полного набора наблюдаемых:
Поэтому произвольный вектор состояния может быть представлен в виде
причем 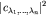 есть вероятность получить в результате одновременного измерения наблюдаемых есть вероятность получить в результате одновременного измерения наблюдаемых  значения значения  . .
Таким образом, состояние системы в квантовой механике можно задать полным набором значений наблюдаемых. Их число называется числом степеней свободы системы. В общем случае оно определяется из опыта. В частных случаях это число совпадает с числом степеней свободы соответствующей классической системы.
Полный набор наблюдаемых может быть задан многими способами. Его фиксация определяет некоторое представление пространства состояний квантовой системы функциями
определенными на спектре операторов  . Функция . Функция  называется волновой функцией системы в данном представлении. называется волновой функцией системы в данном представлении.
Пример. Для точечной (бесструктурной) частицы полный набор наблюдаемых образуют операторы координат 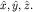 Ему отвечает координатное представление волновых функций: Ему отвечает координатное представление волновых функций:
Другой полный набор составляют операторы компонент импульса 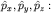
,
где 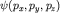 - волновая функция в импульсном представлении (выше она обозначалась C(p)). - волновая функция в импульсном представлении (выше она обозначалась C(p)).
Назад | Вперед
Посмотреть комментарии[1]
|

