Научная Сеть >> Основы квантовой механики

Наука >> Физика >> Теоретическая физика >> Квантовая механика | Курсы лекций

См. также

Проект Краткая Энциклопедия "Физика" (Вопросы и ответы): 1301

Открытие неклассической логики поведения квантовых объектов - одно из удивительных достижений современной физики: Об интерпретациях классической и квантовой теорий

Утро квантовой эры. Три четверти века назад появилось нестационарное уравнение Шредингера.

О лженауке, ее последствиях и об ошибках в науке

Зонная структура электронного энергетического спектра в твердых телах. Модели свободных и сильно связанных электронов.: ref2

75 лет волновой механике и стационарному уравнению Шредингера.

Наноэлектроника - основа информационных систем XXI века: Квантовые основы наноэлектроники

Открытие неклассической логики поведения квантовых объектов - одно из удивительных достижений современной физики: ref2

11 января - день рождения Д.И. Блохинцева

Векторное пространство

Квантовые ямы, нити, точки. Что это такое?: Классические и квантовые законы движения электронов

Первый в мире и в России журнал о квантовых компьютерах!

Горячие ядра и фазовый переход жидкость-газ в ядерном веществе: Введение

Новая ситуация в квантовой механике (о возможностях управления спектрами, рассеянием, распадами)

Соотношение неопределенностей или принцип дополнительности?

Мировая линия Гамова

Алгебраический подход в квантовой теории поля

Законы физики в космосе

Основы квантовой механики.

А.В. Борисов (Физический факультет МГУ)
Физический факультет МГУ, 1998 г.

Содержание

Уравнение Шредингера

Физические предпосылки создания квантовой механики

Атомные спектры излучения

Согласно экспериментальным данным, полученным к концу XIX века, частоты спектральных линий данного атома

$\omega_{nn'}=T(n)-T(n')$

где T(n)- функция целого числа (спектральный терм), n=1,2,3,... . Это соотношение выражает комбинационный принцип Ритца (W. Ritz). В частности, для спектра излучения атома водорода Бальмер (J. Balmer) в 1885 г. эмпирически нашел простую формулу

$\omega_{nn'}=R\left( \frac{1}{n'^2}-\frac{1}{n^2}\right),$

где R - постоянная Ридберга (J. Rydberg).
В классической теории для периодического движения заряженных частиц частоты излучения кратны основной частоте:

$\omega_{n}=n\omega_0, \; \omega_0=\frac{2\pi }{\tau},$

$\tau$ - период. Таким образом, эта теория не может объяснить комбинационный принцип.

Равновесие электромагнитного излучения и вещества

Рассмотрим замкнутый сосуд, нагретый до температуры T. Внутри него находится равновесное электромагнитное излучение: излучаемая и поглощаемая атомами вещества стенок сосуда в единицу времени энергии равны. Спектральная плотность энергии равновесного излучения - универсальная функция частоты и температуры 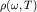$\rho(\omega,T)$ (не зависит от размеров и формы сосуда и вещества стенок). Из классической теории следует закон Рэлея (J. Rayleigh):

$\rho \sim \omega^2 T,$

т.е. полная плотность (энергия в единице объема)

$\int\limits_0^{\infty}d\omega\rho(\omega, T)=\infty,$

что означает невозможность равновесия в противоречии с экспериментом.
В 1900 г. Планк (M. Planck), анализируя механизм установления равновесия между веществом и излучением, выдвинул фундаментальную гипотезу квантования: вещество испускает энергию излучения конечными порциями (квантами), пропорциональными частоте излучения. Коэффициент пропорциональности - универсальная постоянная h, имеющая размерность механического действия. В простейшей модели вещества в виде атомных осцилляторов это означает, что энергия E осциллятора частоты $\omega$ квантуется по закону

$E_n=n\hbar \omega,\; n=0,1,2\ldots.$

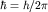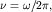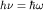Здесь введена постоянная Планка $\hbar=h/2\pi$ (сам Планк использовал вместо циклической частоты $\omega$ линейную частоту $\nu=\omega/2\pi,$ так что $h\nu=\hbar\omega$ ).
Используя гипотезу квантования (противоречащую классической физике!), Планку удалось получить следующую формулу для спектральной плотности энергии равновесного излучения:

$\rho(\omega,T)=\frac{\hbar\omega^3}{\pi^2 c^3 (e^{\hbar\omega/k_{B}T}-1)},$

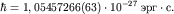
где скорость света c и постоянная Больцмана k_B(L. Boltzmann) известны из классической физики. Формула Планка прекрасно согласуется с экспериментом, позволяющим определить постоянную Планка (приводим современное значение): $\hbar=1,05457266(63)\cdot 10^{-27} \; эрг\cdot с.$

Фотоэффект

Планк приписал квантовые свойства атомным осцилляторам, а не излучению. В 1905 г. А. Эйнштейн (A. Einstein), развивая гипотезу Планка, сделал второй шаг: само электромагнитное излучение состоит из отдельных квантов - частиц, названных позже фотонами. Энергия фотона, отвечающего излучению частоты $\omega$ , равна

$\varepsilon=\hbar\omega.$

Гипотеза Эйнштейна возникла при анализе фотоэффекта, открытого Герцем в 1887 г. (H. Hertz) и подробно исследованного А.Г. Столетовым в 1888-90 г. Эффект состоит в испускании веществом электронов под действием падающего на вещество излучения достаточно высокой частоты. Объяснение законов фотоэффекта следует из выведенного Эйнштейном уравнения:

$\hbar\omega=\frac{mv^2}{2}+A,$

т.е. кинетическая энергия электрона - линейная функция частоты ( A - работа выхода, характерная для данного вещества) и не зависит от интенсивности излучения, что противоречит классической теории, но подтверждается экспериментом.

Эффект Комптона

В 1922 г. Комптон (A. Compton) обнаружил увеличение длины волны 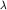$\lambda$ рентгеновского излучения вследствие его рассеяния электронами вещества. Согласно же классической теории длины волн падающего и рассеянного излучения должны совпадать. Теория эффекта была построена Комптоном и независимо Дебаем (P. Debye) на основе фотонной гипотезы Эйнштейна. Взаимодействие излучения с электроном сводится к упругому столкновению фотона с покоящимся электроном. При этом импульс фотона определяется в виде

${\bf p}=\hbar{\bf k}.$

Здесь волновой вектор

${\bf k}=\frac{\omega}{c}{\bf n},$

n - единичный вектор в направлении распространения монохроматической волны, соответствующей фотону. Это определение - следствие того, что величины

$k^{\mu}=\left( \frac{\omega}{c},{\bf k}\right)\; и \; p^\mu=\left( \frac{E}{c},{\bf p}\right)$

образуют 4-векторы относительно преобразований Лоренца (см. первую часть курса физики).
Запишем законы сохранения энергии и импульса для указанного процесса столкновения:

$\hbar +mc^2=\hbar\omega' +E,\; \hbar{\bf k}=\hbar{\bf k}'+{\bf p},$

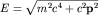где $E=\sqrt{m^2c^4+c^2{\bf p}^2}$ - энергия электрона после столкновения. Отсюда получаем частоту рассеянного фотона:

$\omega'=\frac{\omega}{1+\frac{\hbar\omega}{mc^2}(1-\cos\theta)},$

где $\theta$ - угол между k и k' (угол рассеяния). Учитывая связь частоты и длины волны

$\lambda=2\pi c/\omega,$

находим изменение длины волны при рассеянии:

$\Delta\lambda=\lambda'-\lambda=4\pi \lambda_e \sin^2\frac{\theta}{2}.$

Здесь введена комптоновская длина волны электрона

$\lambda_e=\frac{\hbar}{mc}=3,86\cdot 10^{-11} {\rm см}.$

Для рентгеновского излучения (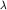 $\lambda$ ~10^-9см) получаем

$\frac{\Delta\lambda}{\lambda}\leq 4\pi \frac{\lambda_e}{\lambda}\sim 0,\! 1 ,$

т.е. вполне заметный эффект. Для видимого света (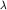 $\lambda$ ~10^-5см) эффект гораздо меньше (~10^-5). Найденная зависимость изменения длины волны от угла рассеяния прекрасно согласуется с экспериментом.

Назад | Вперед

MMOnline

Посмотреть комментарии[1]