Алгебра токов - система перестановочных соотношений между компонентами различных локальных токов в один и тот же момент
времени. В частности, для временных компонент SU(З)-октетов токов эта алгебра замкнута
(т. е. коммутатор токов выражается через сами токи):
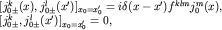 | (1) |
где
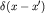
-
дельта-функция Дирака,
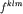
- т. н.
структурные константы группы
SU(3),
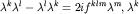
- матрицы Гелл-Мана, действующие в пространстве u-, d-, s-
кварков,
k,
l,
m - 1, 2, ..., 8, а значки

означают "плюс" и "минус" компоненты
векторных (
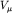
) и
аксиальных (
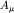
) токов:
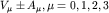
(используется система единиц
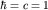
). В пределе
нулевой массы
пи-мезона токи
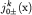
являются
плотностями сохраняющихся зарядов и алгебра токов описывает
киральную симметрию.
Аналогичные соотношения для пространственных компонент токов содержат в правой части производные от дельта-функции - т. н. швингеровские члены.
Перестановочные соотношения (1) имеют такой же вид, как и для токов, составленных из полей свободных кварков. В квантовой хромодинамике (КХД) это
объясняется свойством асимптотической свободы, на малых расстояниях эффективная константа связи (эффективный заряд) мала и сильным
взаимодействием можно пренебречь.
Алгебра токов сформулирована как эвристическое утверждение М. Гелл-Маном (М. Gell-Mann) в начале 1960-х гг. до появления современных кварковых теорий
(КХД, теории электрослабых взаимодействий). Она дала возможность получить ряд соотношений, допускающих непосредственное сравнение с опытом. Эти соотношения
носят характер правил сумм (т. е. предсказаний для интегралов от наблюдаемых сечений) или низкоэнергетических теорем,
т. е. предсказаний
для амплитуд процессов в пределе нулевых 4-импульсов одной или нескольких частиц. Используя дисперсионные соотношения
(см. Дисперсионных соотношений метод), значение амплитуды при нулевых 4-импульсах иногда (например, для 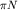 -рассеяния) удается переписать
в виде интеграла от сечений, так что одно и то же предсказание может фигурировать и как правило сумм, и как низкоэнергетическая теорема.
-рассеяния) удается переписать
в виде интеграла от сечений, так что одно и то же предсказание может фигурировать и как правило сумм, и как низкоэнергетическая теорема.
Одно из наиболее известных следствий алгебры токов - соотношение Адлера-Вайсбергера [сформулированное С. Адлером (С. Adler) и У.
Вайсбергером (W. I. Weisberger) в 1965] для т. н. аксиальной константы бета-распада нуклона gA,
определяющей
матричный элемент аксиального тока для перехода  (экспериментальное значение gA
(экспериментальное значение gA 1,2}:
1,2}:
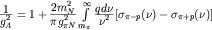 . . | (2) |
Здесь
mN -
масса нуклона,

константа связи
пи-мезона с нуклоном
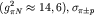
- полное сечение взаимодействия
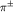
-мезонов с
протоном,
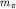
- масса пи-мезона,

и
q - его энергия и величина импульса в
лабораторной системе. Правило сумм (2) может быть представлено в виде низкоэнергетической теоремы - предсказания
для разности
длин рассеяния 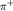
- и

-мезонов на нуклоне. Соотношение (2) хорошо (в пределах 10%) согласуется с опытом.
Остающееся расхождение связано не с нарушением
перестановочных соотношений (1), а с тем, что при выводе (2) приходится пренебрегать
массой
пи-мезона, поскольку точка нулевого 4-нмпульса пи-мезопа является нефизической.
Сочетание алгебры токов с гипотезой частичного сохранения аксиального тока (см. Аксиального тока частичное сохранение), учитывающей конечную массу
пи-мезона, оказалось особенно плодотворным для слабых и электромагнитных процессов (поскольку
многие распады частиц связаны с испусканием пи-мезонов). В общем виде амплитуда испускания пи-мезона с 4-импульсом 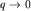 сводится к матричному элементу одновременного коммутатора гамильтониана взаимодействия
сводится к матричному элементу одновременного коммутатора гамильтониана взаимодействия 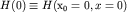 с аксиальным током:
с аксиальным током:
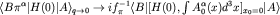 , , | (3) |
где
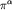
-
пионное состояние,
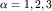
-
изотопический индекс, А, В -
адронные
состояния.
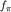
- константа
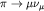
-распада [см. Вакуумный конденсат, формула (4)] (
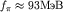
).
Гамильтониан слабого и электромагнитного взаимодействия
H(0) строится из токов
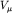
и
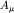
, так что алгебра токов позволяет найти одновременной
коммутатор в правой части соотношения (3). В результате возникают соотношения между амплитудами процессов с разным числом пи-мезонов, например:
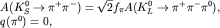 | (4) |
где
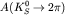
),
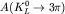
- амплитуды соответствующих слабых нелептонных распадов нейтральных короткоживущнх (
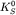
)
и
долгоживущих (
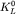
)
К-мезонов; значение амплитуды при
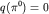
получают экстраполяцией экспериментальных данных
из физической области. Сравнение этого и других подобных соотношений с опытом позволило проверить правильность как самой алгебры токов (1), так и различных предположений
о
структуре слабого взаимодействия.
Алгебра токов и после создания современных кварковых теорий остается наиболее надежным способом описать взаимодействия адронов
при низких энергиях, исходя непосредственно из вида лагранжиана КХД (в тех случаях, когда применение
алгебры токов возможно).

