Научная Сеть >> Интерференция света

Наука >> Физика >> Общая физика >> Оптика | Обзорные статьи

Написать комментарий

Добавить новое сообщение

См. также

4 января - день рождения Исаака Ньютона

Когерентный и некогерентный свет: Как измерить время когерентности

Лабиринты фотонных кристаллов: сверхрешетка

Огонь, вода и ... мыльные нитки

Кольца Ньютона

Эффекты Джозефсона в сверхпроводниках: Сверхпроводниковые квантовые интерферометры

Корпускулярно-волновой интерферометр для макромолекул

Когерентный и некогерентный свет: Практическое значение когерентности света

Десять наиболее красивых физических экспериментов

Магматизм Земли: поляризационный микроскоп

Принципы голографии: Динамическая голография

Новые магматические горные породы.: шлиф

Динамическая голография и проблема обращения волнового фронта: Использование нелинейных сред для ОВФ

Принципы голографии: Введение

Фундаментальные взаимодействия: Гравитационное взаимодействие

Антенна: внешняя задача теории антенн

Интерференция света

Научно-образовательный сервер "Оптика",
ИТМО, Санкт-Петербург.

Содержание

Интерференция волн, испускаемых двумя точечными источниками

Два одинаковых синфазных (т.е. колеблющихся в фазе) монохроматических точечных источника S₁ и S₂ (см.рисунок), находятся на расстоянии d друг от друга. Если расстояние l до экрана, где наблюдаются интерференционные полосы, много больше расстояния между источниками( $l\gg d$ ), то амплитуды обеих волн в точке наблюдения практически одинаковы и для напряженности поля в точке P можно написать

$E=E_0\cos (kr_1-\omega t)+E_0\cos(kr_2-\omega t)=2E_0\cos [k(r_2-r_1)/2]\cos [k(r_2+r_1)/2-\omega t],$

где r₁ и r₂ - расстояние от источников до точки наблюдения P (см.рисунок).

К интерференции волн, испускаемых точечными источниками S₁ и S₂

Величину $\Delta =r_2-r_1$ называют разностью хода интерферирующих волн. Интенсивность результирующего колебания пропорциональна квадрату амплитуды, поэтому

$I=4I_0\cos^2 (k\Delta /2)=2I_0(1+\cos k\Delta)$

где I₀ - интенсивность колебаний от одного источника. Освещенность экрана в минимумах равна нулю, а в максимумах - учетверенному значению освещенности, создаваемой одним источником. Положение максимумов определяется условием $k\Delta=\pm 2\pi m$ , где целое число m = 0,1,2,... называется порядком интерференции. Учитывая, что $k=2\pi /\lambda$ , условие максимумов можно записать в виде $\Delta = m\lambda$ - разность хода равна целому числу длин волн.
В том случае, когда волны от источников распространяются не в вакууме, а в среде с показателем преломления n, последняя формула остается в силе, но в ней под 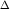$\Delta$ следует понимать не геометрическую, а оптическую разность хода интерферирующих волн: $\Delta =n(r_2-r_1)$ .
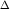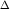Чтобы найти зависимость освещенности экрана от координаты x (см.рисунок), нужно разность хода $\Delta$ выразить через координату x точки наблюдения P. Для удобства введем угол $\theta$ , образуемый направлением на точку P с перпендикуляром к линии, соединяющей источники (т.е. с "оптической осью" рассматриваемой схемы). В практически важном случае малых значений $\theta (\theta\ll 1)$ для разности хода можно написать $\Delta\approx d\theta$ . Так как $\theta\approx x/l$ , то $\Delta\approx xd/l$ . Подставляя $\Delta$ в предыдущее выражение, получаем

$I(x)=2I_0[1+\cos (kdx/l)].$

При x = 0 расположен максимум, соответствующий нулевой разности хода. Для него порядок интерференции m = 0. Это центр интерференционной картины. Пространственный период интерференционной картины $\Delta x$ определяется из условия $kd\Delta x/l=2\pi$ , откуда $\Delta x=2\pi l/(kd)=\lambda l/d$ . Если ввести угол схождения лучей $\alpha\approx d/l$ , т.е. угол под которым видны источники из точки наблюдения, то выражение для $\Delta x$ можно записать следующим образом: $\Delta x\approx\lambda /\alpha$ . Это совпадает с уже разобранным случаем интерференции плоских волн, распространяющихся под углом $\alpha$ . В самом деле, на большом расстоянии от источников сферические волны на небольших участках приближенно можно рассматривать как плоские, угол между направлениями которых при $\theta\ll 1$ приближенно равен d/l.
Замечание.Отметим, что среднее значение освещенности по экрану в интерференционной картине, согласно формуле (5.9), равно удвоенной освещенности от одного источника. Это значит, что при интерференции происходит только перераспределение энергии в пространстве, а полный поток энергии остается неизменным. В действительности это условие приближенное и выполняется тем точнее, чем больше отношение $d/\lambda$ . В противоположном случае $d\ll\lambda$ , т.е., когда расстояние между источниками много меньше длины волны, во всех точках пространства от обоих источников происходит сложение колебаний с практически одинаковыми фазами. Это значит, что всюду интенсивность результирующих колебаний, а вместе с тем и полный поток энергии, почти в четыре раза больше, чем при одном источнике. Однако это не противоречит закону сохранения энергии, так как близко лежащие источники, взаимодействуя через создаваемое ими поле излучения, вместе излучают больше энергии, чем в том случае, когда они находятся далеко друг от друга. Для радиоволн, излучаемых близко расположенными антеннами, увеличение полного потока энергии происходит за счет работы генератора, поддерживающего неизменные амплитуды колебаний тока в антеннах. В случае свободных колебаний в источниках увеличение излучаемой энергии приводит к более быстрому их затуханию. Уменьшение времени радиационного затухания для близко расположенных одинаковых излучающих атомов известно и в оптике (сверхизлучение).
До сих пор рассматривались только точки экрана, лежащие в плоскости чертежа на рисунке. В пространстве поверхности максимальной и минимальной интенсивности представляют собой гиперболоиды вращения с фокусами в точках S₁ и S₂, так как соответствуют множеству точек, для которых разность расстояний от двух заданных точек (источников S₁ и S₂) имеет одно и тоже значение. Форма интерференционных полос на экране определяется линиями пересечения этих гиперболоидов с плоскостью экрана. В небольшой центральной области экрана полосы практически можно считать равноотстоящими параллельными прямыми, ориентированными перпендикулярно плоскости чертежа на рисунке.

Назад | Вперед

Образовательный сервер "Оптика"

Написать комментарий