Интерферометр Фабри-Перо может быть выполнен в виде плоскопараллельной стеклянной или кварцевой пластины, на обе поверхности которых нанесены отражающие слои, либо в виде двух пластин, у которых покрытые отражающими слоями плоскости установлены строго параллельно друг другу и разделены воздушным промежутком.
Отражение света от двух параллельных плоскостей приводит к образованию локализованных в бесконечности (или фокальной плоскости линзы) интерференционных полос равного наклона. В некоторую точку P фокальной плоскости линзы собираются лучи, которые до линзы образуют с ее оптической осью один и тот же угол  (см.рисунок).
 | | Полосы равного наклона при многолучевой интерференции |
Разность хода 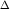 двух соседних интерферирующих лучей определяется формулой:  . Максимумы интенсивности в проходящем свете расположатся там, где 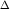составляет целое число длин волн:
Линиям равных интенсивностей соответствует одно и то же значение угла , поэтому интерференционные полосы в фокальной плоскости линзы имеют вид концентрических колец с центром на оси линзы. Центру картины соответствует наибольший порядок интерференции. При этом расположение максимумов интенсивности будет таким же, как в полосах равного наклона при двухлучевой интерференции. Однако для определения структуры максимумов в случае высокого коэффициента отражения светоделительных поверхностей необходимо учесть интерференцию всех приходящих в точку P волн, образующихся при многократных отражениях.
При каждом пересечении отражающей поверхности падающая световая волна порождает две волны: прошедшую и отраженную. Отношения амплитуд этих волн к амплитуде падающей волны (коэффициенты пропускания  и отражения  ), вообще говоря, зависят от угла падения и состояния поляризации света. Для границы двух прозрачных сред (без нанесенных на нее отражающих покрытий) это было показано с помощью формул Френеля. Мы здесь ограничимся исследованием распределения интесивности в интерференционных полосах равного наклона, которым соответствуют малые углы . В этом случае и практически не зависят от угла падения и от поляризации падающего света и для них можно принять значения, соответствующие нормальному падению.
Пусть и - амплитудные коэффициенты пропускания и отражения при переходе волны из окружающей среды в плоскопараллельную пластинку (которая, в частности, может быть воздушным промежутком между зеркалами), а  и  - при переходе из пластинки в среду. Согласно формулам Френеля,
где n и n' - показатели преломления пластинки и окружающей среды. На границе прозрачных сред и вещественны, а отрицательное значение при n>n' учитывает изменение фазы волны на  при отражении от оптически более плотной среды. Из последней формулы легко видеть, что отражательная способность границы, или энергетический коэффициент отражения R, не зависит от того, идет свет от окружающей среды в пластинку или наоборот:
и что
В случае светоделительных поверхностей с нанесенными на них многослойными непоглощающими диэлектрическими покрытиями коэффициенты  и  будут иными (в частности, отражательная способность  для определенной длины волны может иметь значения, очень близкие к единице). Но можно показать, что соотношение  остается в силе и связь  с отражательной способностью R по-прежнему выражается двумя последними формулами.
Назад | Вперед
Написать комментарий
|
