Уравнения Эйлера для идеальной жидкости.
При заданных внешних силах и известных свойствах жидкости можно записать, пользуясь 2-м законом Ньютона, уравнение движения единицы объема несжимаемой невязкой жидкости:
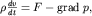
| (3.28) |
где оператор grad (градиент) определяется как
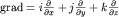
| (3.29) |
Уравнение (3.28)записано в векторном виде и является обобщением одномерного уравнения (3.3).
Расписывая (3.28) для трех проекций скорости, получаем систему уравнений
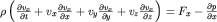
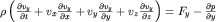
| (3.30) |
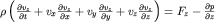
Если эти уравнения дополнить условием неразрывности
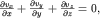
то мы получаем полную систему уравнений с четырьмя неизвестными функциями координат и времени (vx, vy, vz и p). Уравнения (3.29) называются уравнениями Эйлера и позволяют, в принципе, рассчитать динамику жидкости. Однако с математической точки зрения эта система, в отличие от многих других уравнений в физике, является нелинейной из-за наличия членов типа  . Поэтому интегрирование этих уравнений и нахождение искомых функций представляет подчас весьма сложную задачу даже при использовании мощных ЭВМ. Несложно, например, из (3.30) получить уравнение Бернулли для стационарного течения, когда . Поэтому интегрирование этих уравнений и нахождение искомых функций представляет подчас весьма сложную задачу даже при использовании мощных ЭВМ. Несложно, например, из (3.30) получить уравнение Бернулли для стационарного течения, когда 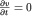 . Однако строгий вывод этого уравнения мы предоставляем читателю проделать самостоятельно, обратившись к рекомендованной литературе. Мы же будем использовать уравнения (3.30) для описания волнового движения жидкости и анализа свойств акустических волн. . Однако строгий вывод этого уравнения мы предоставляем читателю проделать самостоятельно, обратившись к рекомендованной литературе. Мы же будем использовать уравнения (3.30) для описания волнового движения жидкости и анализа свойств акустических волн.
В заключение отметим, что часто система (3.30) пишется в более компактном виде с использованием оператора градиента. Каждое из трех уравнений (3.30) имеет вид
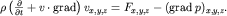
Возвращаясь к векторному представлению, получаем возможность записать 4 уравнения Эйлера (3.29) в виде двух векторных:
![$\begin{array}{l} \rho\left[\frac{\partial}{\partial t} + v \cdot {\rm grad }\right] v = F - {\rm grad }\; {p}\\ {\rm div }\; {\bf v} = 0. \end{array}$](http://images.nature.web.ru/nature/2001/06/16/0001164708/tex/formula311.gif)
| (3.31) |
Уравнение неразрывности для сжимаемой жидкости
При течении газов, особенно при больших скоростях, их плотность может заметно, а то и значительно, меняться во времени и в пространстве. Ясно, что объем втекающей жидкости может не быть равным объему вытекающей жидкости через поверхность кубика, изображенного на рис. 3.11. Если такого равенства нет, то масса газа внутри кубика (а с ней и плотность) будут со временем меняться. Уравнение (3.24) в этом случае становится несправедливым. Однако и здесь можно записать уравнение неразрывности, основная идея вывода которого базируется на балансе массы газа, составляющего физическую суть равенства (3.1). Поток массы газа через площадку dS будет равен 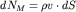 . Тогда полный поток массы газа через боковую поверхность элемента объема dxdydz, аналогично (3.27), равен . Тогда полный поток массы газа через боковую поверхность элемента объема dxdydz, аналогично (3.27), равен
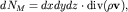
| (3.32) |
где - 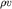 новое векторное поле. Если этот поток положительный, то масса внутри элемента новое векторное поле. Если этот поток положительный, то масса внутри элемента 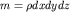 будет убывать за счет уменьшения во времени плотности . Поэтому, записывая условие баланса массы в виде будет убывать за счет уменьшения во времени плотности . Поэтому, записывая условие баланса массы в виде
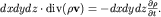
| (3.33) |
мы получаем (после сокращения на dxdydz) одно из фундаментальных уравнений гидродинамики - уравнение неразрывности сжимаемой жидкости:
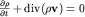
| (3.34) |
Следует отметить, что при  =const это уравнение переходит в (3.24). =const это уравнение переходит в (3.24).
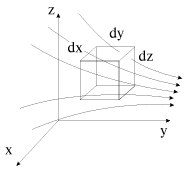 |
| Рис. 3.11. |
В электродинамике это уравнение является также фундаментальным. В самом деле, если речь идет о движущихся зарядах, объемная плотность которых равна  , то уравнение (3.34) является математическим выражением универсального закона сохранения заряда. , то уравнение (3.34) является математическим выражением универсального закона сохранения заряда.
Уравнения Эйлера и уравнение Бернулли для сжимаемой жидкости.
Динамика сжимаемой жидкости базируется также на 2-м законе Ньютона, записанном для единицы массы жидкости. Равнодействующая сил давления и внешних сил создает ускорение единицы массы, поэтому
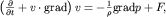
| (3.35) |
где F - внешняя сила, действующая на единицу массы. Для определения 5-ти неизвестных величин (vx, vy, vz, p и  ) необходимо дополнить (3.35) материальным уравнением, связывающим плотность и давление: ) необходимо дополнить (3.35) материальным уравнением, связывающим плотность и давление:
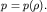
| (3.36) |
Система (3.34) - (3.36) носит название уравнений Эйлера для сжимаемой жидкости. Огромное количество задач газодинамики решается на основе анализа этих уравнений.
Воспользуемся уравнением (3.35) и получим уравнение Бернулли. Для этого видоизменим правую часть (3.35), введя вспомогательную функцию 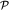 (2.27), и учтем (2.29). Тогда (3.35) примет вид (2.27), и учтем (2.29). Тогда (3.35) примет вид
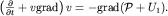
| (3.37) |
При стационарном течении 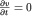 . В направлении оси трубки тока (вдоль криволинейной координаты . В направлении оси трубки тока (вдоль криволинейной координаты  ) можно записать ) можно записать
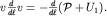
| (3.38) |
Поскольку потенциальная энергия единицы массы 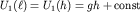 , а , а 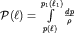 , то, по аналогии с (3.13), перепишем (3.38) в виде: , то, по аналогии с (3.13), перепишем (3.38) в виде:
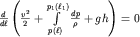
| (3.39) |
Интегрируя (3.39) вдоль трубки тока, получаем уравнение Бернулли для сжимаемой жидкости
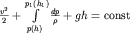
| (3.40) |
Здесь h - положение по вертикали сечения трубки тока с координатой  . Очевидно, что . Очевидно, что 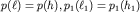 . Постоянная в (3.40) определяется заданием скорости v1 и высоты h1 в фиксированном сечении с координатой . Постоянная в (3.40) определяется заданием скорости v1 и высоты h1 в фиксированном сечении с координатой 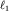 . С учетом этого, уравнение (3.40) обретает вид . С учетом этого, уравнение (3.40) обретает вид
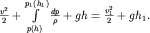
| (3.41) |
Для практического использования уравнения Бернулли необходимо знание материальной связи между p и  . Для случая несжимаемой жидкости ( . Для случая несжимаемой жидкости ( = const) уравнение (3.41) переходит в (3.15). = const) уравнение (3.41) переходит в (3.15).
Если речь идет о потоке газа, то при его быстром сжатии (увеличение плотности) газ будет нагреваться. Из-за плохой теплопроводности газа тепло не будет успевать уходить из нагретых областей. Поэтому для установления материальной связи 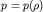 воспользуемся адиабатическим приближением: воспользуемся адиабатическим приближением:
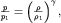
| (3.42) |
где показатель адиабаты 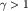 . Такая связь получается из первого начала термодинамики и уравнения состояния идеального газа (2.32) при условии отсутствия теплообмена между нагретой областью и окружающей средой. Давление в (3.42) возрастает с плотностью быстрее, чем при изотермическом процессе, так как . Такая связь получается из первого начала термодинамики и уравнения состояния идеального газа (2.32) при условии отсутствия теплообмена между нагретой областью и окружающей средой. Давление в (3.42) возрастает с плотностью быстрее, чем при изотермическом процессе, так как 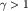 . В курсе молекулярной физики будет показано. что . В курсе молекулярной физики будет показано. что 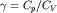 (Cp и CV - теплоемкости при постоянных давлении и объеме соответственно). Для воздуха, состоящего главным образом из двухатомных газов, (Cp и CV - теплоемкости при постоянных давлении и объеме соответственно). Для воздуха, состоящего главным образом из двухатомных газов,  = 1,4. = 1,4.
Если подставить (3.42) в (3.41) и выполнить простейшее интегрирование, то можно записать выражение для распределения давления вдоль трубки тока:
![$p = p_1\left\{ 1 - \frac{\gamma - 1}{\gamma}\frac{\rho_1}{p_1}\left[\frac{1}{2}\left( v^2 - v_1^2\right) + g(h - h_1)\right]\right\}^{\frac{\gamma}{\gamma - 1}}.$](http://images.nature.web.ru/nature/2001/06/16/0001164708/tex/formula332.gif)
| (3.43) |
Не умаляя общности, будем считать трубку тока горизонтальной (h=h1). Положим далее скорости течения такими, что
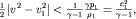
| (3.44) |
где 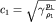 - параметр, имеющий размерность скорости. Как мы увидим несколько позднее, скорость звука в газе - параметр, имеющий размерность скорости. Как мы увидим несколько позднее, скорость звука в газе
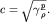
| (3.45) |
При нормальных условиях для атмосферы с=336 м/с. В этом случае (3.43) можно разложить в ряд:
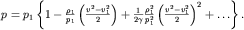
| (3.46) |
Если пренебречь квадратичным членом в (3.46), то распределение давлений соответствует течению несжимаемой жидкости с плотностью 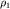 =const. Квадратичный член начинает давать вклад в распределение давлений при скоростях потока, соизмеримых со скоростью звука с1. =const. Квадратичный член начинает давать вклад в распределение давлений при скоростях потока, соизмеримых со скоростью звука с1.
Подставив (3.42) в (3.43), получаем распределение плотности вдоль трубки тока:
![$\rho = \rho_1\left\{ 1 - \frac{\gamma - 1}{\gamma}\frac{\rho_1}{p_1}\left[\frac{1}{2}\left( v^2 - v_1^2\right) + g(h - h_1)\right]\right\}^{\frac{1}{\gamma - 2}}$](http://images.nature.web.ru/nature/2001/06/16/0001164708/tex/formula337.gif)
| (3.47) |
Для горизонтальной трубки тока и при условии (3.44) распределение плотности (3.47) имеет вид:
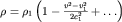
| (3.48) |
Таким образом, изменение плотности газа необходимо принимать в учет только при скоростях течения, сопоставимых по порядку величины со скоростью звука, определяемой, как следует из (3.45), давлением и плотностью в этом потоке.
Если же скорость течения 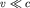 , то сжимаемостью газа можно пренебречь и оперировать с ним, как и с жидкостью. , то сжимаемостью газа можно пренебречь и оперировать с ним, как и с жидкостью.
Назад | Вперед
Посмотреть комментарии[3]
|

