




Next: 19 приведение к нормальной
Previous: 3 Канонический вид произвольных
В главе II мы познакомились с различными классами линейных
преобразований  -мерного пространства, имеющих -мерного пространства, имеющих  линейно
независимых собственных векторов. Мы знаем, что в базисе, состоящем из
собственных векторов такого преобразования, его матрица имеет особенно
простой вид, так называемую диагональную форму. линейно
независимых собственных векторов. Мы знаем, что в базисе, состоящем из
собственных векторов такого преобразования, его матрица имеет особенно
простой вид, так называемую диагональную форму.
Однако число линейно независимых собственных векторов у линейного
преобразования может быть меньше, чем  4.1.
Пример линейного преобразования с недостаточным числом собственных
векторов мы приведем несколько позже (см. также
§10, п.1, пример 3). Такое преобразование заведомо не может
быть приведено к диагональной форме, так как базис, в котором
матрица преобразования диагональна, состоит из собственных
векторов. Возникает вопрос: каков простейший вид матрицы такого
линейного преобразования? 4.1.
Пример линейного преобразования с недостаточным числом собственных
векторов мы приведем несколько позже (см. также
§10, п.1, пример 3). Такое преобразование заведомо не может
быть приведено к диагональной форме, так как базис, в котором
матрица преобразования диагональна, состоит из собственных
векторов. Возникает вопрос: каков простейший вид матрицы такого
линейного преобразования?
В этой главе мы для произвольного преобразования укажем базис, в
котором его матрица имеет сравнительно простой вид (так
называемая
жорданова нормальная форма).
В случае, когда число линейно независимых собственных векторов
преобразования равно размерности пространства, эта нормальная форма
совпадает с диагональной. Мы сформулируем сейчас окончательный
результат, который докажем в §19.
Пусть задано произвольное линейное преобразование 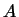 в
комплексном пространстве в
комплексном пространстве  измерений. Предположим, что у измерений. Предположим, что у 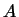 имеется
имеется 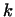
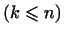 линейно независимых собственных
векторов линейно независимых собственных
векторов
 соответствующих собственным значениям
соответствующих собственным значениям
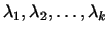 . Тогда существует
базис, состоящий из . Тогда существует
базис, состоящий из 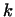 групп векторов 4.2: групп векторов 4.2:
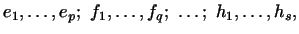 |
(1) |
в котором преобразование 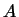 имеет следующий вид: имеет следующий вид:
Мы видим, что базисные векторы каждой группы переходят при нашем
преобразовании в линейную комбинацию векторов той же группы. Отсюда
следует, что каждая группа базисных векторов порождает
подпространство, инвариантное относительно преобразования 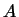 .
Рассмотрим несколько подробнее преобразование, задаваемое
формулами (2). .
Рассмотрим несколько подробнее преобразование, задаваемое
формулами (2).
В подпространстве, порожденном каждой группой, есть собственный
вектор; например, в подпространстве, порожденном векторами
 , таким собственным вектором является , таким собственным вектором является 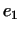 . .
Вектор 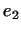 называют иногда присоединенным собственным вектором
первого порядка. Это значит, что называют иногда присоединенным собственным вектором
первого порядка. Это значит, что  пропорционально пропорционально 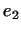 с
точностью до собственного вектора, как это видно из равенства с
точностью до собственного вектора, как это видно из равенства
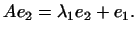 Аналогично
Аналогично
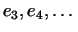 называют присоединенными
векторами второго, третьего и т.д. порядков. называют присоединенными
векторами второго, третьего и т.д. порядков.
Каждый из них является ``как бы собственным'', т.е.
собственным с точностью до присоединенного вектора низшего
порядка
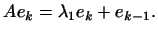
Таким образом, базис каждого инвариантного подпространства
состоит из одного собственного вектора и такого же количества
присоединенных, которое нужно добавить, чтобы получить базис
данного подпространства.
Покажем, что в каждом из этих подпространств имеется, с точностью
до множителя, лишь один собственный вектор.
Действительно, рассмотрим, например, подпространство,
порожденное векторами
 . Допустим, что
некоторый вектор из этого подпространства, т.е. некоторая
линейная комбинация вида . Допустим, что
некоторый вектор из этого подпространства, т.е. некоторая
линейная комбинация вида
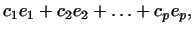 где не все
где не все  равны нулю, является собственным вектором, т.е. равны нулю, является собственным вектором, т.е.
 Подставляя вместо левой части ее выражение по формулам (2),
получаем равенство
Подставляя вместо левой части ее выражение по формулам (2),
получаем равенство
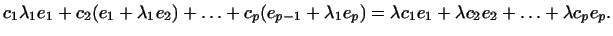 Отсюда, приравнивая коэффициенты при каждом из базисных векторов,
имеем систему уравнений для нахождения величин
Отсюда, приравнивая коэффициенты при каждом из базисных векторов,
имеем систему уравнений для нахождения величин
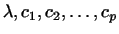 : :
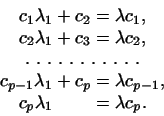 Покажем прежде всего, что
Покажем прежде всего, что
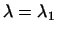 . Действительно,
если бы . Действительно,
если бы
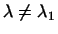 , то из последнего равенства мы
имели бы , то из последнего равенства мы
имели бы 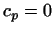 и затем из остальных равенств и затем из остальных равенств
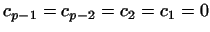 . Итак, . Итак,
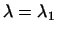 ; тогда из
первого уравнения имеем ; тогда из
первого уравнения имеем 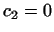 , из второго , из второго 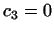 и т.д. до и т.д. до
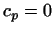 . Значит, собственный вектор равен . Значит, собственный вектор равен 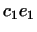 и,
следовательно, с точностью до множителя совпадает с первым
вектором соответствующей группы. и,
следовательно, с точностью до множителя совпадает с первым
вектором соответствующей группы.
Выпишем матрицу преобразования (2). Так как векторы каждой
группы преобразуются в линейные комбинации векторов той же группы, то
в первых 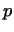 столбцах матрицы преобразования могут быть отличны от
нуля лишь элементы первых столбцах матрицы преобразования могут быть отличны от
нуля лишь элементы первых 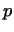 строк, в следующих строк, в следующих 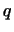 столбцах могут
быть отличны от нуля лишь элементы, стоящие в строках с теми же
номерами, что и у этих столбцов, и т.д. Таким образом, в данном
базисе матрица преобразования будет состоять из столбцах могут
быть отличны от нуля лишь элементы, стоящие в строках с теми же
номерами, что и у этих столбцов, и т.д. Таким образом, в данном
базисе матрица преобразования будет состоять из 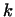 клеток,
расположенных по главной диагонали, а все элементы, не принадлежащие
ни одной из этих клеток, будут равны нулю. клеток,
расположенных по главной диагонали, а все элементы, не принадлежащие
ни одной из этих клеток, будут равны нулю.
Для того чтобы понять, что стоит в каждой клетке матрицы
преобразования 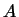 , достаточно еще раз написать, как
преобразуются векторы одной группы. Мы имеем: , достаточно еще раз написать, как
преобразуются векторы одной группы. Мы имеем:
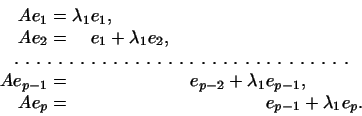 Вспоминая, как строится матрица, отвечающая данному
преобразованию базиса, получаем, что клетка матрицы,
соответствующая данной группе векторов, имеет вид
Вспоминая, как строится матрица, отвечающая данному
преобразованию базиса, получаем, что клетка матрицы,
соответствующая данной группе векторов, имеет вид
![$\displaystyle \boldsymbol{A}_1= \begin{pmatrix}\lambda_1&1&0&\dots&0&0 0&\la...
...or[1.5]{6} 0&0&0&\dots&\lambda_1&1 0&0&0&\dots&0&\lambda_1 \end{pmatrix}.$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch3img43.gif) |
(3) |
Вся же матрица оказывается составленной из таких клеток порядков
 соответственно, т.е. имеет вид соответственно, т.е. имеет вид
![\begin{equation*}\arraycolsep2.5pt \begin{pmatrix}\begin{matrix}\lambda_1&1&0&\d...
...sfor[1.5]{5} 0&0&0&\dots&\lambda_k \end{matrix} \end{pmatrix},\end{equation*}](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch3img45.gif) |
(4) |
где все элементы вне клеток -- нули.
Заметим также, что не все 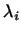 обязаны быть различными. обязаны быть различными.
Упражнение
Найти все инвариантные подпространства преобразования с
матрицей (3).
Хотя приведенная здесь нормальная форма выглядит сложнее,
чем, например, диагональная матрица, однако и с ней можно
достаточно просто производить алгебраические операции. Мы
покажем, например, как вычислить многочлен от матрицы (4).
Матрица (4) имеет вид
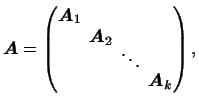 где
где
 -- отдельные клетки, а все невыписанные
элементы -- нули. Тогда -- отдельные клетки, а все невыписанные
элементы -- нули. Тогда
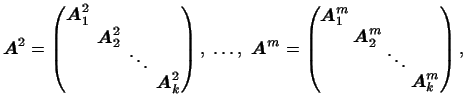 т.е. для того, чтобы возвести в некоторую степень матрицу
т.е. для того, чтобы возвести в некоторую степень матрицу
 , достаточно уметь возвести в эту степень каждую из
клеток. Пусть теперь , достаточно уметь возвести в эту степень каждую из
клеток. Пусть теперь
 --
произвольный многочлен. Тогда легко видеть, что --
произвольный многочлен. Тогда легко видеть, что
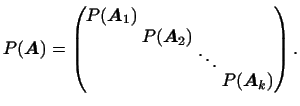
Покажем теперь, как вычислить
 , т.е. многочлен от
одной клетки нормальной формы матрицы (3). Для этого запишем
матрицу (3) в виде , т.е. многочлен от
одной клетки нормальной формы матрицы (3). Для этого запишем
матрицу (3) в виде
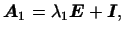 где
где
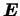 -- единичная матрица порядка -- единичная матрица порядка 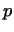 ,
а матрица ,
а матрица
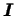 имеет вид имеет вид
![$\displaystyle \boldsymbol{I}=
\begin{pmatrix}
0&1&0&\dots&0&0\\
0&0&1&\dots&0&0\\
\hdotsfor[1.5]{6}\\
0&0&0&\dots&0&1\\
0&0&0&\dots&0&0
\end{pmatrix}.
$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch3img57.gif) Заметим, что матрицы
Заметим, что матрицы
 имеют следующий вид 4.3:
имеют следующий вид 4.3:
![$\displaystyle \boldsymbol{I}^2=
\begin{pmatrix}
0&0&1&.&\dots&0\\
0&0&0&1&\do...
...&0\\
\hdotsfor[1.5]{6}\\
0&0&0&\dots&0&0\\
0&0&0&\dots&0&0
\end{pmatrix},$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch3img70.gif) а
а
 Теперь нетрудно вычислить произвольный многочлен от матрицы (3).
Действительно, многочлен
Теперь нетрудно вычислить произвольный многочлен от матрицы (3).
Действительно, многочлен  можно по
формуле Тейлора
представить в виде можно по
формуле Тейлора
представить в виде
 где
где  -- степень многочлена. Подставляя вместо -- степень многочлена. Подставляя вместо  матрицу матрицу
 , имеем: , имеем:
 Но
Но
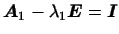 , следовательно, , следовательно,
 Подставляя вместо
Подставляя вместо
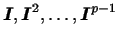 их выражения и учитывая, что их выражения и учитывая, что
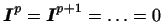 , получаем
окончательный вид матрицы , получаем
окончательный вид матрицы
 : :
![$\displaystyle P(\boldsymbol{A}_1)=
\begin{pmatrix}
P(\lambda_1)&\frac{P'(\lambd...
...a_1)}{(p-2)!}\\
\hdotsfor[1.5]{5}\\
0&0&0&\dots&P(\lambda_1)
\end{pmatrix}.$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch3img81.gif)
Мы видим, таким образом, что, для того чтобы вычислить многочлен от
одной клетки нормальной формы порядка 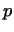 , достаточно знать значение
этого многочлена и его производных до порядка , достаточно знать значение
этого многочлена и его производных до порядка 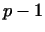 в точке в точке
 , где , где  -- собственное значение, отвечающее
клетке. Отсюда следует, что если матрица -- собственное значение, отвечающее
клетке. Отсюда следует, что если матрица
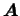 имеет
нормальную форму (4) с клетками порядков имеет
нормальную форму (4) с клетками порядков
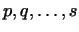 , то для
вычисления матрицы , то для
вычисления матрицы
 достаточно знать значения достаточно знать значения
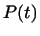 в точках в точках
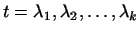 с производными
до порядков с производными
до порядков
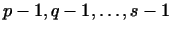 соответственно. соответственно.
Мы докажем следующую теорему.
Теорема
Пусть в комплексном  -мерном пространстве
задано линейное преобразование -мерном пространстве
задано линейное преобразование 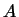 . Тогда можно найти базис, в
котором матрица линейного преобразования имеет нормальную форму.
Другими словами, можно найти базис, в котором линейное
преобразование имеет вид (2). . Тогда можно найти базис, в
котором матрица линейного преобразования имеет нормальную форму.
Другими словами, можно найти базис, в котором линейное
преобразование имеет вид (2).
Два независимых доказательства сформулированной теоремы будут даны в
§19 и 20. Кроме того, важная теория инвариантных множителей и
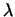 -матриц дает нам третье независимое доказательство этого
результата. -матриц дает нам третье независимое доказательство этого
результата.





Next: 19 приведение к нормальной
Previous: 3 Канонический вид произвольных
Vadim Yu. Radionov
2000-08-30
Посмотреть комментарии[2]
|


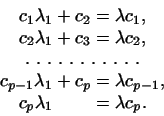 Покажем прежде всего, что
Покажем прежде всего, что
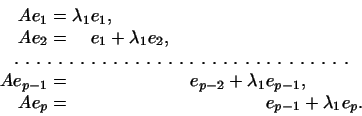 Вспоминая, как строится матрица, отвечающая данному
преобразованию базиса, получаем, что клетка матрицы,
соответствующая данной группе векторов, имеет вид
Вспоминая, как строится матрица, отвечающая данному
преобразованию базиса, получаем, что клетка матрицы,
соответствующая данной группе векторов, имеет вид
 где
где
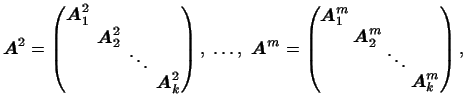 т.е. для того, чтобы возвести в некоторую степень матрицу
т.е. для того, чтобы возвести в некоторую степень матрицу
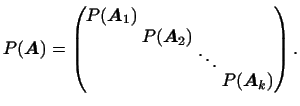
![$\displaystyle \boldsymbol{I}=
\begin{pmatrix}
0&1&0&\dots&0&0\\
0&0&1&\dots&0&0\\
\hdotsfor[1.5]{6}\\
0&0&0&\dots&0&1\\
0&0&0&\dots&0&0
\end{pmatrix}.
$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch3img57.gif) Заметим, что матрицы
Заметим, что матрицы
![$\displaystyle \boldsymbol{I}^2=
\begin{pmatrix}
0&0&1&.&\dots&0\\
0&0&0&1&\do...
...&0\\
\hdotsfor[1.5]{6}\\
0&0&0&\dots&0&0\\
0&0&0&\dots&0&0
\end{pmatrix},$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch3img70.gif) а
а
 где
где 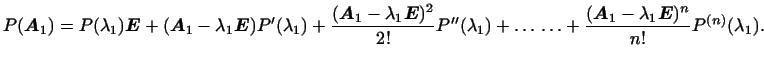 Но
Но
 Подставляя вместо
Подставляя вместо
![$\displaystyle P(\boldsymbol{A}_1)=
\begin{pmatrix}
P(\lambda_1)&\frac{P'(\lambd...
...a_1)}{(p-2)!}\\
\hdotsfor[1.5]{5}\\
0&0&0&\dots&P(\lambda_1)
\end{pmatrix}.$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch3img81.gif)