




Next: Канонический вид произвольных линейных преобразований
Previous: 16 преобразования в вещественном
Рассмотрим самосопряженное линейное преобразование  в в  -мерном
евклидовом пространстве. Мы покажем, что его собственные значения
можно получить, рассматривая некоторую задачу на минимум, связанную с
соответствующей -мерном
евклидовом пространстве. Мы покажем, что его собственные значения
можно получить, рассматривая некоторую задачу на минимум, связанную с
соответствующей  квадратичной формой квадратичной формой  . Это, в частности,
позволит доказать существование собственных векторов, не пользуясь
теоремой о существовании корня уравнения . Это, в частности,
позволит доказать существование собственных векторов, не пользуясь
теоремой о существовании корня уравнения  -й степени. Эти
экстремальные свойства полезны также при вычислении собственных
значений. Мы рассмотрим сначала вещественное пространство, а затем
перенесем полученные результаты на случай комплексного пространства. -й степени. Эти
экстремальные свойства полезны также при вычислении собственных
значений. Мы рассмотрим сначала вещественное пространство, а затем
перенесем полученные результаты на случай комплексного пространства.
Докажем сначала следующую лемму.
Лемма 17.1
Пусть 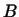 -- самосопряженное линейное преобразование в вещественном
пространстве такое, что квадратичная форма -- самосопряженное линейное преобразование в вещественном
пространстве такое, что квадратичная форма  неотрицательна,
т.е. неотрицательна,
т.е.
 для любого для любого
Тогда, если для некоторого 
 то и
то и  . .
Доказательство. Покажем, что для любого вектора  имеем имеем
 . Для этого положим . Для этого положим  , где , где  --
произвольное число, а --
произвольное число, а  -- вектор. Тогда имеем -- вектор. Тогда имеем
 т.е. так как
т.е. так как
 и и  , то , то
 для любых для любых  . Отсюда следует, что . Отсюда следует, что
 . .
Действительно, функция  при при  меняет знак в точке меняет знак в точке
 , мы же получили, что выражение , мы же получили, что выражение
 для любых
для любых  неотрицательно, следовательно, неотрицательно, следовательно,

Так как  произвольно, то произвольно, то  , что и требовалось доказать. , что и требовалось доказать.
Пусть  -- некоторое самосопряженное линейное преобразование в -- некоторое самосопряженное линейное преобразование в
 -мерном вещественном евклидовом пространстве. Соответствующую -мерном вещественном евклидовом пространстве. Соответствующую  квадратичную форму
квадратичную форму  будем рассматривать на единичной
сфере, т.е. на множестве векторов будем рассматривать на единичной
сфере, т.е. на множестве векторов 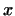 , для которых , для которых

Имеет место следующая теорема.
Теорема 17.1
Пусть  -- самосопряженное линейное преобразование. Тогда
соответствующая -- самосопряженное линейное преобразование. Тогда
соответствующая  квадратичная форма квадратичная форма  достигает на единичной
сфере минимума достигает на единичной
сфере минимума  . Вектор . Вектор 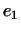 , на котором этот минимум
достигается, есть собственный вектор преобразования , на котором этот минимум
достигается, есть собственный вектор преобразования  , а значение
минимума , а значение
минимума  -- соответствующее собственное значение этого
преобразования. -- соответствующее собственное значение этого
преобразования.
Доказательство. Единичная сфера есть ограниченное замкнутое
множество в  -мерном пространстве. Поэтому -мерном пространстве. Поэтому  , как
непрерывная на нем функция, достигает минимума в некоторой точке , как
непрерывная на нем функция, достигает минимума в некоторой точке
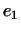 . Обозначим этот минимум через . Обозначим этот минимум через  . Тогда имеем . Тогда имеем
 если если |
(1) |
причем
 где где
Запишем неравенство (1) в виде
 где где |
(2) |
Оно справедливо для векторов длины единица. Так как при умножении 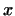 на некоторое число
на некоторое число  как правая, так и левая части неравенства
умножаются на как правая, так и левая части неравенства
умножаются на  , то оно справедливо для векторов любой длины
(поскольку любой вектор можно получить из вектора длины единица
умножением его на некоторое число , то оно справедливо для векторов любой длины
(поскольку любой вектор можно получить из вектора длины единица
умножением его на некоторое число  ). ).
Полученное неравенство можно переписать так:
 для любых для любых причем для
причем для  имеет место имеет место

Это значит, что преобразование
 удовлетворяет условиям
леммы 1. Отсюда, применяя эту лемму, получаем: удовлетворяет условиям
леммы 1. Отсюда, применяя эту лемму, получаем:
 т. е. т. е.
Таким образом, 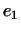 является собственным вектором преобразования является собственным вектором преобразования  ,
соответствующим собственному значению ,
соответствующим собственному значению  . Теорема доказана. . Теорема доказана.
Для нахождения следующего собственного значения рассмотрим все векторы
из  , ортогональные к собственному вектору , ортогональные к собственному вектору 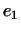 . Как было показано
в п.2 §16 (лемма 2), эти векторы образуют . Как было показано
в п.2 §16 (лемма 2), эти векторы образуют 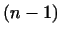 -мерное
подпространство -мерное
подпространство  , инвариантное относительно преобразования , инвариантное относительно преобразования  . .
Отыскивая минимум квадратичной формы  , при условии , при условии  ,
в этом подпространстве мы придем к новому собственному вектору ,
в этом подпространстве мы придем к новому собственному вектору 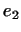 и
собственному значению и
собственному значению  . .
Очевидно, что
 , так как минимум , так как минимум  во всем пространстве не может быть больше, чем минимум той же функции
в подпространстве.
во всем пространстве не может быть больше, чем минимум той же функции
в подпространстве.
Следующий собственный вектор мы получим, решая ту же задачу в
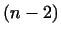 -мерном инвариантном подпространстве, состоящем из векторов,
ортогональных и -мерном инвариантном подпространстве, состоящем из векторов,
ортогональных и 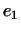 и и 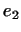 . Значение минимума . Значение минимума  в этом
подпространстве будет третьим собственным значением. в этом
подпространстве будет третьим собственным значением.
Продолжая этот процесс, мы исчерпаем все  собственных значений и
соответствующих им собственных векторов нашего преобразования. собственных значений и
соответствующих им собственных векторов нашего преобразования.
Иногда бывает полезно определить второй, третий и т.д. собственные
векторы преобразования из задачи на максимум или минимум
непосредственно, не считая при этом известными предыдущие собственные
векторы.
Пусть  -- самосопряженное линейное преобразование. Обозначим через -- самосопряженное линейное преобразование. Обозначим через
 его собственные значения, расположенные в возрастающем порядке, а
через
его собственные значения, расположенные в возрастающем порядке, а
через
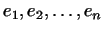 -- соответствующие им нормированные и
ортогональные собственные векторы. -- соответствующие им нормированные и
ортогональные собственные векторы.
Покажем, что если мы возьмем первые  собственных векторов собственных векторов
 и порожденное ими подпространство
и порожденное ими подпространство  , то для любого вектора , то для любого вектора
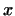 из из  имеет место неравенство имеет место неравенство
 Действительно, пусть
Действительно, пусть
 Так как
Так как
 , ,
 , ,
 при при
 , то , то

Кроме того, так как векторы
 ортогональны и нормированы, то
ортогональны и нормированы, то
 и, следовательно,
и, следовательно,
 Аналогично
Аналогично
 и, следовательно,
и, следовательно,

Пусть теперь  -- произвольное подпространство -- произвольное подпространство  измерений. В §7 (лемма п.1) мы доказали, что если сумма
размерностей двух подпространств
измерений. В §7 (лемма п.1) мы доказали, что если сумма
размерностей двух подпространств  -мерного пространства превышает -мерного пространства превышает
 , то существует отличный от нуля вектор, принадлежащий обоим
подпространствам. Следовательно, так как , то существует отличный от нуля вектор, принадлежащий обоим
подпространствам. Следовательно, так как
 , то существует
вектор , то существует
вектор 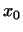 , принадлежащий как , принадлежащий как  , так и подпространству , так и подпространству  ,
порожденному векторами ,
порожденному векторами
 . Мы можем считать, что
длина его равна 1, т.е. что . Мы можем считать, что
длина его равна 1, т.е. что
 . Так как всюду в . Так как всюду в  , как мы
уже доказали, , как мы
уже доказали,
 , то , то
 . .
Итак, мы доказали, что в  существует вектор существует вектор 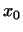 длины 1
такой, что длины 1
такой, что
 Но тогда и подавно, минимум
Но тогда и подавно, минимум  , где , где 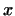 пробегает все
векторы длины 1 из пробегает все
векторы длины 1 из  , также меньше или равен , также меньше или равен  . .
Таким образом, для любого  -мерного подпространства -мерного подпространства

 где
где  и и  . .
Заметим, что среди подпространств  размерности размерности  есть
такое, для которого есть
такое, для которого
 , ,  , ,  , в точности
равен , в точности
равен  . Таким подпространством является подпространство,
состоящее из векторов, ортогональных первым . Таким подпространством является подпространство,
состоящее из векторов, ортогональных первым  собственным векторам собственным векторам
 . Действительно, в этом параграфе мы
доказали, что . Действительно, в этом параграфе мы
доказали, что
 , распространенный по всем
векторам, ортогональным первым , распространенный по всем
векторам, ортогональным первым  собственным векторам, равен собственным векторам, равен
 . .
Итак, мы доказали следующее утверждение:
Пусть  -- некоторое -- некоторое  -мерное подпространство
пространства -мерное подпространство
пространства  . Тогда минимум . Тогда минимум  для всех для всех 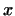 из из  таких, что
таких, что  , меньше или равен , меньше или равен  .
Подпространство .
Подпространство  можно выбрать так, чтобы этот минимум
равнялся можно выбрать так, чтобы этот минимум
равнялся  . .
Это утверждение можно записать следующей формулой:
 |
(3) |
В этой формуле  берется по указанным векторам, а берется по указанным векторам, а  по
всевозможным подпространствам по
всевозможным подпространствам  размерности размерности  . .
Из доказанной теоремы следует:
Пусть  -- самосопряженное линейное преобразование, а -- самосопряженное линейное преобразование, а 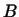 --
положительно определенное линейное преобразование. Пусть --
положительно определенное линейное преобразование. Пусть
 --
собственные значения --
собственные значения  , а , а
 --
собственные значения --
собственные значения  ; тогда ; тогда
 . .
Действительно, всюду

Следовательно, в любом  -мерном подпространстве -мерном подпространстве  имеет
место неравенство: имеет
место неравенство:

Значит, максимум левой части по всевозможным подпространствам  не
превосходит максимума правой части. Так как в силу формулы максимум
левой части равен не
превосходит максимума правой части. Так как в силу формулы максимум
левой части равен  , а максимум правой равен , а максимум правой равен  , то , то
 , что и требовалось доказать. , что и требовалось доказать.
Перенесем полученные результаты на случай комплексного пространства.
Для этого нам придется заменить лишь лемму 1 следующей леммой.
Лемма 17.2
Пусть 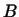 -- самосопряженное преобразование в
комплексном пространстве, и соответствующая ему эрмитова форма -- самосопряженное преобразование в
комплексном пространстве, и соответствующая ему эрмитова форма
 не отрицательна, т.е. не отрицательна, т.е.
 для любых для любых
Тогда, если для некоторого 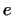  , то и , то и
 . .
Доказательство. Пусть  -- произвольное вещественное число, а -- произвольное вещественное число, а
 -- вектор. Тогда -- вектор. Тогда
 или, так как
или, так как  , то , то
![$\displaystyle t[(Be,h)+(Bh,e)]+t^2(Bh,h)\geqslant0
$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img734.gif) для любого
для любого  . Отсюда следует, что . Отсюда следует, что
 |
(4) |
Так как  произвольно, то, заменяя произвольно, то, заменяя  на на  , получаем , получаем
 , т.е. , т.е.
 |
(5) |
Из (4) и (5) получаем, что
 и так как
и так как  произвольно, то произвольно, то  . Лемма доказана. . Лемма доказана.
Все остальные теоремы этого параграфа и их доказательства переносятся
на случай комплексного пространства без всяких изменений.





Next: Канонический вид произвольных линейных преобразований
Previous: 16 преобразования в вещественном
Vadim Yu. Radionov
2000-08-30
Посмотреть комментарии[2]
|

