




Next: 11 линейное преобразование, сопряженное
Previous: 9 линейные преобразования и
Subsections
Пусть  -- подпространство пространства -- подпространство пространства  и и  -- линейное
преобразование в -- линейное
преобразование в  . Вообще говоря, для произвольного . Вообще говоря, для произвольного
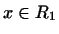 , ,
 3.1.
Например, если 3.1.
Например, если  -- евклидова плоскость, -- евклидова плоскость,  -- произвольная
прямая и -- произвольная
прямая и  -- поворот на угол -- поворот на угол
 , то
очевидно, что для любого , то
очевидно, что для любого  и принадлежащего и принадлежащего  , ,
 . Однако может случиться, что некоторые подпространства переходят
сами в себя при линейном преобразовании . Однако может случиться, что некоторые подпространства переходят
сами в себя при линейном преобразовании  . Введем следующие
определения. . Введем следующие
определения.
Определение 10.1
Пусть  -- линейное преобразование
пространства -- линейное преобразование
пространства  . Линейное подпространство . Линейное подпространство  называется
инвариантным
относительно называется
инвариантным
относительно  , если для каждого вектора , если для каждого вектора 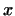 из из  вектор вектор  также принадлежит
также принадлежит  . .
При изучении линейного преобразования  в инвариантном
подпространстве в инвариантном
подпространстве  можно, таким образом, рассматривать это
преобразование только в можно, таким образом, рассматривать это
преобразование только в  . .
Тривиальными инвариантными подпространствами являются подпространство,
состоящее лишь из нуля, и все пространство.
Примеры
1. Пусть  -- трехмерное пространство и -- трехмерное пространство и  -- поворот вокруг
некоторой оси, проходящей через нуль. Инвариантными подпространствами
при этом являются: а) ось вращения (одномерное инвариантное
подпространство), б) плоскость, проходящая через начало координат и
ортогональная к этой оси (двумерное инвариантное подпространство). -- поворот вокруг
некоторой оси, проходящей через нуль. Инвариантными подпространствами
при этом являются: а) ось вращения (одномерное инвариантное
подпространство), б) плоскость, проходящая через начало координат и
ортогональная к этой оси (двумерное инвариантное подпространство).
2.  -- плоскость. Преобразование -- плоскость. Преобразование  заключается в растяжении
плоскости в заключается в растяжении
плоскости в  раз вдоль оси раз вдоль оси  и в и в  раз
вдоль оси раз
вдоль оси  . Иначе говоря, если вектор . Иначе говоря, если вектор 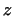 равен равен
 , то , то
 ,
где ,
где  -- единичные векторы на осях. Координатные
оси -- единичные векторы на осях. Координатные
оси  и и  являются в этом случае одномерными инвариантными
подпространствами. Если являются в этом случае одномерными инвариантными
подпространствами. Если
 , то , то  является
преобразованием подобия с коэффициентом подобия является
преобразованием подобия с коэффициентом подобия 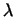 .
В этом случае каждая прямая, проходящая через начало
координат, является инвариантным подпространством. .
В этом случае каждая прямая, проходящая через начало
координат, является инвариантным подпространством.
Упражнение
Показать, что если
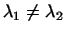 , то в примере 2 нет никаких
других одномерных инвариантных подпространств, кроме указанных выше. , то в примере 2 нет никаких
других одномерных инвариантных подпространств, кроме указанных выше.
3.  -- совокупность многочленов степени не выше -- совокупность многочленов степени не выше  . Линейное
преобразование . Линейное
преобразование  -- дифференцирование, т.е. -- дифференцирование, т.е.
 Совокупность многочленов, степень которых меньше или равна
Совокупность многочленов, степень которых меньше или равна  , где , где
 , образует инвариантное подпространство.
Действительно, дифференцируя многочлен степени , образует инвариантное подпространство.
Действительно, дифференцируя многочлен степени
 , мы
получим многочлен, степень которого снова не превосходит , мы
получим многочлен, степень которого снова не превосходит  . .
Упражнение
Доказать, что в примере 3 никаких инвариантных подпространств, кроме
указанных, нет.
4.  -- произвольное -- произвольное  -мерное пространство. Линейное
преобразование -мерное пространство. Линейное
преобразование  задается в некотором базисе задается в некотором базисе
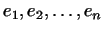 матрицей вида
матрицей вида
![$\displaystyle \arraycolsep3pt
\begin{pmatrix}
a_{11}&\dots&a_{1k}&a_{1,k+1}&\do...
...1,n}\\
\hdotsfor[1.5]{6}\\
0&\dots&0&a_{n,k+1}&\dots&a_{nn}
\end{pmatrix}.
$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img241.gif) В этом случае подпространство
В этом случае подпространство  , порожденное векторами , порожденное векторами
 , инвариантно. Доказательство этого мы
предоставляем читателю. Если, кроме того, , инвариантно. Доказательство этого мы
предоставляем читателю. Если, кроме того,
 то подпространство, порожденное векторами
то подпространство, порожденное векторами
 , также будет инвариантным. , также будет инвариантным.
5.  -- произвольное -- произвольное  -мерное пространство, -мерное пространство,  --
произвольное линейное преобразование в этом пространстве. --
произвольное линейное преобразование в этом пространстве.
Тогда образ  и ядро и ядро  преобразования преобразования  являются
инвариантными подпространствами. Действительно, пусть являются
инвариантными подпространствами. Действительно, пусть  .
Тогда .
Тогда  в силу определения в силу определения  . .
Точно так же, если  , то , то  . .
Этот простой факт будет использован в дальнейшем при приведении
произвольного преобразования к простейшему виду.
Пусть дано пространство  и линейное преобразование и линейное преобразование  в этом
пространстве. Предположим, что в этом
пространстве. Предположим, что  разложимо в
прямую сумму
двух инвариантных подпространств разложимо в
прямую сумму
двух инвариантных подпространств  размерности размерности  и и 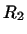 размерности
размерности  (см. стр. (см. стр.![[*]](http://images.nature.web.ru/nature/2000/10/02/0001151602/crossref.png) ). Тогда в базисе ). Тогда в базисе
 , первые , первые  векторов которого лежат в векторов которого лежат в  , а последние , а последние
 -- в -- в 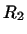 , матрица преобразования , матрица преобразования  состоит из двух клеток
размерностей состоит из двух клеток
размерностей  и и  , стоящих на диагонали, а на остальных местах
стоят нули, т.е. , стоящих на диагонали, а на остальных местах
стоят нули, т.е.
![$\displaystyle \arraycolsep3pt
\boldsymbol{A}=
\begin{pmatrix}
a_{11}&\dots&a_{1...
...{6}\\
\hdotsfor[1.5]{6}\\
0&\dots&0&a_{n,k+1}&\dots&a_{n,n}
\end{pmatrix}.
$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img250.gif)
Особую роль в дальнейшем будут играть одномерные инвариантные
подпространства.
Пусть  -- одномерное подпространство, порожденное вектором -- одномерное подпространство, порожденное вектором
 (т.е. совокупность векторов вида (т.е. совокупность векторов вида  ). Ясно, что
для того чтобы ). Ясно, что
для того чтобы  было инвариантным, необходимо и достаточно,
чтобы вектор было инвариантным, необходимо и достаточно,
чтобы вектор  лежал в лежал в  , т.е. был кратен вектору , т.е. был кратен вектору 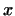 : :

Определение 10.2
Вектор  , удовлетворяющий соотношению , удовлетворяющий соотношению
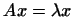 , называется
собственным вектором,
а соответствующее число , называется
собственным вектором,
а соответствующее число 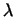 --
собственным значением (характеристическим числом)
линейного преобразования --
собственным значением (характеристическим числом)
линейного преобразования  . .
Итак, если 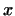 -- собственный вектор, то векторы -- собственный вектор, то векторы  образуют
одномерное инвариантное подпространство. образуют
одномерное инвариантное подпространство.
Обратно, все отличные от нуля векторы одномерного инвариантного
подпространства являются собственными.
Теорема 10.1
В
комплексном пространстве3.2
 всякое линейное преобразование всякое линейное преобразование  имеет хотя бы один собственный
вектор. имеет хотя бы один собственный
вектор.
Доказательство. Выберем в  какой-либо базис какой-либо базис
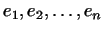 . Линейному
преобразованию . Линейному
преобразованию  в этом базисе соответствует некоторая матрица в этом базисе соответствует некоторая матрица
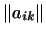 . .
Пусть
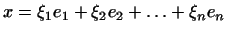 -- произвольный вектор из
-- произвольный вектор из  . Тогда координаты . Тогда координаты
 вектора вектора  выражаются
следующими формулами (см. п.2 §9): выражаются
следующими формулами (см. п.2 §9):
 Условие того, что вектор собственный, т.е. равенство
Условие того, что вектор собственный, т.е. равенство
 записывается в следующем виде:
записывается в следующем виде:
 или
или
Для доказательства теоремы нужно доказать, таким образом, что
существуют число 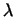 и числа и числа
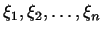 , не
все равные нулю, удовлетворяющие системе (1). , не
все равные нулю, удовлетворяющие системе (1).
Условием существования ненулевого решения однородной системы (1)
является равенство нулю ее определителя
 |
(2) |
Мы получили уравнение степени  относительно относительно 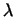 . Это
уравнение имеет хотя бы один (вообще говоря, комплексный)
корень . Это
уравнение имеет хотя бы один (вообще говоря, комплексный)
корень  . .
Подставив в систему (1) вместо 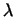 корень корень  , мы
получим однородную систему линейных уравнений, определитель которой
равен нулю, и имеющую, следовательно, ненулевое решение , мы
получим однородную систему линейных уравнений, определитель которой
равен нулю, и имеющую, следовательно, ненулевое решение
 . Тогда вектор . Тогда вектор
 будет собственным вектором, а
будет собственным вектором, а  -- собственным
значением, так как -- собственным
значением, так как
 Теорема доказана.
Теорема доказана.
Замечание
Так как доказательство теоремы остается в силе, если
преобразование  рассматривать не во всем пространстве, а в любом
его инвариантном подпространстве, то в любом инвариантном
подпространстве существует хотя бы один собственный вектор
преобразования рассматривать не во всем пространстве, а в любом
его инвариантном подпространстве, то в любом инвариантном
подпространстве существует хотя бы один собственный вектор
преобразования  . .
Многочлен, стоящий в левой части уравнения (2), называется
характеристическим многочленом
матрицы преобразования  , а само уравнение (2)
характеристическим или вековым уравнением
этой матрицы. В процессе доказательства теоремы мы показали, что корни
характеристического многочлена суть собственные значения
преобразования , а само уравнение (2)
характеристическим или вековым уравнением
этой матрицы. В процессе доказательства теоремы мы показали, что корни
характеристического многочлена суть собственные значения
преобразования  и, обратно, собственные значения преобразования и, обратно, собственные значения преобразования  суть корни характеристического многочлена.
суть корни характеристического многочлена.
Так как собственные значения преобразования определены независимо от
выбора базиса, то, следовательно, и корни характеристического
многочлена также не зависят от выбора базиса. Мы покажем далее
несколько больше 3.3,
а именно, что сам характеристический многочлен не зависит от
выбора базиса, и поэтому мы в дальнейшем будем называть его
характеристическим многочленом преобразования  (а не
характеристическим многочленом матрицы преобразования (а не
характеристическим многочленом матрицы преобразования  ). ).
Среди линейных преобразований в известном смысле простейшими являются
те, которые имеют  линейно независимых собственных векторов. линейно независимых собственных векторов.
Пусть  -- такое преобразование, а -- такое преобразование, а
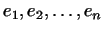 -- его
линейно независимые собственные векторы, т.е. -- его
линейно независимые собственные векторы, т.е.
 Примем
Примем
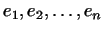 за базис в за базис в  . Равенства . Равенства
 означают, что матрица преобразования
означают, что матрица преобразования  в этом базисе имеет вид в этом базисе имеет вид
 (является диагональной матрицей). Таким образом, имеет
место
(является диагональной матрицей). Таким образом, имеет
место
Теорема 10.2
Если линейное преобразование  имеет имеет  линейно независимых
собственных векторов, то, выбрав их за базис, мы приведем матрицу
преобразования линейно независимых
собственных векторов, то, выбрав их за базис, мы приведем матрицу
преобразования  к диагональной форме. Обратно, если в некотором
базисе матрица преобразования диагональна, то все векторы этого базиса
являются собственными векторами. к диагональной форме. Обратно, если в некотором
базисе матрица преобразования диагональна, то все векторы этого базиса
являются собственными векторами.
Замечание
Отметим один важный случай, когда линейное преобразование заведомо
имеет  линейно независимых собственных векторов. Предварительно
заметим следующее: линейно независимых собственных векторов. Предварительно
заметим следующее:
Если
 -- собственные векторы
преобразования -- собственные векторы
преобразования  и соответствующие им собственные значения и соответствующие им собственные значения
 , попарно различны,
то , попарно различны,
то
 линейно независимы. линейно независимы.
Для  утверждение очевидно. Пусть наше утверждение верно для утверждение очевидно. Пусть наше утверждение верно для  векторов; докажем его для
векторов; докажем его для  векторов. Предположим противное, т.е.
предположим, что векторов. Предположим противное, т.е.
предположим, что
 |
(3) |
причем хотя бы один из коэффициентов  , например , например
 , отличен от нуля. , отличен от нуля.
Применим к обеим частям равенства (3) преобразование  .
Получим .
Получим
 т.е.
т.е.
 Вычитая из последнего равенства равенство (3), умноженное
на
Вычитая из последнего равенства равенство (3), умноженное
на  , мы получим выражение , мы получим выражение
 где первый коэффициент по-прежнему отличен от нуля (так как по условию
где первый коэффициент по-прежнему отличен от нуля (так как по условию
 при при  ). Мы пришли к противоречию, так
как по индуктивному предположению векторы ). Мы пришли к противоречию, так
как по индуктивному предположению векторы
 линейно независимы. Отсюда непосредственно следует, что:
линейно независимы. Отсюда непосредственно следует, что:
Если характеристический многочлен преобразования  имеет имеет
 различных корней, то матрица преобразования различных корней, то матрица преобразования  может быть
приведена к диагональной форме. может быть
приведена к диагональной форме.
Действительно, каждому корню  характеристического уравнения
отвечает хотя бы один собственный вектор. Так как соответствующие этим
векторам собственные значения (корни характеристического уравнения)
все различны, то, согласно доказанному выше, мы имеем характеристического уравнения
отвечает хотя бы один собственный вектор. Так как соответствующие этим
векторам собственные значения (корни характеристического уравнения)
все различны, то, согласно доказанному выше, мы имеем  линейно
независимых собственных векторов линейно
независимых собственных векторов
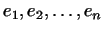 . Если векторы . Если векторы
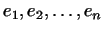 принять за базис, то матрица преобразования принять за базис, то матрица преобразования  будет диагональной.
будет диагональной.
Если характеристический многочлен имеет кратные корни, то число
линейно независимых собственных векторов может быть меньше,
чем  . Например, преобразование . Например, преобразование  в пространстве многочленов
степени не выше в пространстве многочленов
степени не выше  , ставящее в соответствие каждому многочлену его
производную, имеет лишь одно собственное значение , ставящее в соответствие каждому многочлену его
производную, имеет лишь одно собственное значение  и один
(с точностью до пропорциональности) собственный вектор и один
(с точностью до пропорциональности) собственный вектор
 .
В самом деле, для любого многочлена .
В самом деле, для любого многочлена  степени степени  многочлен многочлен
 имеет степень имеет степень  , и потому равенство , и потому равенство
 возможно лишь, если
возможно лишь, если  и и
 . Следовательно, для
этого преобразования не существует базиса, в котором ему
соответствовала бы диагональная матрица. . Следовательно, для
этого преобразования не существует базиса, в котором ему
соответствовала бы диагональная матрица.
В главе III будет доказано, что если 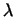 есть есть  -кратный корень
характеристического уравнения, то ему отвечает не более чем -кратный корень
характеристического уравнения, то ему отвечает не более чем  линейно независимых собственных векторов.
линейно независимых собственных векторов.
Ниже (в §§12 и 13) мы укажем некоторые классы линейных
преобразований, приводимых к диагональной форме. Вопросу о том, к
какому простейшему виду может быть приведено произвольное линейное
преобразование, будет посвящена глава III.
В п.2 мы уже определили
характеристический многочлен преобразования  как
определитель матрицы как
определитель матрицы
 ,
где ,
где
 -- матрица преобразования -- матрица преобразования  ,
а ,
а
 -- единичная матрица.
Докажем, что характеристический многочлен не зависит от выбора
базиса. Действительно, при переходе к другому базису матрица -- единичная матрица.
Докажем, что характеристический многочлен не зависит от выбора
базиса. Действительно, при переходе к другому базису матрица
 преобразования преобразования  принимает вид принимает вид
 , где , где
 есть матрица
перехода к новому базису. Таким образом, в новом базисе характеристический
многочлен есть определитель матрицы есть матрица
перехода к новому базису. Таким образом, в новом базисе характеристический
многочлен есть определитель матрицы
 . Но . Но
 и так как определитель произведения равен произведению
определителей, то
и так как определитель произведения равен произведению
определителей, то
 и утверждение доказано. Таким образом, мы в дальнейшем можем говорить
о характеристическом многочлене преобразования
и утверждение доказано. Таким образом, мы в дальнейшем можем говорить
о характеристическом многочлене преобразования  (а не о
характеристическом многочлене матрицы преобразования (а не о
характеристическом многочлене матрицы преобразования  ). ).
Упражнения
1. Найти характеристический многочлен матрицы
![$\displaystyle \arraycolsep3pt
\begin{pmatrix}
\lambda_0&0&0&\dots&0&0\\
1&\la...
...a_0&\dots&0&0\\
\hdotsfor[1.5]{6}\\
0&0&0&\dots&1&\lambda_0
\end{pmatrix}.
$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img290.gif)
2. Найти характеристический многочлен матрицы
![$\displaystyle \arraycolsep3pt
\begin{pmatrix}
a_1&a_2&a_3&\dots&a_{n-1}&a_n ...
...0\\
0&1&0&\dots&0&0\\
\hdotsfor[1.5]{6}\\
0&0&0&\dots&1&0
\end{pmatrix}.
$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img291.gif) Ответ.
Ответ.
 . .
Выразим характеристический многочлен явно через элементы матрицы
 преобразования преобразования  . Вычислим сначала более общий
определитель (который позже в §12 нам тоже встретится): . Вычислим сначала более общий
определитель (который позже в §12 нам тоже встретится):
 , где , где
 и и
 -- две заданные матрицы. Нам нужно, следовательно,
вычислить следующий многочлен относительно -- две заданные матрицы. Нам нужно, следовательно,
вычислить следующий многочлен относительно 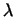 : :
 Так как в этом определителе каждый столбец есть сумма двух
столбцов, то определитель может быть разложен на сумму
определителей. Свободный член в
Так как в этом определителе каждый столбец есть сумма двух
столбцов, то определитель может быть разложен на сумму
определителей. Свободный член в
 есть есть
![$\displaystyle q_0=\begin{vmatrix}a_{11}&a_{12}&\dots&a_{1n} a_{21}&a_{22}&\dots&a_{2n} \hdotsfor[1.5]{4} a_{n1}&a_{n2}&\dots&a_{nn} \end{vmatrix}.$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img296.gif) |
(4) |
Ясно, что коэффициент при
 в в
 равен
сумме определителей, каждый из которых получается заменой в
(4) каких-либо равен
сумме определителей, каждый из которых получается заменой в
(4) каких-либо  столбцов матрицы столбцов матрицы
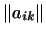 соответствующими столбцами матрицы
соответствующими столбцами матрицы
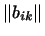 . .
Перейдем теперь к вычислению
 .
Для вычисления коэффициента при .
Для вычисления коэффициента при
 мы должны взять сумму
определителей, каждый из которых получается заменой мы должны взять сумму
определителей, каждый из которых получается заменой  столбцов
матрицы столбцов
матрицы
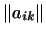  столбцами единичной матрицы. Но каждый такой
определитель есть главный минор столбцами единичной матрицы. Но каждый такой
определитель есть главный минор  -го порядка
матрицы -го порядка
матрицы
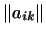 . Таким образом, окончательно,
характеристический многочлен . Таким образом, окончательно,
характеристический многочлен
 матрицы матрицы
 имеет вид имеет вид
 где
где  есть сумма диагональных элементов, есть сумма диагональных элементов,  -- сумма
главных миноров
второго порядка и т.д.; наконец -- сумма
главных миноров
второго порядка и т.д.; наконец  есть определитель
матрицы есть определитель
матрицы
 . .
Числа
 , построенные по матрице , построенные по матрице
 преобразования
преобразования  , зависят лишь от самого
преобразования, поскольку этим свойством, как мы показали,
обладает характеристический многочлен. Среди коэффициентов , зависят лишь от самого
преобразования, поскольку этим свойством, как мы показали,
обладает характеристический многочлен. Среди коэффициентов  наибольшую роль играют
наибольшую роль играют  -- определитель матрицы -- определитель матрицы
 и и
 -- сумма диагональных элементов матрицы -- сумма диагональных элементов матрицы
 .
Сумма диагональных элементов матрицы называется
следом матрицы .
Сумма диагональных элементов матрицы называется
следом матрицы
 . След матрицы . След матрицы
 обозначается обозначается
 (от английского слова trace -- след). Ясно, что
след матрицы равен сумме всех корней характеристического многочлена
(собственных значений), причем каждый корень считается с той
кратностью, с которой он входит в характеристический многочлен. (от английского слова trace -- след). Ясно, что
след матрицы равен сумме всех корней характеристического многочлена
(собственных значений), причем каждый корень считается с той
кратностью, с которой он входит в характеристический многочлен.
Упражнения
1. Показать, что если
 и и
 --
матрицы --
матрицы  -го порядка, то -го порядка, то

2. Показать, что если
 -- невырожденная матрицы -- невырожденная матрицы  -го
порядка, то для любой матрицы -го
порядка, то для любой матрицы
  -го порядка имеем: -го порядка имеем:

Вычисление собственных векторов линейного преобразования требует
знания собственных значений и, следовательно, решения уравнения  -й
степени -- характеристического уравнения. В одном важном частном
случае корни характеристического многочлена можно найти
непосредственно. -й
степени -- характеристического уравнения. В одном важном частном
случае корни характеристического многочлена можно найти
непосредственно.
Если матрица преобразования  треугольная, т.е. имеет вид треугольная, т.е. имеет вид
![\begin{equation*}\begin{pmatrix}a_{11}&a_{12}&a_{13}&\dots&a_{1n} 0&a_{22}&a_...
...vskip-2pt} \hdotsfor[1.5]{5} 0&0&0&\dots&a_{nn} \end{pmatrix},\end{equation*}](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img309.gif) |
(5) |
то собственными значениями будут числа, стоящие на диагонали,
т.е.
 . .
В самом деле, характеристический многочлен данной матрицы вычисляется
непосредственно и есть
 и следовательно, его корни --
и следовательно, его корни --
 . .
Упражнение
Найти собственные векторы, отвечающие собственным
значениям
 треугольной матрицы (5). треугольной матрицы (5).
В заключение этого пункта укажем одно интересное свойство
характеристического многочлена. Как мы уже указывали в п.3
предыдущего параграфа, существует такой многочлен  , что если в
него подставить вместо , что если в
него подставить вместо  матрицу матрицу
 , то он обратится в
нуль. Мы покажем сейчас, что одним из таких многочленов является
характеристический многочлен. Докажем предварительно лемму: , то он обратится в
нуль. Мы покажем сейчас, что одним из таких многочленов является
характеристический многочлен. Докажем предварительно лемму:
Лемма
Пусть многочлен
 и матрица
и матрица
 связаны соотношением связаны соотношением
 |
(6) |
где
 -- многочлен от -- многочлен от 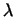 ,
коэффициенты которого являются матрицами, т.е. ,
коэффициенты которого являются матрицами, т.е.
 -- матрицы -- матрицы Тогда
Тогда
 . .
Заметим, что эта лемма является обобщением на многочлены с матричными
коэффициентами
теоремы Безу.
Доказательство. Мы имеем:
 |
(7) |
Сравнивая между собой коэффициенты при одинаковых степенях 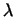 в
обеих частях равенства (6), мы получаем последовательность равенств: в
обеих частях равенства (6), мы получаем последовательность равенств:
Умножим теперь слева первое равенство на
 , второе
на , второе
на
 , третье на , третье на
 , ,  , последнее
на , последнее
на
 и сложим их. Мы получим справа и сложим их. Мы получим справа
 , а слева 0. Таким образом, , а слева 0. Таким образом,
 и лемма доказана 3.4.
и лемма доказана 3.4.
Теорема 10.3
Если
 -- характеристический многочлен матрицы -- характеристический многочлен матрицы
 , то , то
 . .
Доказательство. Рассмотрим матрицу, обратную матрице
 . Мы имеем . Мы имеем
 . Как известно, обратная
матрица может быть записана в виде . Как известно, обратная
матрица может быть записана в виде
 где
где
 -- матрица из миноров -- матрица из миноров 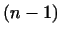 -го порядка
матрицы -го порядка
матрицы
 , а , а
 --
определитель матрицы --
определитель матрицы
 , т.е.
характеристический многочлен матрицы , т.е.
характеристический многочлен матрицы
 . Отсюда . Отсюда
 Так как элементами матрицы
Так как элементами матрицы
 являются
миноры матрицы являются
миноры матрицы
 , т.е. многочлены
степени не выше , т.е. многочлены
степени не выше  относительно относительно 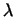 , то согласно доказанной
лемме , то согласно доказанной
лемме
 и теорема доказана.
и теорема доказана.
Заметим, что если у характеристического многочлена
матрицы
 нет кратных корней, то не существует
многочлена степени ниже нет кратных корней, то не существует
многочлена степени ниже  , обращающегося в нуль при подстановке в
него матрицы , обращающегося в нуль при подстановке в
него матрицы
 (см. следующее упражнение). (см. следующее упражнение).
Упражнение
Пусть
 -- диагональная матрица вида -- диагональная матрица вида
![$\displaystyle \arraycolsep2pt
\boldsymbol{A}=
\begin{pmatrix}
\lambda_1&0&\dots...
...\lambda_2&\dots&0\\
\hdotsfor[1.5]{4}\\
0&0&\dots&\lambda_n
\end{pmatrix},
$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img332.gif) где все числа
где все числа 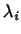 различны. Найти многочлен различны. Найти многочлен  возможно
более низкой степени, для которого возможно
более низкой степени, для которого
 . (См. пример
в §9, п.3.) . (См. пример
в §9, п.3.)





Next: 11 линейное преобразование, сопряженное
Previous: 9 линейные преобразования и
Vadim Yu. Radionov
2000-08-30
Посмотреть комментарии[2]
|

