Научная Сеть >> Курс лекций И.М.Гельфанда по линейной алгебре

Наука >> Математика >> Алгебра, математическая логика и теория чисел | Курсы лекций

Посмотреть комментарии[2]

Добавить новое сообщение

Next: 6 приведение к сумме Up: 1 n-мерное пространство. Линейные Previous: 4 билинейные и квадратичные

5 Приведение квадратичной формы к сумме квадратов

Мы знаем уже, что выражение квадратичной формы через координаты вектора зависит от выбора базиса. В этом параграфе будет показано, как привести квадратичную форму к сумме квадратов, т.е. выбрать такой базис (систему координат), в котором квадратичная форма имеет простой вид

$\displaystyle A(x; x)=\lambda_1\xi_1^2+\lambda_2\xi_2^2+\ldots+ \lambda_n\xi_n^2.$

(1)

Пусть в некотором базисе $f_1, f_2, \dots, f_n$ имеем равенство

$\displaystyle A(x,x)=\sum_{i,k=1}^n a_{ik}\eta_i\eta_k,$

(2)

где $\eta_1, \eta_2, \dots, \eta_n$ -- координаты вектора

в этом базисе. Будем постепенно преобразовывать базис так, чтобы в формуле (2) пропадали произведения координат с различными индексами. Так как каждому преобразованию базиса отвечает определенное преобразование координат (см. 1, п.6) и обратно, то мы можем писать формулы преобразования координат.

Для приведения формы к сумме квадратов нам нужно будет, чтобы хоть один из коэффициентов $a_{kk}$ (коэффициент при $\eta_k^2$ ) был отличен от нуля. Этого всегда можно добиться. Действительно, предположим, что форма , не равная тождественно нулю, не содержит ни одного квадрата переменного; тогда она содержит хотя бы одно произведение, например, $2a_{12}\eta_1\eta_2$ . Заменим координаты $\eta_1$ и $\eta_2$ по формулам

$\begin{displaymath} \begin{aligned} \eta_1&=\eta'_1+\eta'_2,\\ \eta_2&=\eta'_1-\eta'_2, \end{aligned}\end{displaymath}$

не изменяя остальных переменных. При этом преобразовании член $2a_{12}\eta_1\eta_2$ перейдет в $2a_{12}(\eta_1^{\prime2}-\eta_2^{\prime2})$ , и так как, по предположению, $a_{11}=a_{22}=0$ , то он ни с чем не может сократиться, т.е. коэффициент при $\eta_1^{\prime2}$ отличен от нуля.

Будем теперь считать, что уже в формуле (2) коэффициент 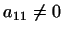$a_{11}\ne0$ 2.17. Выделим в нашей квадратичной форме члены, содержащие $\eta_1$ :

$\displaystyle a_{11}\eta_1^2+2a_{12}\eta_1\eta_2+\ldots+2a_{1n}\eta_1\eta_n.$

Дополним эту сумму до полного квадрата, т.е. запишем ее в виде

$\displaystyle a_{11}\eta_1^2+2a_{12}\eta_1\eta_2+\ldots+2a_{1n}\eta_1\eta_n =\frac{1}{a_{11}}(a_{11}\eta_1+\ldots+a_{1n}\eta_n)^2-B,$

(3)

где через

мы обозначили члены, содержащие лишь квадраты и попарные произведения членов $a_{12}\eta_2, \dots,a_{1n}\eta_n$ . После подстановки выражения (3) в (2) рассматриваемая квадратичная форма примет вид

$\displaystyle A(x; x)=\frac{1}{a_{11}}(a_{11}\eta_1+ \ldots+a_{1n}\eta_n)^2+\dots,$

где невыписанные члены содержат только переменные $\eta_2, \dots, \eta_n$ .

Положим

$\begin{displaymath} \begin{aligned} \eta^*_1&={}&a_{11}\eta_1+a_{12}& \eta_2+\ld... ...aders\hbox{ . }\hfil\\ \eta^*_n&=&&&\eta_n{.} \end{aligned}\end{displaymath}$

Тогда квадратичная форма примет вид

$\displaystyle A(x;x)=\frac{1}{a_{11}}\eta_1^{*2}+ \sum_{i,k=2}^na_{ik}^*\eta^*_i\eta^*_k.$

Выражение $\sum\limits_{i,k=1}^na_{ik}^*\eta^*_i\eta^*_k$ вполне аналогично правой части формулы (2) с той только разницей, что оно не содержит первой координаты. Предположим, что коэффициент $a^*_{22}\neq0$ (этого, как мы видели, всегда можно добиться простыми вспомогательными преобразованиями). Тогда можно произвести новое, аналогичное первому, преобразование переменных по формулам

$\begin{displaymath} \begin{aligned} \eta_1^{**}={}&\eta_1^*, &\\ \eta^{**}_2=... ...\hbox{ . }\hfil\\ \eta^{**}_n={}&&&&\eta_n^*. \end{aligned}\end{displaymath}$

В новых переменных форма примет вид

$\displaystyle A(x; x)=\frac{1}{a_{11}}\eta_1^{**2}+\frac{1}{a_{22}^*}\eta_2^{**2}+ \sum_{i,k=3}^na_{ik}^{**}\eta^{**}_i\eta^{**}_k.$

Продолжая этот процесс, мы после конечного числа шагов придем к переменным $\xi_1, \xi_2, \dots, \xi_n$ , в которых форма

будет иметь вид

$\displaystyle A(x; x)=\lambda_1\xi_1^2+\lambda_2\xi_2^2+\ldots+ \lambda_m\xi_m^2,$

причем $m\leqslant n$ .

Мы предоставляем читателю выписать преобразование базиса, отвечающее каждому из произведенных преобразований координат (см. п. 6 1), и убедиться, что наши преобразования действительно переводят базис снова в базис, т.е. что полученные из базиса в результате преобразования векторы снова линейно независимы.

Полагая в случае , что $\lambda_{m+1}=\ldots=\lambda_n=0$ , мы приходим, таким образом, к следующей теореме:

Теорема Пусть в -мерном пространстве задана произвольная квадратичная форма . Тогда в существует базис $e_1, e_2, \dots, e_n$ , в котором эта квадратичная форма имеет вид

$\displaystyle A(x; x)=\lambda_1\xi_1^2+\lambda_2\xi_2^2+\ldots+ \lambda_n\xi_n^2,$

где $\xi_1, \xi_2, \dots, \xi_n$ -- координаты вектора

в базисе $e_1, e_2, \dots, e_n$ .

Приведем пример приведения квадратичной формы к сумме квадратов по описанному методу. Пусть в трехмерном пространстве с некоторым базисом задана квадратичная форма

$\displaystyle A(x; x)=2\eta_1\eta_2+4\eta_1\eta_3-\eta_2^2-8\eta_3^2.$

Положим

$\begin{displaymath} \begin{aligned} \eta_1&=\eta'_2,\\ \eta_2&=\eta'_1,\\ \eta_3&=\eta'_3. \end{aligned}\end{displaymath}$

Тогда получим:

$\displaystyle A(x; x)=-{\eta'_1}^2+2\eta'_1\eta'_2+4 \eta'_2\eta'_3-8{\eta'_3}^2.$

Дальше, полагая

$\begin{displaymath} \begin{aligned} \eta_1^*=&-\eta'_1&{}+\eta'_2,\\ \eta_2^*=&&\eta'_2,\\ \eta_3^*=&&&\eta'_3, \end{aligned}\end{displaymath}$

мы получим новое выражение для квадратичной формы:

$\displaystyle A(x; x)=-{\eta_1^*}^2+{\eta_2^*}^2+4\eta_2^*\eta_3^* -8{\eta_3^*}^2.$

Преобразование

$\begin{displaymath} \begin{aligned} \xi_1&=&\eta_1^*,\\ \xi_2&=&&\eta_2^*+2&\eta_3^*{,}\\ \xi_3&=&&&\eta_3^*\hphantom{,} \end{aligned}\end{displaymath}$

выделит из нашей квадратичной формы еще один полный квадрат, после чего форма примет канонический вид:

$\displaystyle A(x; x)=-\xi_1^2+\xi_2^2-12\xi_3^2.$

Имея формулы, выражающие $\eta_1^*, \eta_2^*, \dots, \eta_n^*$ через $\eta_1, \eta_2, \dots, \eta_n$ , затем $\eta_1^{**}, \dots, \eta_n^{**}$ через $\eta_1^*, \eta_2^*, \dots, \eta_n^*$ и т.д., мы можем получить выражение координат $\xi_1, \xi_2, \dots, \xi_n$ через первоначальные координаты $\eta_1, \eta_2, \dots, \eta_n$ :

$\begin{displaymath} \begin{aligned} \xi_1&=c_{11}\eta_1+c_{12}\eta_2+\ldots+c_{1... ...n&=c_{n1}\eta_1+c_{n2}\eta_2+\ldots+c_{nn}\eta_n. \end{aligned}\end{displaymath}$

Так, в приведенном выше примере эти формулы имеют вид

$\begin{displaymath} \begin{aligned} \xi_1&=\eta_1-\eta_2,\\ \xi_2&=\eta_1 &{}+2&\eta_3,\\ \xi_3&=&&\eta_3. \end{aligned}\end{displaymath}$

Вспоминая ( 1, п.6), что матрица, дающая преобразование координат, является обратной и транспонированной к матрице преобразования базиса, мы можем выразить векторы нового базиса $e_1, e_2, \dots, e_n$ через векторы старого базиса $f_1, f_2, \dots, f_n$ :

$\begin{displaymath} \begin{aligned} e_1&=d_{11}f_1+d_{12}f_2+\ldots+d_{1n}f_n,\\... ...il\\ e_n&=d_{n1}f_1+d_{n2}f_2+\ldots+d_{nn}f_n. \end{aligned}\end{displaymath}$

Если в процессе приведения нам ни разу не приходилось производить преобразования, меняющего сразу две координаты (такое преобразование, как мы помним, приходится совершать, когда в преобразуемой форме отсутствуют квадраты координат, либо если приходилось менять нумерацию), то формулы преобразования имеют вид

$\begin{displaymath} \begin{aligned} \xi_1={}&c_{11}\eta_1+{}&c_{12}\eta_2+\ldots... ...ers\hbox{ . }\hfil\\ \xi_n={}&&&c_{nn}\eta_n, \end{aligned}\end{displaymath}$

т.е. матрица преобразования является так называемой треугольной матрицей. Легко проверить, что матрица преобразования базиса будет в этом случае также треугольной матрицей вида

$\begin{displaymath} \begin{aligned} e_1&=d_{11}f_1,\\ e_2&=d_{21}f_1+d_{22}f_2... ...ad\\ e_n&=d_{n1}f_1+d_{n2}f_2+\ldots+d_{nn}f_n. \end{aligned}\end{displaymath}$

Здесь $d_{\alpha\beta}$ -- алгебраическое дополнение элемента $c_{\alpha\beta}$ матрицы $\Vert c_{ik}\Vert$ , деленное на определитель этой матрицы.

Next: 6 приведение к сумме Up: 1 n-мерное пространство. Линейные Previous: 4 билинейные и квадратичные Vadim Yu. Radionov
2000-08-30

МЦНМО

Посмотреть комментарии[2]