... 2.1
Запись
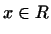 означает, что означает, что 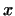 принадлежит принадлежит 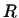 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... соответствие 2.2
Соответствие, установленное между элементами двух множеств .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... соответствие 2.2
Соответствие, установленное между элементами двух множеств 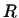 и и
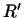 , называется взаимно однозначным, если: , называется взаимно однозначным, если:
1 каждому элементу из каждому элементу из 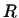 соответствует один и только один
элемент из соответствует один и только один
элемент из 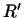 , ,
2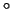 каждый элемент из каждый элемент из 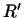 соответствует при этом одному
и только одному элементу из соответствует при этом одному
и только одному элементу из 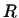 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... нуля 2.3
Если бы определитель матрицы .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... нуля 2.3
Если бы определитель матрицы
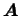 был равен нулю, то
векторы был равен нулю, то
векторы
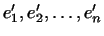 были бы линейно зависимы.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... геометрии 2.4
Можно было бы, конечно, определить евклидово пространство иначе, чем
в п.1, введя аксиоматически понятия длины вектора и
угла между векторами (а не скалярное произведение). Однако
соответствующая система аксиом была бы более сложной.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
Коши-Буняковского 2.5
В примере 1 п.1 этого параграфа нет надобности
доказывать это неравенство. Действительно, там в силу принятого в
векторном исчислении определения скалярного произведения величина были бы линейно зависимы.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... геометрии 2.4
Можно было бы, конечно, определить евклидово пространство иначе, чем
в п.1, введя аксиоматически понятия длины вектора и
угла между векторами (а не скалярное произведение). Однако
соответствующая система аксиом была бы более сложной.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
Коши-Буняковского 2.5
В примере 1 п.1 этого параграфа нет надобности
доказывать это неравенство. Действительно, там в силу принятого в
векторном исчислении определения скалярного произведения величина
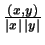 есть косинус некоторого уже заранее
определенного угла между векторами и поэтому она по абсолютной
величине не превосходит 1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... есть косинус некоторого уже заранее
определенного угла между векторами и поэтому она по абсолютной
величине не превосходит 1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...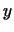 2.6
Мы будем обозначать одной и той же буквой вектор и точку, являющуюся
его концом (векторы мы проводим из начала координат,
см. стр. 2.6
Мы будем обозначать одной и той же буквой вектор и точку, являющуюся
его концом (векторы мы проводим из начала координат,
см. стр.![[*]](http://images.nature.web.ru/nature/2000/10/02/0001151602/crossref.png) ).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... равноправны 2.7
Точный смысл этого утверждения таков. Если внимательно посмотреть
приведенное в 1 доказательство изоморфизма аффинных
пространств, то легко заметить, что там доказано несколько больше, чем
сформулировано, а именно, доказано, что между двумя ).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... равноправны 2.7
Точный смысл этого утверждения таков. Если внимательно посмотреть
приведенное в 1 доказательство изоморфизма аффинных
пространств, то легко заметить, что там доказано несколько больше, чем
сформулировано, а именно, доказано, что между двумя 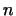 -мерными
пространствами можно установить изоморфное соответствие так, чтобы
заданный базис одного пространства перешел в заданный базис другого
пространства. В частности, если в -мерными
пространствами можно установить изоморфное соответствие так, чтобы
заданный базис одного пространства перешел в заданный базис другого
пространства. В частности, если в 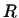 заданы два базиса заданы два базиса
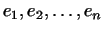 и и
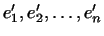 , то существует изоморфное
отображение пространства , то существует изоморфное
отображение пространства 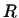 на себя, при котором первый базис
переходит во второй.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...P2.8
Этот пункт можно при первом чтении пропустить.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... 2.9
Для случая, когда на себя, при котором первый базис
переходит во второй.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...P2.8
Этот пункт можно при первом чтении пропустить.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... 2.9
Для случая, когда 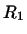 есть плоскость, эта теорема в элементарной
геометрии называется теоремой о двух перпендикулярах.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... 2.10
Размерность самого пространства есть плоскость, эта теорема в элементарной
геометрии называется теоремой о двух перпендикулярах.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... 2.10
Размерность самого пространства 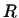 для нас несущественна. Оно может
быть даже бесконечномерным.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... 2.11
Мы предполагаем,что ранг матрицы системы (13) равен для нас несущественна. Оно может
быть даже бесконечномерным.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... 2.11
Мы предполагаем,что ранг матрицы системы (13) равен 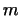 и,
следовательно, векторы и,
следовательно, векторы
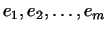 линейно независимы.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
пространстве 2.12
Геометрической теоремой мы будем называть утверждение о векторах,
которое может быть сформулировано в терминах сложения векторов,
умножения их на числа и скалярного произведения.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... означает 2.13
Произведение двух матриц определяется, как известно, так: элемент
произведения матриц, стоящий на пересечении линейно независимы.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
пространстве 2.12
Геометрической теоремой мы будем называть утверждение о векторах,
которое может быть сформулировано в терминах сложения векторов,
умножения их на числа и скалярного произведения.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... означает 2.13
Произведение двух матриц определяется, как известно, так: элемент
произведения матриц, стоящий на пересечении 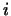 -й строки и -й строки и 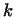 -го
столбца, равен сумме произведений элементов -го
столбца, равен сумме произведений элементов 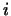 -й строки первой
матрицы на соответствующие элементы -й строки первой
матрицы на соответствующие элементы 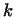 -го столбца второй матрицы.
Удобнее это правило записывать в виде формулы -го столбца второй матрицы.
Удобнее это правило записывать в виде формулы
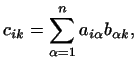 где
где
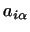 -- элементы первой матрицы, а -- элементы первой матрицы, а
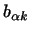 -- элементы второй матрицы. Отсюда, применяя это правило
дважды, можно получить, что произведение трех матриц вычисляется
так: если
-- элементы второй матрицы. Отсюда, применяя это правило
дважды, можно получить, что произведение трех матриц вычисляется
так: если
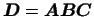 , то , то
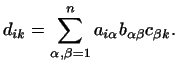 Если
Если
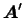 -- матрица, транспонированная к матрице -- матрица, транспонированная к матрице
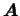 , то элементы матрицы , то элементы матрицы
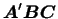 имеют вид
имеют вид
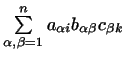 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... формой 2.14
Функция .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... формой 2.14
Функция 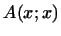 , полученная из произвольной (не обязательно
симметрической) билинейной формы , полученная из произвольной (не обязательно
симметрической) билинейной формы 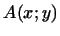 , может быть получена и из
симметрической билинейной формой. Действительно, пусть , может быть получена и из
симметрической билинейной формой. Действительно, пусть 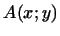 --
произвольная билинейная форма; тогда --
произвольная билинейная форма; тогда
![$\displaystyle A_1(x; y)=\frac{1}{2}[A(x; y)+A(y; x)]
$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch1img556.gif) есть снова билинейная форма и притом, как можно видеть,
симметрическая. Но
есть снова билинейная форма и притом, как можно видеть,
симметрическая. Но
![$\displaystyle A_1(x; x)=\frac{1}{2}[A(x; x)+A(x; x)]=A(x; x),
$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch1img557.gif) т.е.
т.е. 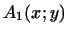 приводит нас (при приводит нас (при 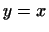 ) к той же квадратичной
форме, что и ) к той же квадратичной
форме, что и 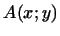 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
соответствующей 2.15
Мы уже доказали, что билинейная форма .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
соответствующей 2.15
Мы уже доказали, что билинейная форма 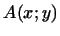 однозначно
определяется своей квадратичной формой однозначно
определяется своей квадратичной формой 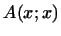 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
произведением2.16
Выше оно обозначалось .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
произведением2.16
Выше оно обозначалось  , а не , а не 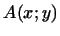 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... 2.17
Если .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... 2.17
Если 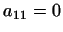 , но отличен от нуля коэффициент при квадрате
какой-нибудь другой координаты, то к рассматриваемому случаю можно
прийти, иначе занумеровав векторы , но отличен от нуля коэффициент при квадрате
какой-нибудь другой координаты, то к рассматриваемому случаю можно
прийти, иначе занумеровав векторы
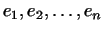 , что также
является некоторым преобразованием этого базиса.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... нуля2.18
Можно показать, что это требование равносильно тому, что при
приведении квадратичной формы к сумме квадратов по методу, описанному
в 5, , что также
является некоторым преобразованием этого базиса.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... нуля2.18
Можно показать, что это требование равносильно тому, что при
приведении квадратичной формы к сумме квадратов по методу, описанному
в 5,
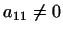 , ,
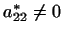 и т.д.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
2.19
Выкладка сильно усложнилась бы, если бы мы заменили и т.д.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
2.19
Выкладка сильно усложнилась бы, если бы мы заменили
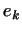 его выражением через его выражением через 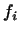 и на первом, и на втором месте.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... и на первом, и на втором месте.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
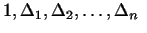 2.20
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... миноры 2.21
Главными минорами называются те, при составлении которых выделяются
столбцы с теми же номерами, что и строки.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... пространстве 2.22
Для нас, конечно, несущественно, что размерность
пространства равна 2.20
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... миноры 2.21
Главными минорами называются те, при составлении которых выделяются
столбцы с теми же номерами, что и строки.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... пространстве 2.22
Для нас, конечно, несущественно, что размерность
пространства равна 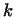 . В действительности пространство . В действительности пространство 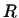 может
иметь произвольное (даже бесконечное) число измерений, поскольку
наши рассуждения могут быть отнесены к подпространству,
порожденному векторами может
иметь произвольное (даже бесконечное) число измерений, поскольку
наши рассуждения могут быть отнесены к подпространству,
порожденному векторами
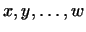 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... вид 2.23
Коэффициенты .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... вид 2.23
Коэффициенты 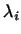 в формуле (1) можно, как
мы знаем, сделать равными в формуле (1) можно, как
мы знаем, сделать равными 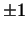 или 0. Те члены, для которых или 0. Те члены, для которых
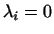 , мы в формулах (2) и (3) опускаем.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
2.24
В формуле (5) нельзя вместо знака , мы в формулах (2) и (3) опускаем.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
2.24
В формуле (5) нельзя вместо знака 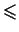 поставить знак поставить знак
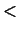 , так как, хотя среди чисел , так как, хотя среди чисел
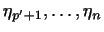 есть
отличные от нуля, но возможно, что есть
отличные от нуля, но возможно, что
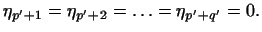 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... формы 2.25
Пользуясь тем известным из теории матриц фактом, что ранг матрицы не
меняется при умножении ее на любую неособенную матрицу, этот результат
можно получить и непосредственно из выведенной в 4
формулы преобразования матрицы билинейной формы при изменении базиса
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... формы 2.25
Пользуясь тем известным из теории матриц фактом, что ранг матрицы не
меняется при умножении ее на любую неособенную матрицу, этот результат
можно получить и непосредственно из выведенной в 4
формулы преобразования матрицы билинейной формы при изменении базиса
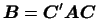 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... формой 2.26
В отличие от определенных в 4 форм в вещественном
пространстве, для которых соответствующее утверждение справедливо лишь
для симметрических билинейных форм.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... тождество 2.27
Читатель должен помнить, что .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... формой 2.26
В отличие от определенных в 4 форм в вещественном
пространстве, для которых соответствующее утверждение справедливо лишь
для симметрических билинейных форм.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... тождество 2.27
Читатель должен помнить, что
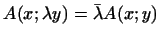 и,
следовательно, в частности, и,
следовательно, в частности,
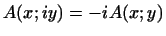 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Посмотреть комментарии[2]
|

