Основной интерес для нас представляет сейчас, естественно, формула (3): она позволяет "пересчитать" ускорение точки из 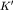 -системы в K-систему, а значит, и наоборот - из K-системы в -системы в K-систему, а значит, и наоборот - из K-системы в 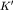 -систему. Благодаря этому обстоятельству, уравнение движения точки, записанное в K-системе (оно будет содержать ее "абсолютное" ускорение -систему. Благодаря этому обстоятельству, уравнение движения точки, записанное в K-системе (оно будет содержать ее "абсолютное" ускорение 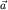 ), можно будет "приспособить" для записи (и интерпретации) в ), можно будет "приспособить" для записи (и интерпретации) в 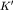 -системе. Но об этом далее. Сейчас же, чтобы выявить удобные классификационные признаки, по которым можно различать разновидности сил инерции, выделим вклады в ускорение -системе. Но об этом далее. Сейчас же, чтобы выявить удобные классификационные признаки, по которым можно различать разновидности сил инерции, выделим вклады в ускорение 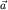 в соответствии с тем, что точка участвует в двух движениях - "переносном" и "относительном". в соответствии с тем, что точка участвует в двух движениях - "переносном" и "относительном".
Сумма первых трех вкладов в 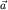 - это, по определению, "переносное" ускорение точки: - это, по определению, "переносное" ускорение точки:
![$\vec {a}_{per} \equiv \vec A + \left[ \vec {\omega} \left[ \vec {\omega} \vec {r'} \right] \right]+\left[ \vec {\beta} \vec {r'}\right]$.](http://images.nature.web.ru/nature/2001/01/27/0001159981/tex/formula42.gif) | (4) |
"Переносное" ускорение 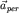 не содержит никаких индивидуальных характеристик движения самой рассматриваемой точки. Ведь, действительно, радиус-вектор не содержит никаких индивидуальных характеристик движения самой рассматриваемой точки. Ведь, действительно, радиус-вектор 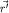 , как и все другие величины в (4) - , как и все другие величины в (4) - 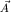 , , 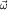 , , 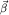 , не является индивидуальной характеристикой ее движения: это всего лишь радиус-вектор занимаемого ею места в , не является индивидуальной характеристикой ее движения: это всего лишь радиус-вектор занимаемого ею места в 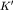 -системе. Если в этом месте нет никакой материальной точки, то оно, это место, все равно будет "переноситься" -системе. Если в этом месте нет никакой материальной точки, то оно, это место, все равно будет "переноситься" 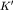 -системой относительно K-системы с этим ускорением -системой относительно K-системы с этим ускорением 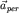 . Если же в этом месте, задаваемом радиус-вектором . Если же в этом месте, задаваемом радиус-вектором 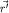 , есть еще и материальная точка, то и она, согласно (3), тоже будет иметь вклад , есть еще и материальная точка, то и она, согласно (3), тоже будет иметь вклад 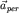 в ее суммарное ускорение в ее суммарное ускорение 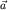 в K-системе. в K-системе.
Поскольку ускорение 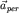 содержит три различных вклада, то, значит, есть три различных причины его возникновения (здесь пока имеется в виду кинематическая, т.е. описательная, сторона дела). Первая причина - это наличие ускорения содержит три различных вклада, то, значит, есть три различных причины его возникновения (здесь пока имеется в виду кинематическая, т.е. описательная, сторона дела). Первая причина - это наличие ускорения  у всех точек у всех точек  -системы в ее поступательном движении (со скоростью -системы в ее поступательном движении (со скоростью 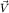 ) относительно K-системы; вторая - вращение ) относительно K-системы; вторая - вращение 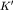 -системы, как "целого", относительно мгновенной оси, проходящей через ее начало -системы, как "целого", относительно мгновенной оси, проходящей через ее начало 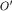 , с угловой скоростью , с угловой скоростью 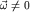 ; третья - наличие углового ускорения ; третья - наличие углового ускорения 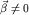 у этого вращательного движения. K-наблюдатель "увидит" все эти три вклада в ускорение у этого вращательного движения. K-наблюдатель "увидит" все эти три вклада в ускорение 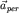 : он может измерить их с помощью линейки и часов. Что же касается : он может измерить их с помощью линейки и часов. Что же касается 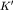 -наблюдателя, он "не увидит" ни одного из этих трех вкладов в -наблюдателя, он "не увидит" ни одного из этих трех вкладов в 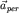 : ведь все точки : ведь все точки 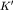 -системы покоятся относительно -системы покоятся относительно 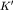 -системы. -системы.
"Не увидит" 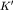 -наблюдатель и второго основного вклада в суммарное ускорение точки -наблюдатель и второго основного вклада в суммарное ускорение точки 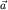 - так называемое кориолисово ускорение - так называемое кориолисово ускорение
![$\vec {a}_{kor} \equiv 2\left[ \vec {\omega} \vec {v'} \right]$.](http://images.nature.web.ru/nature/2001/01/27/0001159981/tex/formula46.gif) | (5) |
Причина проста: 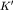 -наблюдатель может "увидеть" в своей системе отсчета лишь одно-единственное ускорение из всех перечисленных выше - "относительное" ускорение -наблюдатель может "увидеть" в своей системе отсчета лишь одно-единственное ускорение из всех перечисленных выше - "относительное" ускорение 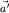 . Это - третий (и последний из основных) вклад в "абсолютное" ускорение точки в K-системе, так что, согласно (3)-(5), . Это - третий (и последний из основных) вклад в "абсолютное" ускорение точки в K-системе, так что, согласно (3)-(5),
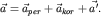 | (6) |
Теперь наша задача - записать уравнение движения для некоторой материальной точки массы m. Поскольку мы только еще собираемся ввести в рассмотрение силы инерции, у нас нет иного способа записать уравнение движения точки, кроме традиционного - в инерциальной системе отсчета, где действуют только "обычные" силы. Таким образом, переходя от кинематики движения точки к динамическим аспектам ее движения, мы должны вначале выбрать инерциальную систему отсчета. Допустим, именно такой, инерциальной, является K-система.  -система будет в таком случае неинерциальной - для этого достаточно, чтобы было выполнено любое из трех условий: -система будет в таком случае неинерциальной - для этого достаточно, чтобы было выполнено любое из трех условий: 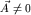 , , 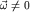 , , 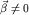 . .
В соответствии со вторым законом Ньютона, уравнение движения точки в K-системе представится в виде:
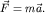 | (7) |
Здесь 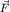 - равнодействующая всех "обычных" сил, действующих на материальную точку массы m. - равнодействующая всех "обычных" сил, действующих на материальную точку массы m.
Вот теперь у нас есть возможность "приспособить" уравнение движения, записанное в инерциальной системе отсчета, для записи его в неинерциальной системе. С этой целью перепишем уравнение движения (7), воспользовавшись формулой сложения ускорений (6):
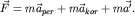 | (8) |
Если "конструировать" уравнение движения материальной точки в 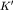 -системе по аналогии с (7) на основе эквивалентного ему равенства (8), надо оставить в правой части этого нового уравнения движения только лишь слагаемое -системе по аналогии с (7) на основе эквивалентного ему равенства (8), надо оставить в правой части этого нового уравнения движения только лишь слагаемое 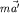 : :
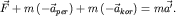 | (9) |
Так как 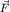 - равнодействующая всех "обычных" сил, то, следовательно, два других слагаемых в левой части уравнения (9) - "необычные" силы? Да, это и есть силы инерции: так можно трактовать эти два новых слагаемых, появившихся в уравнении движения при переходе из инерциальной системы отсчета K в неинерциальную - равнодействующая всех "обычных" сил, то, следовательно, два других слагаемых в левой части уравнения (9) - "необычные" силы? Да, это и есть силы инерции: так можно трактовать эти два новых слагаемых, появившихся в уравнении движения при переходе из инерциальной системы отсчета K в неинерциальную 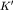 -систему. -систему.
Назад | Вперед
Посмотреть комментарии[1]
|

