Едва ли стоит доказывать, что тема "Силы инерции" - одна из самых трудных в разделе "Механика" общего курса физики. Чтобы убедиться в этом, достаточно вспомнить один лишь тот факт, что силы инерции, при первом серьезном знакомстве с ними, воспринимаются как весьма непривычные по сравнению с так называемыми "обычными" силами - такими как силы тяготения, упругости, трения. Как помочь студенту-первокурснику в освоении этой темы?
В этом стремлении помочь многое зависит от двух немаловажных обстоятельств: от способа изложения материала и от подбора примеров и задач, поясняющих основные идеи. Под способом изложения здесь подразумевается прежде всего логическая последовательность утверждений, которая имеет своей целью обоснование концепции сил инерции в целом. Логическая стройность изложения материала достигается в том случае, когда вводимые новые понятия приводятся в систему на основе удобных классификационных признаков. В данном случае это относится в первую очередь к самим силам инерции, а точнее - к их разновидностям. Что же касается примеров и задач, их отбор должен быть подчинен фактически той же главной цели: они должны помочь выявить все основные особенности сил инерции, причем непременно в сравнении с "обычными" силами.
Тема "Силы инерции" излагается довольно подробно во многих известных курсах механики (см., например, [Фриш С.Э., 1953, Хайкин С.Э., 1963, Стрелков С.П., 1965, Киттель Ч., 1971, Сивухин Д.В., 1974, Матвеев А.Н., 1986]). Вместе с тем практически ни в одном из известных руководств по этому разделу общего курса физики нет ясного ответа на вопрос: сколько всего имеется разновидностей сил инерции? Исключение составляет, пожалуй, лишь книга [Сивухин Д.В., 1974], где вопрос о разновидностях сил инерции рассматривается на системной основе.
В данной статье предлагается несколько иной, нежели в [Сивухин Д.В., 1974], способ введения сил инерции. Вносимое изменение имеет своей целью сделать формально одинаковой процедуру введения всех без исключения разновидностей сил инерции.1
Силы инерции удобно ввести в рассмотрение, воспользовавшись "готовыми" формулами кинематики. Следуя сложившейся традиции, обратимся вначале к конкретному случаю, когда материальная точка участвует сразу в двух движениях. Во-первых, она движется относительно некоторой системы отсчета 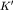 , имея в этой системе радиус-вектор , имея в этой системе радиус-вектор 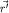 , скорость , скорость  и ускорение и ускорение 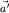 , соответствующие каждому данному моменту времени t ("относительное" движение). Кроме того, эта точка участвует еще и во втором движении - вместе с системой , соответствующие каждому данному моменту времени t ("относительное" движение). Кроме того, эта точка участвует еще и во втором движении - вместе с системой 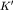 , которая "переносит" ее относительно системы отсчета K ("переносное" движение). , которая "переносит" ее относительно системы отсчета K ("переносное" движение).
Задача о сложении двух движений точки, "относительного" и "переносного", состоит в том, чтобы "пересчитать" кинематические характеристики ее движения в 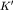 -системе -системе 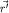 , ,  , , 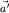 в аналогичные характеристики ее движения в K-системе в аналогичные характеристики ее движения в K-системе  , ,  , , 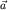 . В итоговые формулы, наряду с названными шестью векторными величинами, должны войти, очевидно, и "параметры задачи" - кинематические характеристики самого "переносного" движения. . В итоговые формулы, наряду с названными шестью векторными величинами, должны войти, очевидно, и "параметры задачи" - кинематические характеристики самого "переносного" движения.
Помня о главном предмете разговора (он вынесен в заголовок статьи), условимся рассматривать достаточно общий случай "переносного" движения: это позволит нам не упустить из виду ни одной из разновидностей сил инерции. Будем считать, что начало отсчета 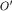 системы системы 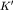 задается в K-системе радиус-вектором задается в K-системе радиус-вектором  и что оно имеет (в той же K-системе) скорость и что оно имеет (в той же K-системе) скорость  и ускорение и ускорение  . Сама . Сама 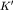 -система, как "целое", пусть при этом еще и вращается (рис. 1) - вокруг мгновенной оси, проходящей через ее начало отсчета -система, как "целое", пусть при этом еще и вращается (рис. 1) - вокруг мгновенной оси, проходящей через ее начало отсчета 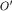 , с угловой скоростью , с угловой скоростью 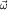 и угловым ускорением и угловым ускорением  . В роли "параметров задачи" выступают, таким образом, четыре векторных величины: . В роли "параметров задачи" выступают, таким образом, четыре векторных величины:  , , 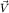 , , 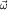 , , 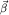 . .

Рис.1.
Результатом решения задачи о сложении двух движений точки будут, как известно, следующие итоговые формулы (подробности см. в [ Сивухин Д.В., 1974, Хайкин С.Э., 1963,]):
 | (1) |
![$\vec v = \vec V + \left[ \vec {\omega} \vec {r'} \right] + \vec {v'}$,](http://images.nature.web.ru/nature/2001/01/27/0001159981/tex/formula39.gif) | (2) |
![$\vec {a} = \vec {A} + \left[ \vec {\omega} \left[ \vec {\omega} \vec {r'} \right] \right] + \left[ \vec {\beta} \vec {r'} \right] + 2 \left[ \vec {\omega} \vec {v'} \right] + \vec {a'}$.](http://images.nature.web.ru/nature/2001/01/27/0001159981/tex/formula40.gif) | (3) |
Назад | Вперед
Посмотреть комментарии[1]
|

