<< 1.3 Сферически-симметричные поля тяг...
| Оглавление |
1.5 Давление газа ... >>
Мы видели, что энергия гравитационного взаимодействия 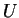 для двух масс для двух масс  и и  равна
равна
 . На случай . На случай 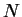 точечных масс выражение для точечных масс выражение для 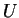 обобщается
следующим образом: обобщается
следующим образом:
 При таком определении
При таком определении 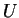 каждая пара каждая пара  входит в сумму только один раз.
Введем величину входит в сумму только один раз.
Введем величину
 что, очевидно, представляет собой гравитационный потенциал, создаваемый в
что, очевидно, представляет собой гравитационный потенциал, создаваемый в 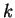 -той
точке всеми остальными массами. Теперь для -той
точке всеми остальными массами. Теперь для 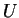 можно написать можно написать
 Коэффициент
Коэффициент
 появился вследствие того, что каждая пара точек входит в
сумму два раза. Это выражение легко обобщить на случай непрерывной среды: появился вследствие того, что каждая пара точек входит в
сумму два раза. Это выражение легко обобщить на случай непрерывной среды:
 (по определению
(по определению
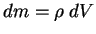 ). ).
Для точечных масс необходимо было отбрасывать энергию самодействия, оговаривая
правило суммирования. В сплошной среде самодействие не учитывается автоматически.
По порядку величины
 , и самодействие элемента , и самодействие элемента 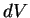 есть есть
 , т.е. величина более высокого порядка, чем
энергия взаимодействия с остальными массами, которая , т.е. величина более высокого порядка, чем
энергия взаимодействия с остальными массами, которая
 . .
Используем теперь выражение  для сферически-симметричного распределения для сферически-симметричного распределения
 и вычислим гравитационную энергию. Имеем: и вычислим гравитационную энергию. Имеем:
 |
(1.3) |
Это выражение можно значительно упростить. Введем вспомогательную функцию
 . Очевидно, . Очевидно,  и кроме этого и кроме этого
 Имеем также
Имеем также  . .
Таким образом, интеграл от первого члена в выражении (1.3) равен
интегралу от второго, и окончательно получим
 Это выражение проще получить иным путем, рассматривая, какую работу совершают
гравитационные силы при наращивании данной конфигурации последовательными
слоями. Пусть масса
Это выражение проще получить иным путем, рассматривая, какую работу совершают
гравитационные силы при наращивании данной конфигурации последовательными
слоями. Пусть масса 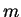 с радиусом с радиусом 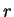 уже изготовлена. Прибавим к этой массе
новый сферический слой уже изготовлена. Прибавим к этой массе
новый сферический слой 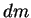 . Тогда совершенная работа, очевидно, равна . Тогда совершенная работа, очевидно, равна
 и т.д. В результате получим и т.д. В результате получим

<< 1.3 Сферически-симметричные поля тяг...
| Оглавление |
1.5 Давление газа ... >>
Посмотреть комментарии[2]
|

