<< 9.3 Сферически-симметричное поле ...
| Оглавление |
9.5 Устойчивость релятивистских ... >>
Рассмотрим некоторые общие свойства этих решений для равновесных релятивистских звезд.
Механическое равновесие соответствует минимуму энергии (т. е. массы) -- в общем
случае экстремуму при данном количестве барионов и данном распределении энтропии по
барионам. В частном случае холодного вещества энтропия везде равна нулю. Решение,
устойчивое относительно радиальных перемещений, при этом всегда безразлично относительно
конвекции.
1. Пусть дано некоторое распределение энтропии 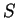 . В сферически-симметричном случае . В сферически-симметричном случае 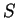 является функцией текущего числа барионов:
является функцией текущего числа барионов:

 -- лагранжева координата, поэтому при всех вариациях -- лагранжева координата, поэтому при всех вариациях  , в отличие от , в отличие от 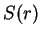 ,
всегда фиксирована. Состояние равновесия соответствует минимуму ,
всегда фиксирована. Состояние равновесия соответствует минимуму 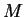 при данном при данном  при вариациях
при вариациях  (или (или  ). (Вопрос о конвективной устойчивости здесь не ставится.) ). (Вопрос о конвективной устойчивости здесь не ставится.)
2. Пусть звезда изэнтропична: 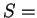 const. Можно и в этом случае действовать по-прежнему, т. е.
находить минимум const. Можно и в этом случае действовать по-прежнему, т. е.
находить минимум 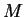 при вариациях при вариациях  и фиксированном и фиксированном 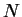 , но теперь проявляется еще
одна степень свободы: мы можем переставлять частицы между любыми слоями.
При перестановке энергия
не должна меняться (в первом порядке). Отсюда сразу получается условие на химический потенциал
вещества , но теперь проявляется еще
одна степень свободы: мы можем переставлять частицы между любыми слоями.
При перестановке энергия
не должна меняться (в первом порядке). Отсюда сразу получается условие на химический потенциал
вещества 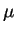 : :
 const const |
(9.7) |
по звезде.
Химпотенциал определяется как приращение энергии системы при добавлении единицы массы покоя:
 Такой вид выражения для
Такой вид выражения для 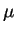 объясняется тем, что если внутрь звезды поместить элемент
массы объясняется тем, что если внутрь звезды поместить элемент
массы
 , то работа , то работа
 (работа по раздвиганию
окружающего вещества) (работа по раздвиганию
окружающего вещества)
 . Множитель . Множитель  играет роль
гравитационного потенциала (работа по перенесению барионов из бесконечности равна играет роль
гравитационного потенциала (работа по перенесению барионов из бесконечности равна
 ). Константу в (9.7) легко найти из условий на поверхности.
Там ). Константу в (9.7) легко найти из условий на поверхности.
Там

 Итак,
Итак,


|
| Рис. 58. |
Предположим, что мы хотим подсчитать, как изменится масса звезды 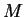 при изменении
числа барионов, т. е. при изменении при изменении
числа барионов, т. е. при изменении 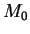 . Для этого нам нужно сравнить два близких,
но разных решения. Эти два решения различаются во всех точках. Но из принципа экстремума
ясно, что можно сначала добавить барионы на поверхности
(см. рис. 58). При этом,
во-первых, изменится масса . Для этого нам нужно сравнить два близких,
но разных решения. Эти два решения различаются во всех точках. Но из принципа экстремума
ясно, что можно сначала добавить барионы на поверхности
(см. рис. 58). При этом,
во-первых, изменится масса
 Во-вторых, это решение не равновесно. Поэтому звезда перестроится. Но изменение массы
при перестройке около равновесия имеет высший порядок малости, поэтому в первом порядке
масса и после перестройки та же
(см. разделы 1.7,
1.8). В результате имеем
Во-вторых, это решение не равновесно. Поэтому звезда перестроится. Но изменение массы
при перестройке около равновесия имеет высший порядок малости, поэтому в первом порядке
масса и после перестройки та же
(см. разделы 1.7,
1.8). В результате имеем


|
| Рис. 59. | Рис. 60. |
Следовательно,
 т. е. экстремумы кривых
т. е. экстремумы кривых 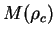 и и
 совпадают (рис. 59).
Интересно, что при
некоторой совпадают (рис. 59).
Интересно, что при
некоторой 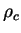 величина величина 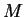 становится больше становится больше 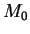 . Как это может получится, если . Как это может получится, если
 всегда меньше единицы? Все объясняется просто: кривая всегда меньше единицы? Все объясняется просто: кривая  не гладкая (рис. 60),
поэтому она может пересечь биссектрису не гладкая (рис. 60),
поэтому она может пересечь биссектрису  . .
<< 9.3 Сферически-симметричное поле ...
| Оглавление |
9.5 Устойчивость релятивистских ... >>
Посмотреть комментарии[2]
|

