<< 1.2 Векторное поле ускорений ...
| Оглавление |
1.4 Энергия гравитационного взаимодействия >>
Рассмотрим тонкий сферический слой с радиусом 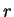 , толщиной , толщиной
 и
поверхностной плотностью и
поверхностной плотностью 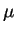 [г/см [г/см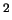 ]. Найдем силу притяжения со стороны сферы,
которая действует на пробную частицу единичной массы, помещенную в какой-либо точке ]. Найдем силу притяжения со стороны сферы,
которая действует на пробную частицу единичной массы, помещенную в какой-либо точке
 внутри сферы. Из рис.2
наглядно видно, что силы притяжения двух элементов
масс, вырезанных на сфере телесным углом внутри сферы. Из рис.2
наглядно видно, что силы притяжения двух элементов
масс, вырезанных на сфере телесным углом 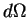 , одинаковы по величине и
противоположны по направлению. Более близкий к точке , одинаковы по величине и
противоположны по направлению. Более близкий к точке  элемент элемент  имеет
меньшую массу, и сила притяжения, создаваемая им в точке имеет
меньшую массу, и сила притяжения, создаваемая им в точке  , ,
 Так как правая часть этого выражения зависит лишь от величины телесного угла
Так как правая часть этого выражения зависит лишь от величины телесного угла
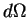 и и
 , которые одинаковы для , которые одинаковы для  и и  , то со стороны , то со стороны
 действует равная по величине сила действует равная по величине сила
 . Таким образом, любая пара
участков сферы внутри двойного конуса . Таким образом, любая пара
участков сферы внутри двойного конуса 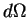 дает полную силу, равную нулю,
и пробная частица внутри сферы не испытывает силы и ускорения. Этот результат
остается в силе и для сферы конечной толщины ( дает полную силу, равную нулю,
и пробная частица внутри сферы не испытывает силы и ускорения. Этот результат
остается в силе и для сферы конечной толщины (
 ). ).
 |
| Рис. 2. | Рис. 3. |
Теперь расположим нашу пробную частицу вне сферы
(рис. 3). Сила, действующая на
частицу в этом случае, равна
 |
(1.2) |
и направлена к центру сферы. Здесь 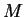 -- полная масса сферической оболочки, -- полная масса сферической оболочки,
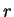 -- расстояние от
-- расстояние от  до центра сферы. Направленность к центру сферы очевидна из
симметрии задачи, а то, что действие такое же, как от точечной массы, помещенной в
центре, можно получить простым интегрированием. до центра сферы. Направленность к центру сферы очевидна из
симметрии задачи, а то, что действие такое же, как от точечной массы, помещенной в
центре, можно получить простым интегрированием.
Рассмотрим звезду радиуса 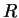 c переменной плотностью c переменной плотностью  и полной массой и полной массой
 Полная сила, действующая на пробную частицу при
Полная сила, действующая на пробную частицу при  равна равна
 но внутри звезды (
но внутри звезды ( ) )
 Величину
Величину
 обычно называют текущей массой.
Величина обычно называют текущей массой.
Величина 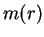 естественно появляется при рассмотрении равновесия звезд. естественно появляется при рассмотрении равновесия звезд.
Решение нестационарных задач сжатия звезд, как и любых гидродинамических задач,
можно проводить двумя способами. Выбирая в качестве независимых переменных
координату  и время и время 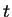 , можно рассматривать изменения физических величин
(плотности, давления и т.д.) в какой-либо фиксированной точке пространства
(эйлеров подход). Но часто бывает удобно следить за поведением выбранных заранее
частиц вещества (лагранжев подход), в этом случае независимыми переменными
являются начальные координаты , можно рассматривать изменения физических величин
(плотности, давления и т.д.) в какой-либо фиксированной точке пространства
(эйлеров подход). Но часто бывает удобно следить за поведением выбранных заранее
частиц вещества (лагранжев подход), в этом случае независимыми переменными
являются начальные координаты  и время и время 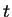 , а координата , а координата  является функцией
является функцией  . Лагранжев подход чаще всего осуществляется в задачах,
обладающих какой-либо симметрией движений, например, при сферически-симметричном
расширении (или сжатии) звезды. Зададим в начальный момент в качестве лагранжевой
координаты расстояние до центра звезды . Лагранжев подход чаще всего осуществляется в задачах,
обладающих какой-либо симметрией движений, например, при сферически-симметричном
расширении (или сжатии) звезды. Зададим в начальный момент в качестве лагранжевой
координаты расстояние до центра звезды  . Сфера с радиусом . Сфера с радиусом  содержит
вполне определенную часть массы звезды содержит
вполне определенную часть массы звезды  , величина которой при сферических
движениях не меняется со временем. В этом случае текущая масса , величина которой при сферических
движениях не меняется со временем. В этом случае текущая масса 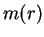 может быть
выбрана в качестве независимой (лагранжевой) координаты. может быть
выбрана в качестве независимой (лагранжевой) координаты.
Рассмотрим несколько примеров:
 |
| Рис. 4. |
1. Шар радиуса 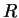 имеет постоянную плотность имеет постоянную плотность 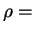 const. Очевидно, что решение
уравнения (1.1) имеет вид const. Очевидно, что решение
уравнения (1.1) имеет вид
 const const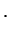 Подставляя это решение в уравнение
(1.1), получим
Подставляя это решение в уравнение
(1.1), получим
 и найдем, что
и найдем, что
 const const Снаружи, при
Снаружи, при  , имеем , имеем
 . Значение const находим из условия
непрерывности потенциала при . Значение const находим из условия
непрерывности потенциала при  (см. рис. 4)
(производные при этом сшиваются
автоматически):
(см. рис. 4)
(производные при этом сшиваются
автоматически):
 const const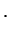 Учтем, что
Учтем, что
 , и получим , и получим
 при при
2. Теперь предположим, что
 (
(
 -- дельта-функция Дирака), т.е. -- дельта-функция Дирака), т.е.  при при  и и  , а масса , а масса
 Очевидно, что
Очевидно, что 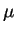 имеет смысл поверхностной плотности (размерность имеет смысл поверхностной плотности (размерность ![$ [\mu]=$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img114.gif) г/см г/см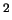 ).
Поскольку ).
Поскольку
 внутри сферы внутри сферы 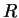 , ясно, что , ясно, что  const при const при  .
Снаружи по-прежнему .
Снаружи по-прежнему
 . Сшивая потенциал при . Сшивая потенциал при  , получим
(рис. 5) , получим
(рис. 5)

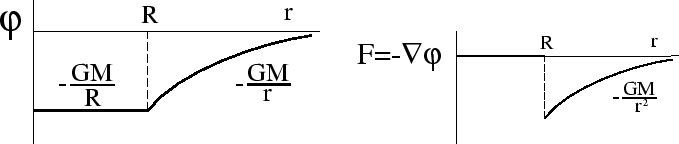 |
| Рис. 5. | Рис. 6. |
Мы видим, что в этом случае
 имеет разрыв
(рис. 6). Можно показать,
что этот результат совершенно общий: конечная масса, сосредоточенная в бесконечно
тонком слое с конечной поверхностью, дает разрыв нормальной производной потенциала: имеет разрыв
(рис. 6). Можно показать,
что этот результат совершенно общий: конечная масса, сосредоточенная в бесконечно
тонком слое с конечной поверхностью, дает разрыв нормальной производной потенциала:

3. Дано:
 . Чему равно . Чему равно
 ? Непосредственное вычисление
производных дает нуль везде, за исключением точки ? Непосредственное вычисление
производных дает нуль везде, за исключением точки  . В самом деле . В самом деле
 и легко убедимся, что
и легко убедимся, что
 , кроме , кроме  , где имеем неопределенность 0/0. , где имеем неопределенность 0/0.
Еще проще в данном случае вычисление в сферических координатах. Для потенциала, не
зависящего от угла
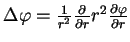 , и подставляя , и подставляя
 , снова получим , снова получим
 . Однако неправильно было бы отвечать, что везде . Однако неправильно было бы отвечать, что везде
 .
Такой ответ не верен, так как поток .
Такой ответ не верен, так как поток
 через любую поверхность, окружающую
начало координат, отличен от нуля и равен через любую поверхность, окружающую
начало координат, отличен от нуля и равен  . Правильный ответ: . Правильный ответ:
 Здесь
Здесь
 -- трехмерная дельта-функция Дирака. Таким образом, отвечая,
что -- трехмерная дельта-функция Дирака. Таким образом, отвечая,
что
 , нужно добавить: везде, кроме начала координат, где вторые
производные от , нужно добавить: везде, кроме начала координат, где вторые
производные от 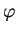 стремятся к бесконечности. стремятся к бесконечности.
4. Рассмотрим теперь общий случай сферически-симметричного распределения плотности
 . Определим, как раньше, текущую массу . Определим, как раньше, текущую массу
 Интегрируя уравнение Пуассона, последовательно получим
Интегрируя уравнение Пуассона, последовательно получим
 Cмысл полученного выражения для
Cмысл полученного выражения для 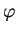 легко понять. Первый член -- это потенциал
сферически-симметричной массы, расположенной внутри сферы радиуса легко понять. Первый член -- это потенциал
сферически-симметричной массы, расположенной внутри сферы радиуса 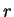 . Второй член
является суммой потенциалов от внешних слоев. . Второй член
является суммой потенциалов от внешних слоев.
C учетом соотношения для 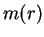 запишем выражение для потенциала в виде запишем выражение для потенциала в виде
 В последнем интеграле мы заменили верхний предел
В последнем интеграле мы заменили верхний предел 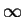 на на 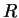 , предполагая, что
при , предполагая, что
при  плотность плотность  . .
<< 1.2 Векторное поле ускорений ...
| Оглавление |
1.4 Энергия гравитационного взаимодействия >>
Посмотреть комментарии[2]
|

