<< 9.1 Решение Шварцшильда
| Оглавление |
9.3 Сферически-симметричное поле ... >>
Теперь рассмотрим движение частиц в этом поле. По ньютоновской теории для частиц,
покоящихся на бесконечности, используя закон сохранения энергии, имеем
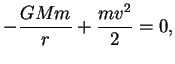 т. е.
т. е.
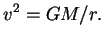 Определим наивно
Определим наивно 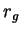 как радиус, где как радиус, где 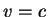 . Тогда (ср. раздел 1.7) . Тогда (ср. раздел 1.7)
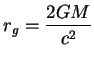 Этот результат получил еще Лаплас. Подчеркнем, однако, что это не больше чем
мнемонический прием. Очевидно, что ньютоновская механика неприменима при
Этот результат получил еще Лаплас. Подчеркнем, однако, что это не больше чем
мнемонический прием. Очевидно, что ньютоновская механика неприменима при 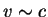 . .
Теперь напишем строго уравнение движения частиц в поле Шварцшильда. В метрике,
не зависящей от времени, сохраняется энергия, т. е. компонента 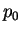 (именно с нижним
индексом) 4-вектора импульса частицы: (именно с нижним
индексом) 4-вектора импульса частицы:
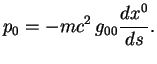 В статическом поле
В статическом поле
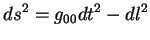 или
или
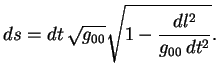 Величина
Величина
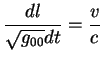 это скорость, измеренная локальным наблюдателем. Тогда имеем
это скорость, измеренная локальным наблюдателем. Тогда имеем
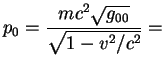 const const (это соотношение не зависит от направления
(это соотношение не зависит от направления 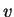 ). ).
Пусть при
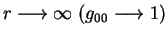
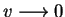 ,
т.е. ,
т.е. 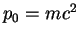 . В этом случае всегда . В этом случае всегда
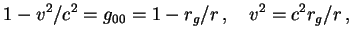 т.е. в ОТО имеет место связь между
т.е. в ОТО имеет место связь между 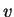 и и 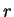 в точности такая, как в ньютоновской механике
и теории тяготения. В частности, в точности такая, как в ньютоновской механике
и теории тяготения. В частности, 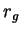 -- это как раз тот радиус, где -- это как раз тот радиус, где 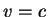 , если
при , если
при
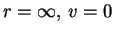 в такой теории. Если в такой теории. Если 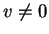 на бесконечности, то на бесконечности, то
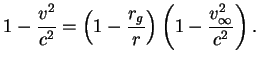 Таким образом, в точной теории в ОТО
Таким образом, в точной теории в ОТО 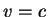 только на только на 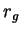 независимо9.1 от значения независимо9.1 от значения
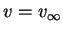 при при
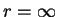 . .
Еще раз подчеркнем, что 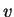 -- это скорость, измеренная локальным наблюдателем. -- это скорость, измеренная локальным наблюдателем.
В дальнейшем положим 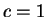 . При движении по радиусу в случае . При движении по радиусу в случае 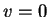 при при
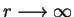
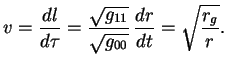 Тогда, используя выражение для
Тогда, используя выражение для 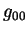 и и 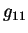 , ,
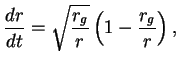
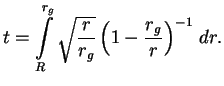 При падении с конечного
При падении с конечного 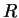 этот интеграл логарифмически расходится при этот интеграл логарифмически расходится при
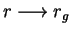 . Отметим, что . Отметим, что 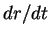 проходит через максимум и стремится к нулю при проходит через максимум и стремится к нулю при
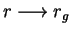 . Конечно, в шварцшильдовском поле нет отталкивания, хотя . Конечно, в шварцшильдовском поле нет отталкивания, хотя
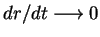 при
при
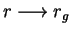 , так как , так как 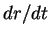 -- это не скорость. -- это не скорость.
Существует хорошее сравнение. Если мы будем бросать частицы на черную дыру, то мы
увидим, что они замедляют движение и скучиваются вблизи 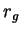 . Эта остановка не
соответствует положению равновесия. Представим себе, что снимается на кинопленку
прыгун, а потом при просмотре замедляется скорость движения пленки, так что в некоторый момент
он остановится. То же самое при движении частиц. Если установить часы на частицах, которые
действительно останавливаются в положении равновесия, то часы все равно идут. В
случае дыры частицы останавливаются, но останавливаются и часы на них. По собственному
времени никаких остановок не происходит. Просто с точки зрения удаленного наблюдателя
часы замедляются из-за доплер-эффекта и из-за влияния гравитационного потенциала. . Эта остановка не
соответствует положению равновесия. Представим себе, что снимается на кинопленку
прыгун, а потом при просмотре замедляется скорость движения пленки, так что в некоторый момент
он остановится. То же самое при движении частиц. Если установить часы на частицах, которые
действительно останавливаются в положении равновесия, то часы все равно идут. В
случае дыры частицы останавливаются, но останавливаются и часы на них. По собственному
времени никаких остановок не происходит. Просто с точки зрения удаленного наблюдателя
часы замедляются из-за доплер-эффекта и из-за влияния гравитационного потенциала.
Представим себе падение газа, состоящего из отдельных частиц с точки зрения далекого
наблюдателя.
Оказывается, что газ скапливается вблизи 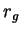 , но не отдает свою кинетическую энергию.
Несмотря на то, что количество скопившегося газа неограниченно возрастает с течением времени, его плотность,
измеренная в собственной системе (наблюдателя, движущегося вместе с газом), остается
конечной в каждой точке пространства, в частности вблизи , но не отдает свою кинетическую энергию.
Несмотря на то, что количество скопившегося газа неограниченно возрастает с течением времени, его плотность,
измеренная в собственной системе (наблюдателя, движущегося вместе с газом), остается
конечной в каждой точке пространства, в частности вблизи 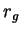 . .
Задача. Рассчитать радиальное движение для света (фотонов) в метрике Шварцшильда.
<< 9.1 Решение Шварцшильда
| Оглавление |
9.3 Сферически-симметричное поле ... >>
Посмотреть комментарии[2]
|

