<< 8.3 Физика искривленного ...
| Оглавление |
9. Сильные гравитационные поля ... >>
В предыдущих разделах мы увидели, что основная идея ОТО о движении тел в искривленном
пространстве-времени по геодезическим означает, что все тела падают в гравитационном поле
по одинаковым траекториям с одинаковым ускорением.

|
| Рис. 53. |
Покажем сейчас с помощью ОТО и квантовой механики, что в гравитационном поле происходит
замедление времени. Для этого рассмотрим один проект вечного двигателя. На установке из двух
блоков (рис. 53)
будем поднимать ядра дейтерия, а опускать протоны и нейтроны.
Пусть внизу протоны реагируют с нейтронами, а образующиеся 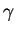 -кванты
используются наверху для диссоциации дейтерия. Масса -кванты
используются наверху для диссоциации дейтерия. Масса 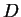 на 2,2 МэВ меньше на 2,2 МэВ меньше  ,
поэтому под действием большей тяжести p-n система будет отдавать энергию, совершать
вечное движение. ,
поэтому под действием большей тяжести p-n система будет отдавать энергию, совершать
вечное движение.
Ошибка этого проекта в том, что в действительности 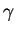 -квант не поглотится, так как
часть его энергии уйдет на преодоление силы тяжести: -квант не поглотится, так как
часть его энергии уйдет на преодоление силы тяжести:
 Энергия
Энергия 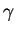 -кванта -кванта
 . Поскольку . Поскольку
 ,
то ,
то
 , т. е. частота фотонов испытывает красное смещение в гравитационном поле.
Этот эффект уже наблюдался на Земле с помощью эффекта Мессбауэра (опыт Паунда и Ребки). , т. е. частота фотонов испытывает красное смещение в гравитационном поле.
Этот эффект уже наблюдался на Земле с помощью эффекта Мессбауэра (опыт Паунда и Ребки).
В общем случае можно написать
 где
где
 -- различие гравитационного потенциала в
местах испускания и приема. Это соотношение верно для фотонов
любых частот. В данном месте частота фотонов зависит только от
свойств испускающих их атомов (или ядер). На этих же свойствах
основано и измерение времени в данном месте (атомные часы).
Поэтому наблюдатель, находящийся в точке с другим гравитационным
потенциалом, будет интерпретировать сдвиг частот как изменение
хода времени: -- различие гравитационного потенциала в
местах испускания и приема. Это соотношение верно для фотонов
любых частот. В данном месте частота фотонов зависит только от
свойств испускающих их атомов (или ядер). На этих же свойствах
основано и измерение времени в данном месте (атомные часы).
Поэтому наблюдатель, находящийся в точке с другим гравитационным
потенциалом, будет интерпретировать сдвиг частот как изменение
хода времени:
 |
(8.2) |

|
| Рис. 54. |
Раньше мы говорили об изменении в гравитационном поле метрики вообще, а теперь
видим более конкретно, что изменяется течение времени в разных точках. Это можно интерпретировать
как изменение коэффициента 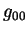 при временной координате в метрике. Рассмотрев как изменяется при временной координате в метрике. Рассмотрев как изменяется
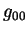 в слабом поле (т. е. ньютоновском случае), мы увидим, что в слабом поле (т. е. ньютоновском случае), мы увидим, что 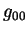 играет
роль ньютоновского потенциала для медленных частиц. играет
роль ньютоновского потенциала для медленных частиц.
Рассмотрим статическое гравитационное поле. По определению это значит, что метрику
можно написать в виде
 причем ни
причем ни 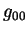 , ни , ни
 не зависят от временной координаты не зависят от временной координаты  .
Пусть в некоторой точке .
Пусть в некоторой точке  испускаются два световых сигнала с запаздыванием испускаются два световых сигнала с запаздыванием
 и принимаются в точке
и принимаются в точке  (см. рис. 54).
Поскольку (см. рис. 54).
Поскольку 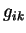 от от  не зависит, мировая
линия второго сигнала отличается от первой только сдвигом по координате не зависит, мировая
линия второго сигнала отличается от первой только сдвигом по координате  на на
 , т. е. запаздывание сигналов в точке приема по координатному времени
тоже будет , т. е. запаздывание сигналов в точке приема по координатному времени
тоже будет
 .
Однако наблюдатель пользуется не координатным, а собственным временем .
Однако наблюдатель пользуется не координатным, а собственным временем 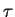 .
Это соответствует тому, что он в своей окрестности пользуется метрикой .
Это соответствует тому, что он в своей окрестности пользуется метрикой
 Интервал между двумя событиями -- приходом сигналов в точку
Интервал между двумя событиями -- приходом сигналов в точку  -- инвариантен
(не зависит от выбора метрики), т. е. -- инвариантен
(не зависит от выбора метрики), т. е.
 Отсюда и из (8.2) получаем связь
Отсюда и из (8.2) получаем связь 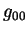 и ньютоновского потенциала и ньютоновского потенциала 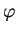 : :

<< 8.3 Физика искривленного ...
| Оглавление |
9. Сильные гравитационные поля ... >>
Посмотреть комментарии[2]
|

